【机器学习系列2】FPGrowth算法与spark实现

原理

基础

支持度

支持度是指在所有项集中{X, Y}出现的可能性，即项集中同时含有X和Y的概率： 该指标作为建立强关联规则的第一个门槛，衡量了所考察关联规则在“量”上的多少。

置信度

置信度表示在先决条件X发生的条件下，关联结果Y发生的概率： 这是生成强关联规则的第二个门槛，衡量了所考察的关联规则在“质”上的可靠性。

提升度

提升度表示在含有X的条件下同时含有Y的可能性与没有X这个条件下项集中含有Y的可能性之比，该指标与置信度同样衡量规则的可靠性，可以看作是置信度的一种互补指标。

FPGrowth算法

FP-Growth(频繁模式增长)算法是韩家炜在2000年提出的关联分析算法，它采取如下分治策略：将提供频繁项集的数据库压缩到一棵频繁模式树（FP-Tree），但仍保留项集关联信息

该算法和Apriori算法最大的不同有两点：

第一，不产生候选集，

第二，只需要两次遍历数据库，大大提高了效率。

FP数构造

事务数据库建立（很关键）

注意：

许多项集有公共项，而且出现次数越多的项越可能是公共项，因此按出现次数由多到少的顺序可以节省空间，实现压缩存储。

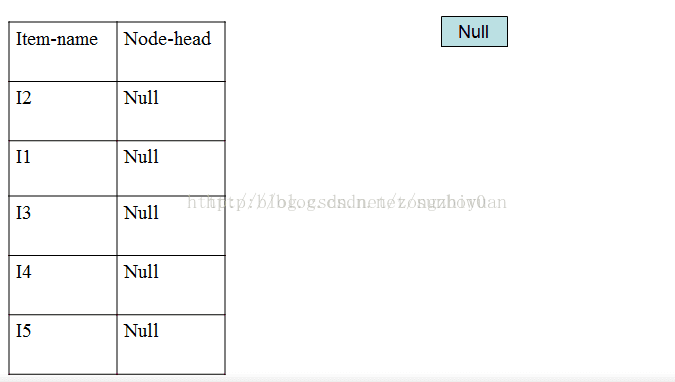
创建根结点和频繁项目表

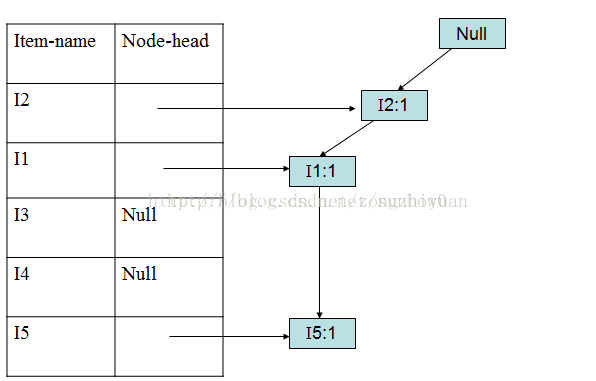
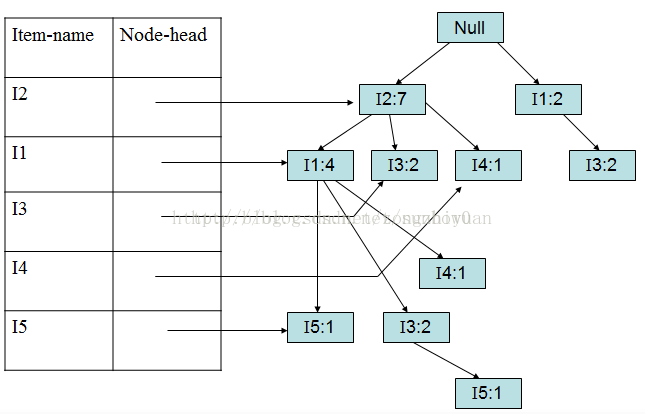
加入第一个事务(I2,I1,I5)

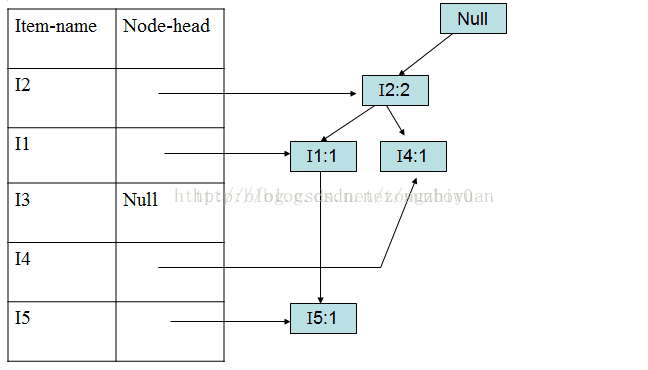
加入第二个事务(I2,I4)

加入第三个事务(I2,I3)

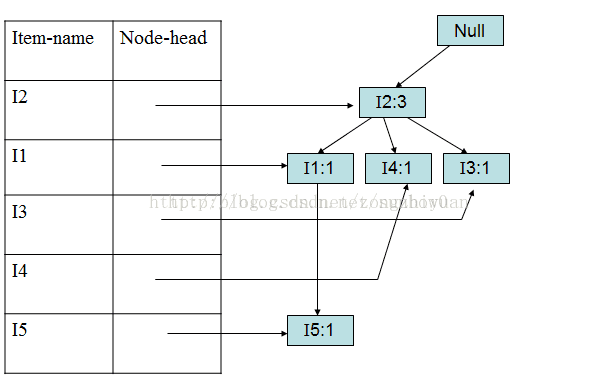
以此类推加入第5、6、7、8、9个事务。

加入第九个事务(I2,I1,I3)

FP数挖掘

FpTree建好后，就可以进行频繁项集的挖掘，挖掘算法称为FpGrowth（Frequent Pattern Growth）算法。

挖掘从表头header的最后一个项开始，以此类推。下面以I5、I3为例进行挖掘

对于I5，得到条件模式基：<(I2,I1:1)>、

构造条件FP-tree：

得到I5频繁项集：{{I2,I5:2},{I1,I5:2},{I2,I1,I5:2}}

I5的情况是比较简单的，因为I5对应的条件FP-树是单路径的，I3稍微复杂一点。I3的条件模式基是(I2 I1:2), (I2:2),(I1:2)，生成的条件FP-树如下图：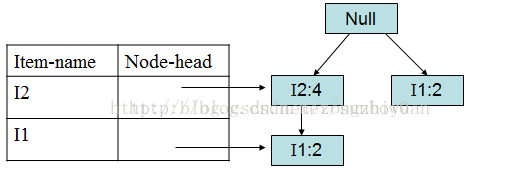

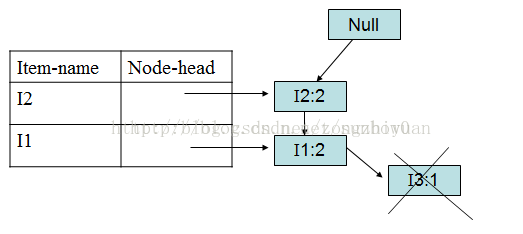
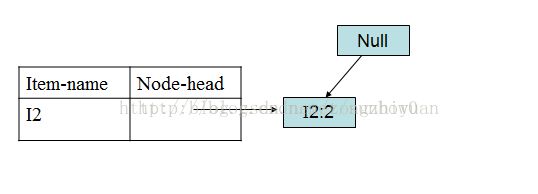
I3的条件FP-树仍然是一个多路径树，首先把模式后缀I3和条件FP-树中的项头表中的每一项取并集，得到一组模式{I2 I3:4, I1 I3:4}，但是这一组模式不是后缀为I3的所有模式。还需要递归调用FP-growth，模式后缀为{I1，I3}，{I1，I3}的条件模式基为{I2：2}，其生成的条件FP-树如下图所示。

在FP_growth中把I2和模式后缀{I1，I3}取并得到模式{I1 I2 I3：2}。 理论上还应该计算一下模式后缀为{I2，I3}的模式集，但是{I2，I3}的条件模式基为空，递归调用结束。最终模式后缀I3的支持度>2的所有模式为：{ I2 I3:4, I1 I3:4, I1 I2 I3:2}。

Spark实现

FPGrowth源码包括：FPGrowth、FPTree两部分。 其中FPGrowth中包括：run方法、genFreqItems方法、genFreqItemsets方法、genCondTransactions方法； FPTree中包括：add方法、merge方法、project方法、getTransactions方法、extract方法。

// run 计算频繁项集
 /**
   * Computes an FP-Growth model that contains frequent itemsets.
   * @param data input data set, each element contains a transaction
   * @return an [[FPGrowthModel]]
   */
  def run[Item: ClassTag](data: RDD[Array[Item]]): FPGrowthModel[Item] = {
    if (data.getStorageLevel == StorageLevel.NONE) {
      logWarning("Input data is not cached.")
    }
    val count = data.count()//计算事务总数
    val minCount = math.ceil(minSupport * count).toLong//计算最小支持度
    val numParts = if (numPartitions > 0) numPartitions else data.partitions.length
    val partitioner = new HashPartitioner(numParts)
    //freqItems计算满足最小支持度的Items项
    val freqItems = genFreqItems(data, minCount, partitioner)
    //freqItemsets计算频繁项集
    val freqItemsets = genFreqItemsets(data, minCount, freqItems, partitioner)
    new FPGrowthModel(freqItemsets)
}
// genFreqItems计算满足最小支持度的Items项(并且排序)
 /**
   * Generates frequent items by filtering the input data using minimal support level.
   * @param minCount minimum count for frequent itemsets
   * @param partitioner partitioner used to distribute items
   * @return array of frequent pattern ordered by their frequencies
   */
  private def genFreqItems[Item: ClassTag](
      data: RDD[Array[Item]],
      minCount: Long,
      partitioner: Partitioner): Array[Item] = {
    data.flatMap { t =>
      val uniq = t.toSet
      if (t.size != uniq.size) {
        thrownew SparkException(s"Items in a transaction must be unique but got ${t.toSeq}.")
      }
      t
    }.map(v => (v, 1L))
      .reduceByKey(partitioner, _ + _)
      .filter(_._2 >= minCount)
      .collect()
      .sortBy(-_._2)
      .map(_._1)
    }//统计每个Items项的频次，对小于minCount的Items项过滤，返回Items项。

// genFreqItemsets计算频繁项集：生成FP-Trees，挖掘FP-Trees
 /**
   * Generate frequent itemsets by building FP-Trees, the extraction is done on each partition.
   * @param data transactions
   * @param minCount minimum count for frequent itemsets
   * @param freqItems frequent items
   * @param partitioner partitioner used to distribute transactions
   * @return an RDD of (frequent itemset, count)
   */
  private def genFreqItemsets[Item: ClassTag](
      data: RDD[Array[Item]],
      minCount: Long,
      freqItems: Array[Item],
      partitioner: Partitioner): RDD[FreqItemset[Item]] = {
    val itemToRank = freqItems.zipWithIndex.toMap//表头
    data.flatMap { transaction =>
      genCondTransactions(transaction, itemToRank, partitioner)
    }.aggregateByKey(new FPTree[Int], partitioner.numPartitions)( //生成FP树
      (tree, transaction) => tree.add(transaction, 1L), //FP树增加一条事务
      (tree1, tree2) => tree1.merge(tree2)) //FP树合并
    .flatMap { case (part, tree) =>
      tree.extract(minCount, x => partitioner.getPartition(x) == part)//FP树挖掘频繁项
    }.map { case (ranks, count) =>
      new FreqItemset(ranks.map(i => freqItems(i)).toArray, count)
    }
}
// add FP-Trees增加一条事务数据
/** Adds a transaction with count. */
  def add(t: Iterable[T], count: Long = 1L): this.type = {
    require(count > 0)
    var curr = root
    curr.count += count
    t.foreach { item =>
      val summary = summaries.getOrElseUpdate(item, new Summary)
      summary.count += count
      val child = curr.children.getOrElseUpdate(item, {
        val newNode = new Node(curr)
        newNode.item = item
        summary.nodes += newNode
        newNode
      })
      child.count += count
      curr = child
    }
    this
}
// merge FP-Trees合并
  /** Merges another FP-Tree. */
  def merge(other: FPTree[T]): this.type = {
    other.transactions.foreach { case (t, c) =>
      add(t, c)
    }
    this
}
// extract FP-Trees挖掘，返回所有频繁项集
  /** Extracts all patterns with valid suffix and minimum count. */
  def extract(
      minCount: Long,
      validateSuffix: T => Boolean = _ => true): Iterator[(List[T], Long)] = {
    summaries.iterator.flatMap { case (item, summary) =>
      if (validateSuffix(item) && summary.count >= minCount) {
        Iterator.single((item :: Nil, summary.count)) ++
          project(item).extract(minCount).map { case (t, c) =>
            (item :: t, c)
          }
      } else {
        Iterator.empty
      }
    }
  }
}

注意事项

FpGrowth算法的平均效率远高于Apriori算法，但是它并不能保证高效率，它的效率依赖于数据集，当数据集中的频繁项集没有公共项时，所有的项集都挂在根结点上，不能实现压缩存储，而且Fptree还需要其他的开销，需要存储空间更大，使用FpGrowth算法前，对数据分析一下，看是否适合用FpGrowth算法。

参考：

https://my.oschina.net/u/1244232/blog/525321?from=groupmessage&isappinstalled=0

Han jia wei, Pei Jan等 Mining Frequent Patterns without Candidate Generation: A Frequent-Pattern Tree Approach.2004