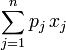背包问题
背包问题(Knapsack problem)是一种组合优化的NP完全问题。问题可以描述为:给定一组物品,每种物品都有自己的重量和价格,在限定的总重量内,我们如何选择,才能使得物品的总价格最高。问题的名称来源于如何选择最合适的物品放置于给定背包中。
相似问题经常出现在商业、组合数学,计算复杂性理论、密码学和应用数学等领域中。
也可以将背包问题描述为决定性问题,即在总重量不超过W的前提下,总价值是否能达到V?
目录[隐藏]
|
[编辑]定义
我们有n种物品,物品j的重量为wj,价格为pj。我们假定所有物品的重量和价格都是非负的。背包所能承受的最大重量为W。
如果限定每种物品只能选择0个或1个,则问题称为0-1背包问题。可以用公式表示为:
如果限定物品j最多只能选择bj个,则问题称为有界背包问题。可以用公式表示为:
如果不限定每种物品的数量,则问题称为无界背包问题。
各类复杂的背包问题总可以变换为简单的0-1背包问题进行求解。
[编辑]计算复杂度
在计算机科学领域,人们对背包问题感兴趣的原因在于:
- 利用动态规划,背包问题存在一个伪多项式时间算法
- 把上面算法作为子程序,背包问题存在完全逼近多项式时间方案
- 作为NP完全问题,背包问题没有一种既准确又快速(多项式时间)的算法
[编辑]动态规划解法
[编辑]无界背包问题
如果重量w1, ..., wn和W都是非负的整数,那么用动态规划,可以用伪多项式时间解决背包问题。下面描述了无界背包问题的解法。
简便起见,我们假定重量都是正整数(wj > 0)。在总重量不超过W的前提下,我们希望总价格最高。对于Y ≤W,我们将在总重量不超过Y的前提下,总价格所能达到的最高值定义为A(Y)。A(W)即为问题的答案。
显然,A(Y)满足:
- A(0) = 0
- A(Y) = max { A(Y - 1), max { pj +A(Y -wj) |wj ≤Y } }
其中,pj为第j种物品的价格。
关于第二个公式的一个解释:总重量为Y时背包的最高价值可能有两种情况,第一种是该重量无法被完全填满,这对应于表达式A(Y - 1)。第二种是刚好填满,这对应于一个包含一系列刚好填满的可能性的集合,其中的可能性是指当最后放进包中的物品恰好是重量为wj的物品时背包填满并达到最高价值。而这时的背包价值等于重量为wj物品的价值和当没有放入该物品时背包的最高价值之和。故归纳为表达式pj + A(Y - wj)。最后把所有上述情况中背包价值的最大值求出就得到了A(Y)的值。
如果总重量为0,总价值也为0。然后依次计算A(0), A(1), ..., A(W),并把每一步骤的结果存入表中供后续步骤使用,完成这些步骤后A(W)即为最终结果。由于每次计算A(Y)都需要检查n种物品,并且需要计算W个A(Y)值,因此动态规划解法的时间复杂度为O(nW)。如果把w1, ..., wn, W都除以它们的最大公因数,算法的时间将得到很大的提升。
尽管背包问题的时间复杂度为O(nW),但它仍然是一个NP完全问题。这是因为W同问题的输入大小并不成线性关系。原因在于问题的输入大小仅仅取决于表达输入所需的比特数。事实上,logW,即表达W所需的比特数,同问题的输入长度成线性关系。
[编辑]0-1背包问题
类似的方法可以解决0-1背包问题,算法同样需要伪多项式时间。我们同样假定w1, ...,wn和W都是正整数。我们将在总重量不超过Y的前提下,前j种物品的总价格所能达到的最高值定义为A(j,Y)。
A(j, Y)的递推关系为:
- A(0, Y) = 0
- A(j, 0) = 0
- 如果wj > Y, A(j, Y) = A(j - 1, Y)
- 如果wj ≤ Y, A(j, Y) = max { A(j - 1, Y), pj + A(j - 1,Y -wj) }
通过计算A(n, W)即得到最终结果。为提高算法性能,我们把先前计算的结果存入表中。因此算法需要的时间和空间都为O(nW),通过对算法的改进,空间的消耗可以降至O(W)。
[编辑]二次背包问题
推广的背包问题有二次背包问题,多维背包问题,多目标背包问题等。
二次背包问题是背包问题的一种推广形式:
maximize 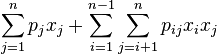 |
|||
| subject to | 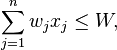 |
||
| for all |
|||
[编辑]外部链接
- 二次背包问题源代码链接
程序实现:
/*
假設有一個背包的負重最多可達8公斤,而希望在背包中裝入
負重範圍內可得之總價物品,假設是水果好了,水果的編號、單價與重量
*/
#include
#include
#include
#define N 5 //物品种类
#define MIN 1 //最小重量
#define LIMIT 8 //重量限制
using namespace std;
struct body
{
char name[20];
int size;
int price;
};
int main()
{
int item[LIMIT+1]={0};//value表示目前的最佳解所得之總價
int value[LIMIT+1]={0};//item表示最後一個放至背包的水果
body a[]= {{"李子", 4, 4500},
{"蘋果", 5, 5700},
{"橘子", 2, 2250},
{"草莓", 1, 1100},
{"甜瓜", 6, 6700}};
int i,s;
for(i=0;ivalue[s])
{
value[s]=newValue;
item[s]=i;
}
}
}
printf("物品\t价格\n");
for(i=LIMIT;i>=MIN;i=i-a[item[i]].size)
{
printf("%s\t%d\n",a[item[i]].name, a[item[i]].price);
}
printf("合計\t%d\n", value[LIMIT]);
return 0;
}