LeetCode 部分题笔记

 

一、动态规划

11. 盛最多水的容器

→_→

给定 n 个非负整数 a1，a2，…，an，每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。
说明：你不能倾斜容器，且 n 的值至少为 2。
示例:
输入: [1,8,6,2,5,4,8,3,7]
输出: 49

双指针法：每次较小的指针向中间移（如果移动较大的，容积只减不增）

class Solution:
    def maxArea(self, height: List[int]) -> int:
        left = 0
        right = len(height) - 1
        maxarea = min(height[left], height[right]) * right
        while left + 1 < right:
            if height[left] <= height[right]:
                left += 1
            else:
                right -= 1
            maxarea = max(maxarea, min(height[left], height[right]) * (right - left))
        return maxarea

 

53. 最大子序和

→_→

给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。
示例:
输入: [-2,1,-3,4,-1,2,1,-5,4],
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。

解法一：递归。首先遍历累加，若累加到第k个数时和小于0，则可将列表一分为二（前k个和k之后）分别找最大连续子数组。累加的时候已找到前一半的子数组最大和，后一半递归

class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        s = 0
        m = nums[0]
        for i in range(len(nums)):
            s += nums[i]
            if s < 0 and i != len(nums) - 1:
                return max(m, self.maxSubArray(nums[i + 1:]))
            m = max(m, s)
        return m

解法二：动态规划，定义一个函数 $f(n)$ ，表示以第$n$个数为结束点的子数列的最大和，则存在递推关系 $f(n)=\max (f(n-1)+A[n],A[n])$ 。时间上与递归差不多，占用内存小于递归。

class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        if not nums:
            return 0
        f = nums[0]
        m = f
        for i in range(1, len(nums)):
            f = max(f + nums[i], nums[i])
            m = max(m, f)
        return m

 

62. 不同路径

→_→

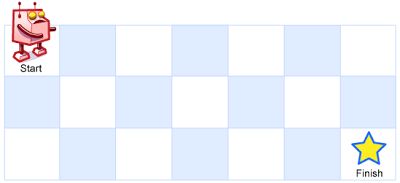
一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。
问总共有多少条不同的路径？
例如，上图是一个7 x 3 的网格。有多少可能的路径？
说明：m 和 n 的值均不超过 100。

法一：动态规划法，当 $m,n>1$ 时$f(m,n)=f(m-1,n)+f(m,n-1)$ ， $f(1,n)=f(m,1)=1$ 。时间复杂度：$O(mn)$

class Solution:
    def uniquePaths(self, m: int, n: int) -> int:
        matrix = [[1] * n] * m 
        for i in range(1, m):
            for j in range(1, n):
                matrix[i][j] = matrix[i - 1][j] + matrix[i][j - 1]
        return matrix[m - 1][n - 1]

法二：数学法，机器人要走$m+n-2$步，即从$m+n-2$中挑出$m-1$步向下走，即 $C_{m+n-2}^{m-1}$。时间复杂度：$O(\min (m,n))$ 。

class Solution:
    def uniquePaths(self, m: int, n: int) -> int:
        a = m + n - 2
        b = min(m, n) - 1
        res = 1
        for i in range(b):
            res *= (a - i) / (i + 1)
        return int(res)

 

121. 买卖股票的最佳时机

→_→

给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格。
如果你最多只允许完成一笔交易（即买入和卖出一支股票），设计一个算法来计算你所能获取的最大利润。
注意你不能在买入股票前卖出股票。
示例 1:
输入: [7,1,5,3,6,4]
输出: 5
解释: 在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。

动态规划，设 $f(n)$ 表示前 $n$ 天的最大收益，那么 $f(0)=0$，$f(k)=\max (f(k-1),第k天的价格-前k-1天中最小价格)$

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        min_price = prices[0] if prices else 0
        res = 0
        for i in range(1, len(prices)):
            min_price = min(min_price, prices[i])
            res = max(res, prices[i] - min_price)
        return res

 

329. 矩阵中的最长递增路径（困难）

→_→

给定一个整数矩阵，找出最长递增路径的长度。
对于每个单元格，你可以往上，下，左，右四个方向移动。 你不能在对角线方向上移动或移动到边界外（即不允许环绕）。
示例 1:
输入: nums =
[
[9,9,4],
[6,6,8],
[2,1,1]
]
输出: 4
解释: 最长递增路径为 [1, 2, 6, 9]。
示例 2:
输入: nums =
[
[3,4,5],
[3,2,6],
[2,2,1]
]
输出: 4
解释: 最长递增路径是 [3, 4, 5, 6]。注意不允许在对角线方向上移动。

动态规划，先将每个对$(i,j)$按照$matrix(i,j)$从小到大排序存入path，用一个矩阵num1保存暂时的每个元素为终点的最大递增路径长度，然后对path中的每个值（即矩阵中的每个元素从小到大），如果$(i,j)$的上下左右有比$matrix(i,j)$小的，那么将这些比它小的元素对应的num1位置上的最大的那个值+1赋值给$num1(i,j)$，最终矩阵num1中最大的元素即为最长递增路径。

class Solution:
    def longestIncreasingPath(self, matrix: List[List[int]]) -> int:
        m = len(matrix)
        if not m:
            return 0
        dic = {}
        ret = 1
        n = len(matrix[0])
        for i in range(m):
            for j in range(n):
                dic[(i, j)] = matrix[i][j]
        v = dic.keys()
        nums1 = [[1 for _ in range(n)] for _ in range(m)]
        path = sorted(dic.items(), key=lambda x: x[1])
        print(path)
        for k, _ in path:
            i = k[0]
            j = k[1]
            if (i + 1, j) in v and matrix[i + 1][j] < matrix[i][j] and nums1[i][j] < nums1[i + 1][j] + 1:
                nums1[i][j] = nums1[i + 1][j] + 1
            if (i, j + 1) in v and matrix[i][j + 1] < matrix[i][j] and nums1[i][j] < nums1[i][j + 1] + 1:
                nums1[i][j] = nums1[i][j + 1] + 1
            if (i - 1, j) in v and matrix[i - 1][j] < matrix[i][j] and nums1[i][j] < nums1[i - 1][j] + 1:
                nums1[i][j] = nums1[i - 1][j] + 1
            if (i, j - 1) in v and matrix[i][j - 1] < matrix[i][j] and nums1[i][j] < nums1[i][j - 1] + 1:
                nums1[i][j] = nums1[i][j - 1] + 1
            ret = max(ret, nums1[i][j])
        return ret

 

10. 正则表达式匹配

→_→

给你一个字符串 s 和一个字符规律 p，请你来实现一个支持 ‘.’ 和 ‘*’ 的正则表达式匹配。
‘.’ 匹配任意单个字符
‘*’ 匹配零个或多个前面的那一个元素
所谓匹配，是要涵盖 整个 字符串 s的，而不是部分字符串。

说明:
s 可能为空，且只包含从 a-z 的小写字母。
p 可能为空，且只包含从 a-z 的小写字母，以及字符 . 和 *。

• 递归法

class Solution:
    def isMatch(self, s: str, p: str) -> bool:
        if not p and not s:
            return True
        if not p and s:
            return False
        if not s:
            if p[-1] == '*':
                return self.isMatch(s, p[:-2])
            else:
                return False
        
        if p[-1] == s[-1] or p[-1] == '.':
            return self.isMatch(s[:-1], p[:-1])
        if p[-1] == '*':
            if p[-2] == s[-1] or p[-2] == '.':
                return self.isMatch(s[:-1], p[:-2]) or self.isMatch(s[:-1], p) or self.isMatch(s, p[:-2])
            else:
                return self.isMatch(s, p[:-2])
        return False
        # 1292 ms	13 MB  

• 动态规划法

边界条件：

1. s 和 p 均为空：True
2. p 空 s 不为空：False
3. s 空 p 最后一个字符是 *： $f(s,p[j-2])$
4. s 空 p 最后一个字符不是 *：False

动态方程：

1. p[j] == s[i]:m[i][j] = m[i-1][j-1]
2. p[j] == “.”: m[i][j] = m[i-1][j-1]
3. p[j] =="*":
   3.1. p[i-1] == s[i] or p[i-1] == “.”:
   dp[i][j] = dp[i-1][j] // 多个a的情况
   or dp[i][j] = dp[i][j-1] // 单个a的情况
   or dp[i][j] = dp[i][j-2] // 没有a的情况
   3.2. p[j-1] != s[i]:dp[i][j] = dp[i][j-2]

class Solution:
    def isMatch(self, s: str, p: str) -> bool:
        # 动态规划
        m = [[False for __ in range(len(p) + 1)] for _ in range(len(s) + 1)]
        m[0][0] = True
        for j in range(len(p)):
            if p[j] == '*':
                m[0][j + 1] = m[0][j - 1]
        
        for i in range(len(s)):
            for j in range(len(p)):
                if s[i] == p[j] or p[j] == '.':
                    m[i + 1][j + 1] = m[i][j]
                if p[j] == '*':
                    if p[j - 1] == s[i] or p[j - 1] == '.':
                        m[i + 1][j + 1] = m[i][j - 1] or m[i][j + 1] or m[i + 1][j - 1]
                    else:
                        m[i + 1][j + 1] = m[i + 1][j - 1]
        return m[len(s)][len(p)]
        # 	76 ms	13 MB   比递归法快接近20倍

 

55. 跳跃游戏

→_→

给定一个非负整数数组，你最初位于数组的第一个位置。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个位置。
示例 1:
输入: [2,3,1,1,4]
输出: true
解释: 从位置 0 到 1 跳 1 步, 然后跳 3 步到达最后一个位置。
示例 2:
输入: [3,2,1,0,4]
输出: false
解释: 无论怎样，你总会到达索引为 3 的位置。但该位置的最大跳跃长度是 0 ， 所以你永远不可能到达最后一个位置。

动态规划，贪心算法：自右向左，记录最左边一个“GOOD”（即可以跳到最后的位置）

class Solution:
    def canJump(self, nums):
        n = len(nums)
        leftmost_good = n - 1
        for i in range(n - 2, -1, -1):
            if nums[i] >= leftmost_good - i:
                leftmost_good = i
        return leftmost_good == 0

 

二、链表

141. 环形链表

→_→

给定一个链表，判断链表中是否有环。

快慢指针法：若有环，快指针跑一圈（或$n$圈）会追上慢指针，若无环，快指针最后指向l链表尾部或空。

class Solution(object):
    def hasCycle(self, head):
        fast = head
        slow = head
        while fast and fast.next:
            fast = fast.next.next
            slow = slow.next
            if fast == slow:
                return True
        return False

 

142. 环形链表 II

→_→

给定一个链表，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。
说明：不允许修改给定的链表。

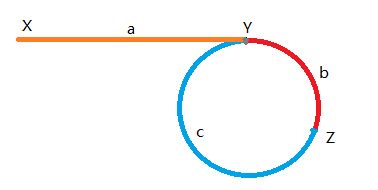
第一趟与141题一样，先用快慢指针判断是否有环，若有环，当快指针与慢指针在Z处相遇，慢指针走了 $a+b$ ，快指针走了 $a$ 然后绕了 $n$ 圈 $(n>=1)$ 后又走了 $b$ ，所以有 $2(a+b)=a+b+n(b+c)$ ，整理得 $a=c+(n-1)(b+c)$ ，于是令fast回到head，快慢指针以相同速度走，fast走了 $a$ 到Y，slow恰好走了 $c$ 加上 $n-1$ 圈回到Y处，此处即为入环的第一个节点。

class Solution(object):
    def detectCycle(self, head):
        if not head or not head.next:
            return 
        fast = head
        slow = head
        while fast and fast.next:
            fast = fast.next.next
            slow = slow.next
            if fast == slow:
                break
        if fast != slow:
            return 
        fast = head
        while fast != slow:
            fast = fast.next
            slow = slow.next
        return slow

 

148. 排序链表

→_→

在 O(n log n) 时间复杂度和常数级空间复杂度下，对链表进行排序。

归并排序

class Solution:
    def sortList(self, head: ListNode) -> ListNode:
        if not head or not head.next:
            return head
        fast = slow = temp = head
        while fast and fast.next:
            fast = fast.next.next
            temp = slow
            slow = slow.next
        temp.next = None
        
        h1 = self.sortList(head)
        h2 = self.sortList(slow)
        
        head = ListNode(0)
        p = head
        while h1 and h2:
            if h1.val > h2.val:
                p.next = h2
                h2 = h2.next
            else:
                p.next = h1
                h1 = h1.next
            p = p.next
        p.next = h1 if h1 else h2
        return head.next

 

23. 合并K个排序链表

→_→

合并 k 个排序链表，返回合并后的排序链表。请分析和描述算法的复杂度。

示例:
输入:
[
1->4->5,
1->3->4,
2->6
]
输出: 1->1->2->3->4->4->5->6

• 分治法：

class Solution:
    def mergeTwoLists(self, l1: ListNode, l2: ListNode) -> ListNode:
        ret = ListNode(0)
        p = ret
        while l1 and l2:
            if l1.val < l2.val:
                p.next = l1
                l1 = l1.next
            else:
                p.next = l2
                l2 = l2.next
            p = p.next
        if not l1:
            p.next = l2
        else:
            p.next = l1
        return ret.next
    
    def mergeKLists(self, lists: List[ListNode]) -> ListNode:
        ls = len(lists)
        if ls == 0:
            return
        if ls == 1:
            return lists[0]
        if ls == 2:
            return self.mergeTwoLists(lists[0], lists[1])
        return self.mergeTwoLists(self.mergeKLists(lists[:ls//2]), self.mergeKLists(lists[ls//2:]))

• 小顶堆优先队列：

def mergeKLists(self, lists: List[ListNode]) -> ListNode:
        for i in range(len(lists) - 1, -1, -1):
            if not lists[i]:
                lists.pop(i)
        if not lists:
            return
        
        # 构建最小堆
        ls = len(lists)
        for i in range(ls // 2 - 1, -1, -1):
            k = i
            v = lists[k]
            heap = False
            while not heap and 2 * k + 1 < ls:
                child = 2 * k + 1  # 左孩子
                if child < ls - 1 and lists[child].val > lists[child + 1].val:  # 两个孩子且右孩子小于左孩子
                    child += 1
                if v.val <= lists[child].val:
                    heap = True
                else:
                    lists[k] = lists[child]
                    k = child
            lists[k] = v
        
        ret = ListNode(0)
        p = ret
        while ls > 1:
            p.next = lists[0]
            p = p.next
            
            if lists[0].next:
                lists[0] = lists[0].next
            else:
                lists[0] = lists[-1]
                lists.pop()
                ls -= 1
            
            # 调整堆
            k = 0
            v = lists[0]
            heap = False
            while not heap and 2 * k + 1 < ls:
                child = 2 * k + 1
                if child < ls - 1 and lists[child].val > lists[child + 1].val:
                    child += 1
                if v.val <= lists[child].val:
                    heap = True
                else:
                    lists[k] = lists[child]
                    k = child
            lists[k] = v
            
        p.next = lists[0]
        return ret.next

时间复杂度：假设有$K$个链表，每个链表长度为$N$

• 暴力法： $O(N{K}^2)$ , 每找到一个最小值都要查找比较$K-1$次，总次数为$K\ast N\ast (K-1)$；
• 分治法： $O(KN{\log }_{2}K)$ , 最坏情况下，每$2$个表合并的时候需要查找比较2倍链表长度$2\ast N$次，也就是得到一个数需要比较$1$次，每一层合并需要$K\ast N$次，共需要合并$lo{g}_2(K)$层，总次数为$K\ast N\ast lo{g}_2(K)$；
• 堆： $O(KN\log_2 K) $
   

206. 反转链表

→_→

反转一个单链表。

迭代法标准写法

class Solution:
    def reverseList(self, head: ListNode) -> ListNode:
        cur = head
        pre = None
        while cur:
            nex = cur.next
            cur.next = pre
            pre = cur
            cur = nex
        return pre

递归法

class Solution:
    def reverseList(self, head: ListNode) -> ListNode:
        return self.recursive(head)[0]
    
    def recursive(self, head):
        if not head or not head.next:
            return head, head
        head_new, last = self.recursive(head.next)
        last.next = head
        head.next = None
        return head_new, head

 

三、二叉树

124. 二叉树中的最大路径和（困难）

→_→

给定一个非空二叉树，返回其最大路径和。
本题中，路径被定义为一条从树中任意节点出发，达到任意节点的序列。该路径至少包含一个节点，且不一定经过根节点。

示例 1:
输入: [1,2,3]

       1
      / \
     2   3
     
输出: 6

示例 2:
输入: [-10,9,20,null,null,15,7]

   -10
   / \
  9  20
    /  \
   15   7

输出: 42

对于任一非空节点，若最大路径包含它，那有两种情况：1.左右子树的最大路径值较大的那个加上该节点的值向上回溯； 2. 左右子树都在最大路径中, 加上该节点的值构成了最终的最大路径。因此更新最大值res的时候用r.val + left + right ，但向上回溯的时候只能选择其中一支，即return max(left, right)+ r.val。

这道题的遍历顺序应该是左右根自下向上的记录最大路径和，
返回包含此节点和此节点的一个叉的最大值。
      1
    /  \
   2    3
  / \  / \  
 4  5  6  7
 实际上是遍历所有根节点的路径，记录最大的值 
 例如： 根节点2： 4 5 2 
       根节点3： 6 7 3
       根节点1： 2 5 7 3 1 （这时左右子树不可能全要，只能要一个叉，左边是2-5， 右边是3-7）

class Solution:
    def maxPathSum(self, root: TreeNode) -> int:
        def max_path_sum(r):
            if not r:
                return 0
            left = max(0, max_path_sum(r.left))
            right = max(0, max_path_sum(r.right))
            self.res = max(self.res, r.val + left + right)
            return max(left, right) + r.val
        
        self.res = root.val
        max_path_sum(root)
        return self.res

 

230. 二叉搜索树中第K小的元素

→_→

给定一个二叉搜索树，编写一个函数 kthSmallest 来查找其中第 k 个最小的元素。
说明：
你可以假设 k 总是有效的，1 ≤ k ≤ 二叉搜索树元素个数。

示例 1:
输入: root = [3,1,4,null,2], k = 1
   3
  / \
 1   4
  \
   2
输出: 1

中序遍历

class Solution:
    def kthSmallest(self, root: TreeNode, k: int) -> int:
        self.k = k
        self.in_order(root)
        return self.res
        
    def in_order(self, root):
        if not root:
            return
        self.in_order(root.left)
        if self.k == 1:
            self.res = root.val
        if self.k == 0:
            return
        self.k -= 1
        self.in_order(root.right)

 

235. 二叉搜索树的最近公共祖先

→_→

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

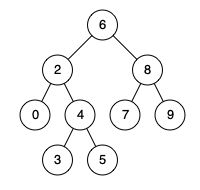
例如，给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]

示例 :
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6
解释: 节点 2 和节点 8 的最近公共祖先是 6。

两个节点都在当前根节点左侧，则递归左子树
两个节点都在当前根节点右侧，则递归右子树
否则返回该节点

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
        # 递归
        if not root:
            return
        v = root.val
        if v > p.val and v > q.val:
            return self.lowestCommonAncestor(root.left, p, q)
        elif v < p.val and v < q.val:
            return self.lowestCommonAncestor(root.right, p, q)
        return root

 

236. 二叉树的最近公共祖先

→_→

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

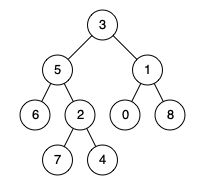
例如，给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]

示例 :
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出: 3
解释: 节点 5 和节点 1 的最近公共祖先是节点 3。

p，q必然存在树内, 且所有节点的值唯一
递归思想, 对以root为根的(子)树进行查找p和q, 如果root == null || p || q 直接返回root
表示对于当前树的查找已经完毕, 否则对左右子树进行查找, 根据左右子树的返回值判断：

1. 左右子树的返回值都不为null, 由于值唯一左右子树的返回值就是p和q, 此时root为LCA
2. 左右子树返回值均为null, p和q均不在子树中, 返回null
3. 如果左右子树返回值只有一个不为null, 说明只有p和q存在于左或右子树中, 最先找到的那个节点为LCA

class Solution:
    def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
        if not root or root == p or root == q:
            return root
        left = self.lowestCommonAncestor(root.left, p, q)
        right = self.lowestCommonAncestor(root.right, p, q)
        if left and right:
            return root
        if not left and not right:
            return None
        return left if left else right

 

四、位运算

136. 只出现一次的数字

→_→

给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。
说明：
你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗？

异或位运算：

• 交换律：a ^ b ^ c $\iff$ a ^ c ^ b
• 任何数于0异或为任何数 0 ^ n $\Rightarrow$ n
• 相同的数异或为0: n ^ n $\Leftarrow$ 0

var a = [2,3,2,4,4]
2 ^ 3 ^ 2 ^ 4 ^ 4 等价于 2 ^ 2 ^ 4 ^ 4 ^ 3 => 0 ^ 0 ^ 3 => 3

class Solution:
    def singleNumber(self, nums: List[int]) -> int:
        res = 0
        for a in nums:
            res ^= a
        return res

 

---

五、回溯法

46. 全排列

→_→

给定一个没有重复数字的序列，返回其所有可能的全排列。
示例:
输入: [1,2,3]
输出:
[
[1,2,3],
[1,3,2],
[2,1,3],
[2,3,1],
[3,1,2],
[3,2,1]
]

回溯法

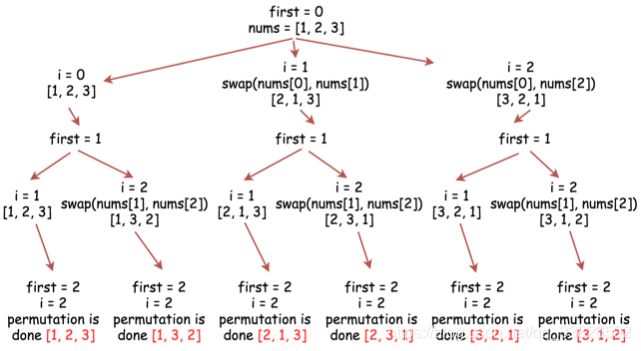
class Solution:
    def permute(self, nums):
        def backtrack(first):
            if first == n:
                res.append(nums[:])
            else:
                for i in range(first, n):
                    nums[first], nums[i] = nums[i], nums[first]
                    backtrack(first + 1)
                    nums[first], nums[i] = nums[i], nums[first]
    
        n = len(nums)
        res = []
        backtrack(0)
        return res

 

---

六、并查集

547. 朋友圈

→_→

班上有 N 名学生。其中有些人是朋友，有些则不是。他们的友谊具有是传递性。如果已知 A 是 B 的朋友，B 是 C 的朋友，那么我们可以认为 A 也是 C 的朋友。所谓的朋友圈，是指所有朋友的集合。
给定一个 N * N 的矩阵 M，表示班级中学生之间的朋友关系。如果M[i][j] = 1，表示已知第 i 个和 j 个学生互为朋友关系，否则为不知道。你必须输出所有学生中的已知的朋友圈总数。
示例 1:
输入:
[[1,1,0],
[1,1,0],
[0,0,1]]
输出: 2
说明：已知学生0和学生1互为朋友，他们在一个朋友圈。
第2个学生自己在一个朋友圈。所以返回2。

class Solution:
    def findCircleNum(self, M):
        class UnionFind:
            def __init__(self, n):
                self.count = n
                self.parent = [_ for _ in range(n)]

            def find(self, p):
                while p != self.parent[p]:
                    p = self.parent[p]
                return p

            def union(self, p, q):
                p_root = self.find(p)
                q_root = self.find(q)
                if p_root == q_root:
                    return
                self.parent[p_root] = q_root
                self.count -= 1
                
        m = len(M)
        union_find_set = UnionFind(m)
        for i in range(m):
            for j in range(i):
                if M[i][j] == 1:
                    union_find_set.union(j, i)

        return union_find_set.count

 

---

七、其它问题

15. 三数之和

→_→

给定一个包含 n 个整数的数组 nums，判断 nums 中是否存在三个元素 a，b，c ，使得 a + b + c = 0 ？找出所有满足条件且不重复的三元组。
注意：答案中不可以包含重复的三元组。

例如, 给定数组 nums = [-1, 0, 1, 2, -1, -4]，
满足要求的三元组集合为：
[
  [-1, 0, 1],
  [-1, -1, 2]
]

注意算法的复杂度（超时）和如何去重。步骤如下：

1. 数组排序；
2. 要找到 a,b,c 使得 a+b+c=0，只需对数组中的每个元素a（遍历），判断a之后的元素中是否存在b,c使得 b+c=-a，可用双指针法；
3. 去重，利用了数组的有序性，相同的两个数在数组中一定是相邻的，因此只需在遍历a时和移动指针时跳过相同的数，那么就不会有重复的三元组了。

class Solution:
    def threeSum(self, nums: List[int]) -> List[List[int]]:
        nums.sort()
        ret = []
        for i, a in enumerate(nums):
            if i and nums[i] == nums[i - 1]:
                continue
            left = i + 1
            right = len(nums) - 1
            while left < right:
                if nums[left] + nums[right] == -a:
                    ret.append([a, nums[left], nums[right]])
                    left += 1
                    right -= 1
                    while left < right and nums[left] == nums[left - 1]:
                        left += 1
                    while left < right and nums[right] == nums[right + 1]:
                        right -= 1
                elif nums[left] + nums[right] < -a:
                    left += 1
                else:
                    right -= 1
        return ret

16. 最接近的三数之和

→_→

给定一个包括 n 个整数的数组 nums 和 一个目标值 target。找出 nums 中的三个整数，使得它们的和与 target 最接近。返回这三个数的和。假定每组输入只存在唯一答案。
例如，给定数组 nums = [-1，2，1，-4], 和 target = 1.
与 target 最接近的三个数的和为 2. (-1 + 2 + 1 = 2).

与15题类似，排序 $\to$ 遍历 $\to$ 在内部使用双指针.

class Solution:
    def threeSumClosest(self, nums: List[int], target: int) -> int:
        nums.sort()
        ret = sum(nums[:3])
        for i in range(len(nums)):
            l = i + 1
            r = len(nums) - 1
            while l < r:
                s = nums[i] + nums[l] + nums[r]
                if s == target:
                    return s
                if abs(s - target) < abs(ret - target):
                    ret = s
                if s < target:
                    l += 1
                else:
                    r -= 1
        return ret

 

54. 螺旋矩阵

→_→

给定一个包含 m x n 个元素的矩阵（m 行, n 列），请按照顺时针螺旋顺序，返回矩阵中的所有元素。

示例 :
输入:
[
[ 1, 2, 3 ],
[ 4, 5, 6 ],
[ 7, 8, 9 ]
]
输出: [1,2,3,6,9,8,7,4,5]

取首行、取尾列，再翻转矩阵

class Solution:
    def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
        res = []
        while len(matrix) and len(matrix[0]):
            res.extend(matrix.pop(0))  # 取首行
            res.extend([line.pop() for line in matrix])  # 取尾列
            # 翻转180度
            matrix.reverse() 
            for line in matrix:
                line.reverse()
        return res

 

59. 螺旋矩阵 II

→_→

给定一个正整数 n，生成一个包含 1 到 n2 所有元素，且元素按顺时针顺序螺旋排列的正方形矩阵。

示例:
输入: 3
输出:
[
[ 1, 2, 3 ],
[ 8, 9, 4 ],
[ 7, 6, 5 ]
]

与54题步骤相反

class Solution:
    def generateMatrix(self, n: int) -> List[List[int]]:
        if n < 1:
            return
        nums = [i + 1 for i in range(n ** 2)]
        matrix = [[nums.pop()]]
        while nums:
            for line in matrix:
                line.reverse()
                line.append(nums.pop())
            matrix.append(nums[len(nums) - len(matrix[0]):])
            nums = nums[:len(nums) - len(matrix[0])]
            matrix.reverse()
        return matrix

 

238. 除自身以外数组的乘积

→_→

给定长度为 n 的整数数组 nums，其中 n > 1，返回输出数组 output ，其中 output[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积。

示例:
输入: [1,2,3,4]
输出: [24,12,8,6]
说明: 请不要使用除法，且在 O(n) 时间复杂度内完成此题。
进阶：你可以在常数空间复杂度内完成这个题目吗？（ 出于对空间复杂度分析的目的，输出数组不被视为额外空间。）

分别向左向右跑两趟，得到两个数组left,right，每个元素分别表示其左边/右边的所有数乘积，然后两个数组对应元素相乘即可
进阶：先向左跑一遍，然后在同一个数组向右再跑一遍，以达到常数空间复杂度

class Solution:
    def productExceptSelf(self, nums: List[int]) -> List[int]:
        # 进阶  常数空间复杂度
        if not nums:
            return nums
        n = len(nums)
        res = [1] * n
        for i in range(1, len(nums)):
            res[i] = res[i - 1] * nums[i - 1]
        right = nums[-1]
        for i in range(len(nums) - 2, -1, -1):
            res[i] *= right
            right *= nums[i]
        return res

# class Solution:
#     def productExceptSelf(self, nums: List[int]) -> List[int]:
#         if not nums:
#             return nums
#         n = len(nums)
#         left = [1] * n
#         right = [1] * n
#         for i in range(1, n):
#             left[i] = left[i - 1] * nums[i - 1]
#             right[n - i - 1] = right[n - i] * nums[n - i]
#         for i in range(n):
#             right[i] *= left[i]
#         return right