Algorithm Analysis: common functions, asymptotic notation
对于算法复杂度分析很多概念,自己理解的稀里糊涂的。或者好不容易弄明白了,隔一段时间又忘记了。特地整理记录在此
1. common functions used in analysis
constant, logarithmic, linear, N-log-N, quadratic, cubic, exponential
From best (least resource requirements ) to worst, the rankings are: O(1), O(logn), O(n), O(nlogn), O( n^2 ), O(n^3)O(2^n).
Graph: https://en.wikipedia.org/wiki/Analysis_of_algorithms
2. asymptotic notations
Big O, Little o, Theta, Omega, Little w
3. involved math knowledge
3.1 exponent
8^2 could be called "8 to the power 2" or "8 to the second power", or simply "8 squared"
5^3 could be called "5 to the third power", "5 to the power 3" or simply "5 cubed"
2^4 could be called "2 to the fourth power" or "2 to the power 4" or simply "2 to the 4th"
a^n tells you to multiply n times a by itself, so there are n of those a'
3.2 laws of exponent
3.3 logarithm
A Logarithm says how many of one number to multiply to get another number. Example, what is x in log3(x) = 5
Start with:log3(x) = 5. We want to "undo" the log3 so we can get "x ="
Use the Exponential Function (on both sides):![]()
And we know that ![]() , so:x = 35
, so:x = 35
Answer:x = 243
3.4 Series
3.4.1 等差数列 Arithmetic Series
To sum up the terms of this arithmetic sequence:
a + (a+d) + (a+2d) + (a+3d) + ...
use this formula:
3.4.2 等比数列 Geometric Series
a + ar + ar^2 + ... + ar^(n-1)
Each term is ar^k, where k starts at 0 and goes up to n-1
Use this formula:
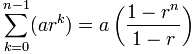
a is the first term
r is the "common ratio" between terms
n is the number of terms
4. Reference
Algebra
Calculus
