数学建模中的插值算法

一、介绍
数模比赛中，常常需要根据已知的函数点进行数据、模型的处理和分析，而有时候现有的数据是极少的，不足以支撑分析的进行，这时就需要使用一些数学的方法，“模拟产生”一些新的但又比较靠谱的值来满足需求，这就是插值的作用。

经常使用的插值算法有四种
1、拉格朗日插值
2、牛顿插值
3、分段三次Hermite插值
4、样条插值

二、具体介绍五种插值算法
1、拉格朗日插值和牛顿插值

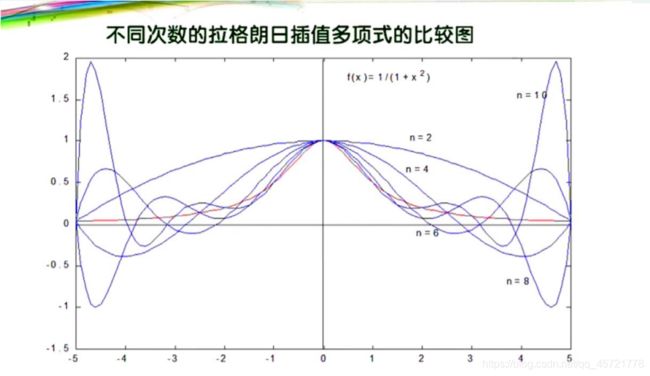
在使用这两种方法的时候，我们发现，在插值次数比较少的时候函数曲线还是和目标函数的图像比较接近，不过在高次插值的时候，即在横坐标为4.5左右的时候，会出现龙格现象。所以在不熟悉运动曲线趋势的时候我们不要轻易使用这两种方法，以免发生错误。

龙格现象：即在两端处波动极大,产生明显的震荡。

下面我们主要介绍以下两种方法

2、分段三次埃米尔特(Hermite)插值

埃尔米特插值多项式就是不但要求在节点上的函数值相等，而且还要求对应的导数值也相等,甚至要求高阶导数也相等，满足这种要求的插值多项式.。

直接使用Hermite插值得到的多项式次数较高，也存在着龙格现象，因此在实际应用中，往往使用分段三次Hermite插值多项(PCHIP)。

Matlab有内置的函数（实现过程已经帮我们封装好了，会调用就行了)∶

p = pchip(x,y, new_x)

x是已知的样本点的横坐标;y是已知的样本点的纵坐标;new_x是要插入处对应的横坐标

代码为

% 分段三次埃尔米特插值
x = -pi:pi; y = sin(x); 
new_x = -pi:0.1:pi;
p = pchip(x,y,new_x);
figure(1); 
plot(x, y, 'o', new_x, p, 'r-')

3、三次样条插值

Matlab有内置的函数:

p = spline(x,y, new_x)

x是已知的样本点的横坐标;y是已知的样本点的纵坐标;new_x是要插入处对应的横坐标

x = ‐pi:pi;
y = sin(x);
new_x = ‐pi:0.1:pi;
p2 = spline(x,y,new_x); %三次样条插值
plot(x,y,'o',new_x,p1,'r‐',new_x,p2,'b‐')
legend('样本点','三次埃尔米特插值','三次样条插值',‘Location’,‘SouthEast’) %标注显示在东南方向

下面是分段三次埃米尔特插值和三次样条插值的对比

% 三次样条插值和分段三次埃尔米特插值的对比
x = -pi:pi; 
y = sin(x); 
new_x = -pi:0.1:pi;
p1 = pchip(x,y,new_x);   %分段三次埃尔米特插值
p2 = spline(x,y,new_x);  %三次样条插值
figure(2);
plot(x,y,'o',new_x,p1,'r-',new_x,p2,'b-')
legend('样本点','三次埃尔米特插值','三次样条插值','Location','SouthEast')   %标注显示在东南方向

我们可以发现，三次样条插值的精确度比三次埃米特插值的精确度还要高

参考文章：清风老师