编译原理-(NFA->DFA)

网上的一堆人，你们是猪么？
找了一大堆东西都TM说不到点上。
直接开讲。

为什么NFA->DFA

nfa有回溯，回溯太TM浪费资源。

怎么判断是NFA还是DFA

都是图吧。
给我找度。
一个节点的出度给我仔细的看。
如果出度有1个，那么这个节点OK.确定了。
如果出度有2个，再看是不是1个出去回到自己，然后1个出去指向别人。这样的话也OK。
但你不能2个一个出去指向B，另一个出去指向C。

NFA怎么到DFA

给我拿到NFA。
先给我画个图。

|  集合  |  Ia  |  Ib |
|       |      |      | 
|       |      |      | 
|       |      |      | 
...

这个图的Ia,Ib,代表吃a，吃b.

下一步给我确定开始集合。
首先把NFA的开始节点给我写到集合下面的第一行。
这个时候求这个节点的epsilon 闭包。

怎么求epsilon闭包。

看我添加闭包的顺序

0的epsilon闭包:{0,1,2,4,7}
1的epsilon闭包:{1,2,4}
2的epsilon闭包:{2}
3的epsilon闭包:{3,6,1,2,4,7}
4的epsilon闭包:{4}
5的epsilon闭包:{5,6,1,2,4,7}
6的epsilon闭包:{6,1,2,4,7}
7的epsilon闭包:{7}
8的epsilon闭包:{8}
9的epsilon闭包:{9}
OK?

---

接上文

NFA怎么到DFA

给我拿到NFA。
先给我画个图。

|  集合  |  Ia  |  Ib |
|       |      |      | 
|       |      |      | 
|       |      |      | 
...

这个图的Ia,Ib,代表吃a，吃b.

下一步给我确定开始集合。
首先把NFA的开始节点给我写到集合下面的第一行。
这个时候求这个节点的epsilon 闭包。
开始节点就是所求的这个节点的epsilon 闭包。
注意:Ia下面的怎么填?

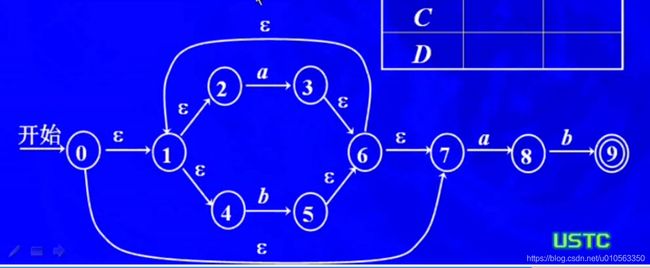
0的epsilon闭包:{0,1,2,4,7}
那就找，找0的epsilon闭包的所有节点看谁吃了a。

0没有，1没有。2吃了,到3.，把3填到这个表格，并且做个标记。
4没有，7吃了，到8.同理，把8填。

集合	I0	I1
{0,1,2,4,7}	{ 3,8,}

这个时候，做3,8的epsilon闭包。
3的epsilon闭包:{3,6,1,2,4,7}
8的epsilon闭包:{8}
然后，将他们合并，添加到Ia下面第一行。

集合	I0	I1
{0,1,2,4,7}	{ 3,8,6,1,2,4,7}

并且恢复顺序。最好是填的时候就恢复顺序。

集合	I0	I1
{0,1,2,4,7}	{1,2,3,4,6,7,8}

这样I0就填好了。
下面就是不断的填I0,I1。
如果I0,I1下面出现新的集合，例如B:

集合	I0	I1
A	B

上面的是下面的简化版:

集合	I0	I1
{0,1,2,4,7}	{1,2,3,4,6,7,8}

---

那么，将B填到集合第2行:例如:

集合	I0	I1
A	B
B

如果I0,I1下面推不出来，那么你就不填。我的做法是写个空,表示空集.

这样按照A,B,C,D,…的顺序填写。
知道再也生成不了新的符号，且所有的符号都出现在集合那一列下面。
OK。

怎么确定结束集合?

寻找NFA中为结束的状态，在DFA中的集合下面找，找到那个集合包含NFA中的结束状态，那么这个集合就是结束集合。

集合	Ia	Ib
A	空	B
B	C	D
C	C	D
D	空	空

假如D里面有状态5,5在NFA中是一个结束状态，那么D就是DFA的结束状态。
OK。