使用2D卷积技术进行时间序列预测
本文将展示一种新的时间序列预测方法。
目标数据集
在这个项目中使用的数据是来自北卡罗来纳州夏洛特分校的全球能源预测竞赛的数据。您可以在这里找到更多信息:http://www.drhongtao.com/gefcom/2017
你需要知道的是,这些数据是来自能源网络的各种读数。我们的目标是利用这些数据点预测电网的实时能源需求。数据点还包括露点和干球温度,因为空调是能源消耗的主力。
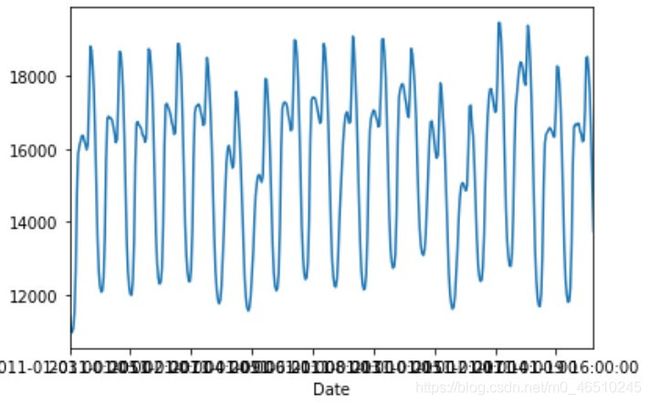
我们的目标变量是RTDemand(Real Time energy demand):电网的实时能源需求。数据具有清晰的日周期特征。以下是我们三天的数据:
在每个人都在睡觉的半夜里,我们的耗电量达到最低。我们早上醒来,开始工作,当太阳达到峰值强度时,我们的能量消耗达到了最大值。因此可以认为每天的能耗下降与通勤时间相对应。
如果我们再把尺度放大一些,我们可以看到清晰的自相关特性和日趋势。以下是大约3周的数据:
三周内的每小时数据
我们还可以注意到一个更大的季节性趋势,如果我们进一步缩小并查看一整年的数据:
一年内的每小时数据
由此看见,这是一个相当理想的时间序列数据,可以对其进行预测。
单变量纯时间序列预测模型
对于时间序列预测,我们将需要给定一个目标结果的时间序列。在我们的例子中,我选择72小时作为时间序列的长度。这意味着我们模型的输入是72个单独的数字,代表过去72小时的数据,我们希望从模型中得到的目标输出是它对第73小时的预测。我认为72小时是一个很好的长度,因为它可以很好地捕捉当地的趋势和昼夜循环。
以下是我们对模型的输入(连续三天的数据):
array([
[12055., 11430., 10966., 10725., 10672., 10852., 11255., 11583.,
12238., 12877., 13349., 13510., 13492., 13314., 13156., 13364.,
14632., 15653., 15504., 15088., 14579., 13882., 12931., 11883.,
10978., 10406., 10089., 9982., 10031., 10289., 10818., 11444.,
12346., 13274., 13816., 14103., 14228., 14154., 14055., 14197.,
15453., 16531., 16410., 15954., 15337., 14347., 13178., 12106.,
11400., 11059., 10959., 11073., 11485., 12645., 14725., 15863.,
16076., 16222., 16358., 16362., 16229., 16123., 15976., 16127.,
17359., 18818., 18724., 18269., 17559., 16383., 14881., 13520.],
[11430., 10966., 10725., 10672., 10852., 11255., 11583., 12238.,
12877., 13349., 13510., 13492., 13314., 13156., 13364., 14632.,
15653., 15504., 15088., 14579., 13882., 12931., 11883., 10978.,
10406., 10089., 9982., 10031., 10289., 10818., 11444., 12346.,
13274., 13816., 14103., 14228., 14154., 14055., 14197., 15453.,
16531., 16410., 15954., 15337., 14347., 13178., 12106., 11400.,
11059., 10959., 11073., 11485., 12645., 14725., 15863., 16076.,
16222., 16358., 16362., 16229., 16123., 15976., 16127., 17359.,
18818., 18724., 18269., 17559., 16383., 14881., 13520., 12630.],
[10966., 10725., 10672., 10852., 11255., 11583., 12238., 12877.,
13349., 13510., 13492., 13314., 13156., 13364., 14632., 15653.,
15504., 15088., 14579., 13882., 12931., 11883., 10978., 10406.,
10089., 9982., 10031., 10289., 10818., 11444., 12346., 13274.,
13816., 14103., 14228., 14154., 14055., 14197., 15453., 16531.,
16410., 15954., 15337., 14347., 13178., 12106., 11400., 11059.,
10959., 11073., 11485., 12645., 14725., 15863., 16076., 16222.,
16358., 16362., 16229., 16123., 15976., 16127., 17359., 18818.,
18724., 18269., 17559., 16383., 14881., 13520., 12630., 12223.]
])
输入数组中的每一个数字都是RTDemand的读数:这个特定的发电站每小时需要多少千瓦的电力。每个数组中都有72个小时的数据。如果你仔细观察这3个数组中前8个左右的读数,你会注意到每一个新的数组都是一个向前移动了1小时的序列。因此,这72个长度的输入数组中的每一个数据都代表了最后72小时对这个能源网实时需求的读数。
我们需要预测第73小时的需求,所以目标数组格式如下:
array([[12630.],
[12223.],
[12070.]])
需要注意的是,目标数组中的第一个数据是输入数组中第二个数组的最后一个数据,目标数组中的第二个数据是输入数组中第三个数组的最后一个数据。也就是说,我们通过输入数组中的第一个数组来实现对于目标数组中第一个数据的预测。
数据转换
一旦我们加载了数据,接下来我们需要将其转换成一个适当的数据集,用于训练机器学习模型。首先,缩放所有输入变量。稍后,我们将讨论如何使用数据集的所有12个输入,但现在将只使用1个变量作为输入,以便于介绍本文使用的预测方法。本文不会对目标变量Y进行缩放处理,因为它可以使监控模型的进度变得更容易,成本最低。接下来,我们将把数据分为一个训练集和一个测试集:
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X = scaler.fit_transform(X)
split = int(0.8 * len(X))
X_train = X[: split - 1]
X_test = X[split:]
y_train = y[: split - 1]
y_test = y[split:]
最后,我们将使用的模型的输入是(Samples、Timesteps、Features)。在第一个模型中,我们只使用时间窗口的目标变量作为输入。所以,我们只有一个输入特征Feature。我们的输入即为(Samples,Timesteps)。在进行训练集和测试集分割之后,我们现在将对其进行reshape处理:
X_train = X_train.reshape((X_train.shape[0], X_train.shape[1], 1))
X_test = X_test.reshape((X_test.shape[0], X_test.shape[1], 1))
X_train.shape
(61875, 72, 1)
也就是说,第一个模型的输入数据为61875个样本、每个样本包含有72小时数据以及1个特征。
基线模型
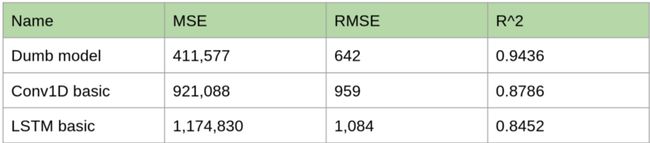
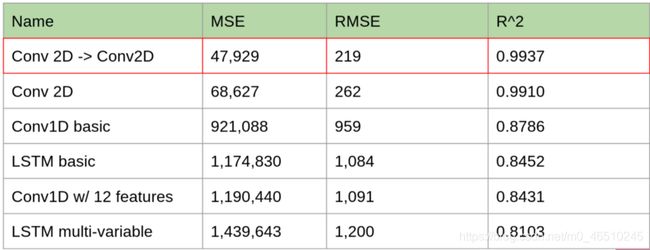
首先,我们建立一个基线模型。我们的优化函数设置为均方误差/均方根误差。我们同时也监测R²,不过,如果存在冲突,我们只使用均方误差作为损失函数和优化目标。
对于基线模型,我们将看到均方误差和R²的数据情况。这里的基准模型实现的功能是猜测时间序列中先前的值。下面是相关代码:
# Benchmark model
prev_val = y_test[0]
sse = 0
for n in range(0, len(y_test)-1):
err = y_test[n] — prev_val
sq_err = err ** 2
sse = sse + sq_err
prev_val = y_test[n]
mse = sse / n
mse
使用我们的测试数据集,得到的平方根误差是641.54。也就是说,这个基准模型在给定的一小时内会相对于真实情况相差641.54兆瓦。这是基准模型与实际结果的图表:
真实数据曲线&基准模型预测曲线
虽然第一个模型很简单,但是性能上表现出的效果良好。接下来我们尝试其它的模型方法。
LSTM预测模型
时间序列数据预测常用的模型之一就是LSTM。相对于本文提出的卷积预测模型,它是一个很有意义的对照模型。LSTM预测的相关代码如下:
def basic_LSTM(window_size=5, n_features=1):
new_model = keras.Sequential()
new_model.add(tf.keras.layers.LSTM(100,
input_shape=(window_size, n_features),
return_sequences=True,
activation=’relu’))
new_model.add(tf.keras.layers.Flatten())
new_model.add(tf.keras.layers.Dense(1500, activation=’relu’))
new_model.add(tf.keras.layers.Dense(100, activation=’linear’))
new_model.add(tf.keras.layers.Dense(1))
new_model.compile(optimizer=”adam”, loss=”mean_squared_error”)
return new_model
ls_model = basic_LSTM(window_size=window_size, n_features=X_train.shape[2])
ls_model.summary()
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
lstm (LSTM) (None, 72, 100) 40800
_________________________________________________________________
flatten (Flatten) (None, 7200) 0
_________________________________________________________________
dense (Dense) (None, 1500) 10801500
_________________________________________________________________
dense_1 (Dense) (None, 100) 150100
_________________________________________________________________
dense_2 (Dense) (None, 1) 101
=================================================================
Total params: 10,992,501
Trainable params: 10,992,501
Non-trainable params: 0
通过训练数据集进行模型训练,然后通过测试集进行评价:
ls_model.evaluate(X_test, y_test, verbose=0)
1174830.0587427279
from sklearn.metrics import r2_score
predictions = ls_model.predict(X_test)
test_r2 = r2_score(y_test, predictions)
test_r2
0.8451637094740732
我们得到的结果不是很好。具体地说,我们最终得到的误差比之前的基准模型更高。下面的图表可以了解它的预测情况:

LSTM预测结果
正如上图所示,LSTM的预测具有较大的不确定性。
1D卷积预测方法
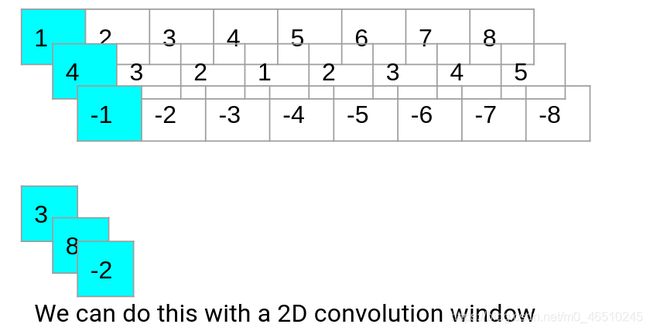
另一种预测时间序列的方法是使用一维卷积模型。1D卷积使用一个过滤窗口并在数据上循环该窗口以产生新的输出。根据所学的卷积窗参数,它们可以像移动平均线、方向指示器或模式探测器一样随时间变化。
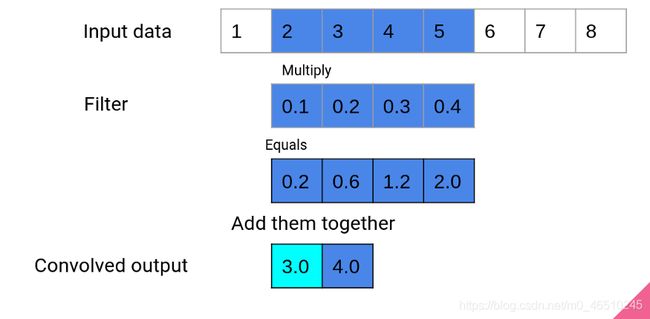
step 1
这里有一个包含8个元素的数据集,过滤器大小为4。过滤器中的四个数字是Conv1D层学习的参数。在第一步中,我们将过滤器的元素乘以输入数据,并将结果相加以产生卷积输出。
step 2
在卷积的第二步中,窗口向前移动一个,重复相同的过程以产生第二个输出。
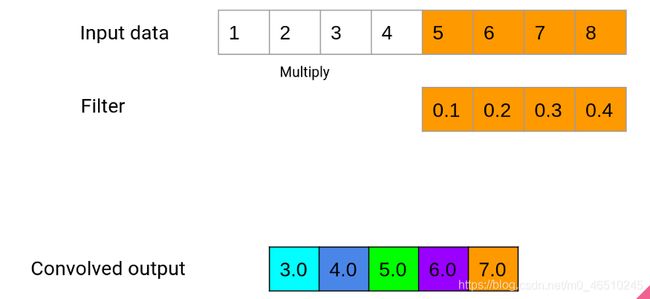
Last step
这个过程一直持续到窗口到达输入数据的末尾。在我们的例子中,一个输入数据序列是我们之前设置的72小时的数据。如果我们添加padding=“same”选项,我们的输入数据将在开始和结束处用零进行填充,以保持输出长度等于输入长度。上面的演示使用线性激活,这意味着最后一个多色数组是我们的输出。但是,我们可以在这里使用一整套激活函数,这些函数将通过一个额外的步骤来运行这个数字。因此,在下面的例子中,将有一个ReLU激活函数应用于最后的输出,以产生最终的输出。
下面展示了建立1D卷积模型的相关代码:
def basic_conv1D(n_filters=10, fsize=5, window_size=5, n_features=2):
new_model = keras.Sequential()
new_model.add(tf.keras.layers.Conv1D(n_filters, fsize, padding=”same”, activation=”relu”, input_shape=(window_size, n_features)))
# Flatten will take our convolution filters and lay them out end to end so our dense layer can predict based on the outcomes of each
new_model.add(tf.keras.layers.Flatten())
new_model.add(tf.keras.layers.Dense(1800, activation=’relu’))
new_model.add(tf.keras.layers.Dense(100))
new_model.add(tf.keras.layers.Dense(1))
new_model.compile(optimizer=”adam”, loss=”mean_squared_error”)
return new_model
模型情况如下:
univar_model = basic_conv1D(n_filters=24, fsize=8, window_size=window_size, n_features=X_train.shape[2])
univar_model.summary()
Model: "sequential_1"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
conv1d (Conv1D) (None, 72, 24) 216
_________________________________________________________________
flatten_1 (Flatten) (None, 1728) 0
_________________________________________________________________
dense_3 (Dense) (None, 1800) 3112200
_________________________________________________________________
dense_4 (Dense) (None, 100) 180100
_________________________________________________________________
dense_5 (Dense) (None, 1) 101
=================================================================
Total params: 3,292,617
Trainable params: 3,292,617
Non-trainable params: 0
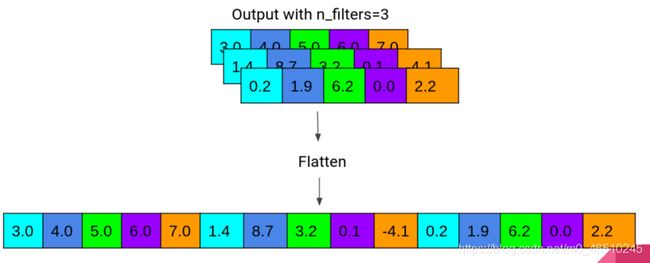
注意,这里有24个卷积窗口,过滤器大小是8。因此,在我们的例子中,输入数据将是72小时,这将创建一个大小为8的窗口,其中将有24个过滤器。因为我使用padding=“same”,每个过滤器的输出宽度将是72,就像我们的输入数据一样,并且输出的数量将是24个卷积数组。最后通过Flatten生成72*24=1728长度的数组。Flatten的工作过程如下图所示:
Flatten工作示意图
对比1D卷积模型、LSTM、基线模型的预测损失如下:
显然1D卷积方法比LSTM更好一些,但是它仍然没有达到最初的基准模型更好的效果。当我们看预测效果曲线时,我们可以看到这个模型有明显的偏差:
1D卷积预测效果
添加数据维度
在上面的例子中,我们只使用我们想要预测的特性作为我们的输入变量。然而,我们的数据集有12个可能的输入变量。我们可以将所有的输入变量叠加起来,然后一起使用它们来进行预测。由于许多输入变量与我们的输出变量具有中等/较强的相关性,因此使用更多的数据进行更好的预测应该是可能的。
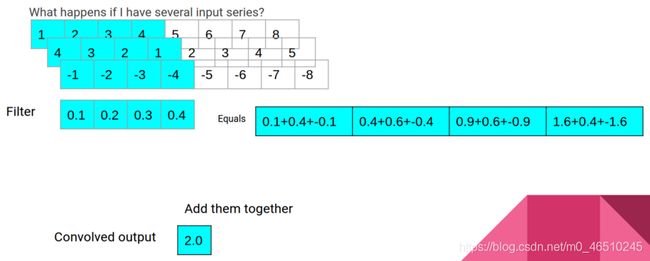
多输入1D卷积
如果我想把一个不同的数据序列叠加到模型中,首先要通过相同的窗口处理过程来生成一组观测值,每个观测值都包含变量的最后72个读数。例如,如果我想在第1列中添加变量DADemand(日前需求,当前前一天的需求),将对其执行以下操作:
(DADemand, _) = window_data(gc_df, window_size, 1, 1)
scaler = StandardScaler()
DADemand = scaler.fit_transform(DADemand)
split = int(0.8 * len(X))
DADemand_train = DADemand[: split — 1]
DADemand_test = DADemand[split:]
DADemand_test.shape
(61875, 72, 1)
然后,可以对所有的12个变量重复这个过程,并将它们堆积成一个单独的集合,如下所示:
data_train = np.concatenate((X_train, db_train, dew_train, DADemand_train, DALMP_train, DAEC_train, DACC_train, DAMLC_train, RTLMP_train, RTEC_train, RTCC_train, RTMLC_train), axis=2)
data_test = np.concatenate((X_test, db_test, dew_test, DADemand_test, DALMP_test, DAEC_test, DACC_test, DAMLC_test, RTLMP_test, RTEC_test, RTCC_test, RTMLC_test), axis=2)
data_train.shape
(61875, 72, 12)
至此生成了包含61875个样本、每一个都包含12个不同时间序列的72小时单独读数的数据集。我们现在通过一个Conv1D网络来运行它,看看我们得到了什么结果。如果回顾一下我们用于创建这些模型的函数,会注意到其中一个变量是特征feature的数量,因此运行这个新模型的代码同样十分简单。预测误差结果如下:
模型的性能实际上随着其他变量的增加而降低。分析其原因,可能是“模糊”效应(添加更多的数据集往往会“模糊”任何一个特定输入变化的影响,反而会产生一个不太精确的模型。)。
2D卷积
我们实际需要的是一个卷积窗口,它可以查看我们的模型特征并找出哪些特征是有益的。2D卷积可以实现我们想要的效果。
在做了一些尝试之后,本文将使用(1,filter_size)大小的2D卷积窗口,在上图中,filter_size=3。回到我们的能源预测问题,我们有12个特点。为了让它进入二维卷积窗口,我们实际上需要它有4个维度。我们可以通过以下方法得到另一个维度:
data_train_wide = data_train.reshape((data_train.shape[0], data_train.shape[1], data_train.shape[2], 1))
data_test_wide = data_test.reshape((data_test.shape[0], data_test.shape[1], data_test.shape[2], 1))
data_train_wide.shape
(61875, 72, 12, 1)
测试了不同的窗口尺寸过后,我们发现一次考虑两个特征效果最好:
def basic_conv2D(n_filters=10, fsize=5, window_size=5, n_features=2):
new_model = keras.Sequential()
new_model.add(tf.keras.layers.Conv2D(n_filters, (1,fsize), padding=”same”, activation=”relu”, input_shape=(window_size, n_features, 1)))
new_model.add(tf.keras.layers.Flatten())
new_model.add(tf.keras.layers.Dense(1000, activation=’relu’))
new_model.add(tf.keras.layers.Dense(100))
new_model.add(tf.keras.layers.Dense(1))
new_model.compile(optimizer=”adam”, loss=”mean_squared_error”)
return new_model
m2 = basic_conv2D(n_filters=24, fsize=2, window_size=window_size, n_features=data_train_wide.shape[2])
m2.summary()
Model: "sequential_4"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
conv2d (Conv2D) (None, 72, 12, 24) 72
_________________________________________________________________
flatten_4 (Flatten) (None, 20736) 0
_________________________________________________________________
dense_12 (Dense) (None, 1000) 20737000
_________________________________________________________________
dense_13 (Dense) (None, 100) 100100
_________________________________________________________________
dense_14 (Dense) (None, 1) 101
=================================================================
Total params: 20,837,273
Trainable params: 20,837,273
Non-trainable params: 0
这个模型相当大。在普通CPU上训练每一个epoch大约需要4分钟。不过,当它完成后,预测效果如下图:
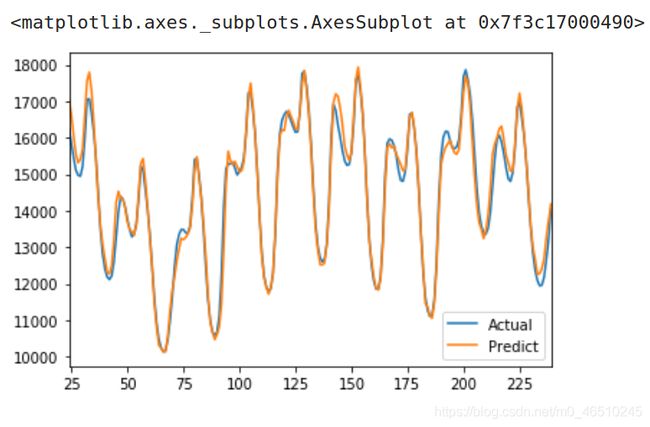
可以看到,2D卷积的效果优于其它所有的预测模型。
补充
如果我们使用类似的想法,但同时用尺寸为(8,1)的滤波器进行卷积运算呢?相关代码如下:
def deeper_conv2D(n_filters=10, fsize=5, window_size=5, n_features=2, hour_filter=8):
new_model = keras.Sequential()
new_model.add(tf.keras.layers.Conv2D(n_filters, (1,fsize), padding=”same”, activation=”linear”, input_shape=(window_size, n_features, 1)))
new_model.add(tf.keras.layers.Conv2D(n_filters, (hour_filter, 1), padding=”same”, activation=”relu”))
new_model.add(tf.keras.layers.Flatten())
new_model.add(tf.keras.layers.Dense(1000, activation=’relu’))
new_model.add(tf.keras.layers.Dense(100))
new_model.add(tf.keras.layers.Dense(1))
new_model.compile(optimizer=”adam”, loss=”mean_squared_error”)
return new_model
本文所有代码和数据可以在这里直接下载:
https://github.com/walesdata/2Dconv_pub
作者:Johnny Wales
deephub翻译组:oliver lee