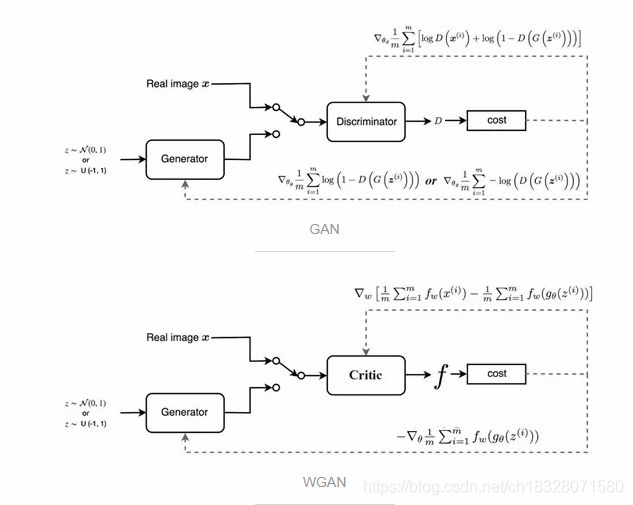
GAN的系列经典模型讲解

---

---

概述

自从Goodfellow2014年提出这个想法之后，生成对抗网络（GAN）就成了深度学习领域内最火的一个概念，包括LeCun在内的许多学者都认为，GAN的出现将会大大推进AI向无监督学习发展的进程。

于是，研究GAN就成了学术圈里的一股风潮，几乎每周，都有关于GAN的全新论文发表。而学者们不仅热衷于研究GAN，还热衷于给自己研究的GAN起名，比如什么3D-GAN、BEGAN、iGAN等;GAN千奇百怪、应有尽有，形成了GANs的动物园。

下边，就来讨论一些比较经典的GAN架构的文章。

一、CGAN

1、基本思想

在原始GAN网络中，与其他生成式模型相比，GAN这种竞争的方式不再要求一个假设的数据分布，即不需要formulate p(x)，而是使用一种分布直接进行采样sampling，从而真正达到理论上可以完全逼近真实数据，这也是GAN最大的优势。然而，这种不需要预先建模的方法缺点是太过自由了，对于较大的图片，较多的 pixel的情形，基于简单 GAN 的方式就不太可控了。为了解决GAN太过自由这个问题，一个很自然的想法是给GAN加一些约束，于是便有了Conditional Generative Adversarial Nets（CGAN）。

生成器和判别器都以某些额外信息y为条件，即把生成对抗网络扩展到条件模型。y可以是任何类型的辅助信息。CGAN可以通过将y作为附加输入，馈入判别器和生成器来执行调节。

2、模型简介

条件生成对抗网络（CGAN）是对原始GAN的一个扩展，生成器和判别器都增加额外信息 y为条件, y 可以使任意信息,例如类别信息,或者其他模态的数据。如 Figure 1 所示，通过将额外信息 y 输送给判别模型和生成模型,作为输入层的一部分,从而实现条件GAN。在生成模型中,先验输入噪声 $p(z)$ 和条件信息 $y$ 联合组成了联合隐层表征。对抗训练框架在隐层表征的组成方式方面相当地灵活。类似地，CGAN 的目标函数是带有条件概率的二人极小极大值博弈（two-player minimax game ）：

CGAN的网络结构：

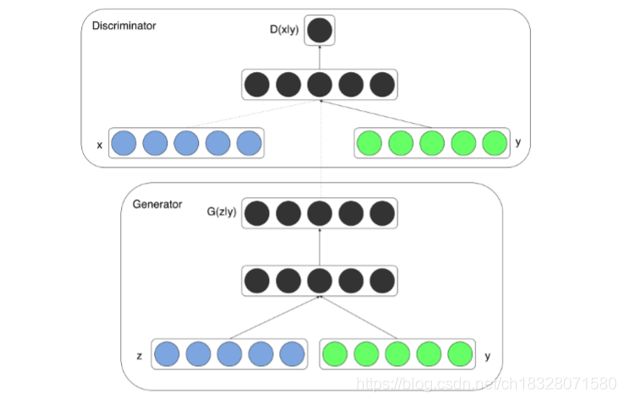
3、 应用

1、CGAN可以把类别标签当作条件，生成是具有该类别的图像。

在MNIST上以类别标签为条件（one-hot编码）训练条件GAN，可以根据标签条件信息，生成对应的数字。生成模型的输入是100维服从均匀分布的噪声向量，条件变量y是类别标签的one hot编码。噪声z和标签y分别映射到隐层(200和1000个单元),在映射到第二层前,联合所有单元。最终有一个sigmoid生成模型的输出(784维)，即28*28的单通道图像。

判别模型的输入是784维的图像数据和条件变量y（类别标签的one hot编码），输出是该样本来自训练集的概率。

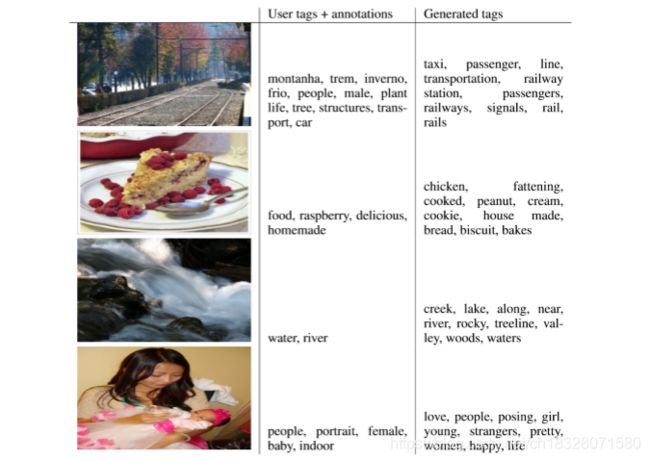
2、CGAN广泛用于多模态（图像、文本等为不同模态）学习的图像自动标注

下图为多模态的结果展示，第一列为图像，第二列为用户标注，将第一列第二列输入CGAN生成第三列的标签。

二、DCGAN

1、基本思想

这是第一次在GAN中使用卷积神经网络并取得了非常好的结果。之前，CNN在计算机视觉方面取得了前所未有的成果。但在GAN中还没有开始应用CNNs。Alec Radford，Luke Metz，Soumith Chintala等人“Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks”提出了DCGAN。这是GAN研究的一个重要里程碑，因为它提出了一个重要的架构变化来解决训练不稳定，模式崩溃和内部协变量转换等问题。从那时起，基于DCGAN的架构就被应用到了许多GAN架构。

近年来，使用卷积网络（CNN）的监督学习已经在计算机视觉应用中得到了广泛的应用。相比之下，CNN的无监督学习受到的关注较少。

动机：希望帮助弥合CNNs在监督学习和无监督学习之间的差距。提出了一类称为深度卷积生成对抗网络（DCGAN）深度卷积生成对抗网络（DCGAN），具有某些架构约束，并证明了他们是无监督学习的有利方法。

还将学习的特征作用于新任务——证明了作为一般图像表示的适用性。

2、模型简介

DCGAN是将CNN与GAN的一种结合。

其将卷积网络引入到生成式模型当中来做无监督的训练，利用卷积网络强大的特征提取能力来提高生成网络的学习效果。

DCGAN的原理和GAN对抗生成是一样的。它只是把GAN的G和D换成了两个卷积神经网络（CNN），但不是直接换就可以了。

DCGAN对卷积神经网络的结构做了一些改变，以提高样本的质量和收敛的速度，这些改变有：

• 取消所有pooling层。G网络中使用转置卷积（transposed convolutional
  layer）进行上采样，D网络中用加入stride的卷积代替pooling；

• 除了生成器模型的输出层和判别器模型的输入层，在网络其它层上都使用了BatchNormalization，使用BN可以稳定学习，有助于处理初始化不良导致的训练问题；

• 去掉全连接层，使网络变为全卷积网络；

• G网络中使用ReLU作为激活函数，最后一层使用tanh；

• D网络中使用LeakyReLU作为激活函数。

其中，转置卷积（也称反卷积）transposed conv或者deconv。

卷积置换如下图：

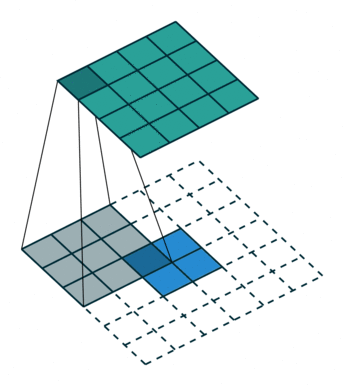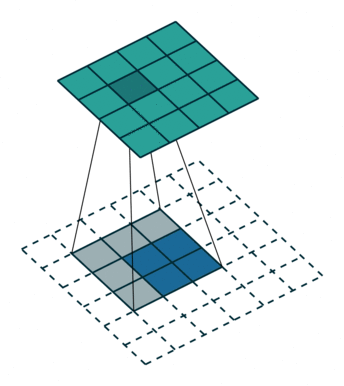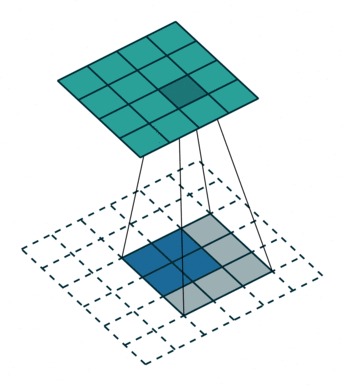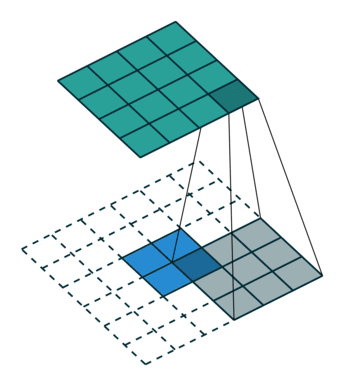
注意图中蓝色（下面）是输入，绿色（上面）是输出，卷积和反卷积在 $p、s、k$ 等参数一样时，是相当于 $i$ 和 $o$ 调了个位。 这里说明了反卷积的时候，是有补0的，即使人家管这叫no padding。图中反卷积应该从蓝色 2×2 扩展成绿色 4×4。

转置并不是指这个 3×3 的核 $w$ 变为 $w^T$，但如果将卷积计算写成矩阵乘法（在程序中，为了提高卷积操作的效率，就可以这么干，比如tensorflow中就是这种实现），而这样的矩阵乘法，恰恰等于 $w$ 左右翻转再上下翻转后与补0的 Y 卷积的情况。

DCGAN的核心是对CNN架构设置了一系列的约束来保证稳定的训练，具体限制如下：

• 在判别器中，把pooling层替换成strided convolutions；在生成器中，把pooling替换成fractional-strided convolutions。

• 在生成器和判别器中使用BN。这有助于解决由于初始化不良而导致的训练的问题，并有助于更深层次的模型中的梯度流动。

• 移除全连接层；

• 在生成器中，除输出之外的所有层使用ReLu，输出层使用Tanh激活函数。判别器中使用LeakyReLu激活函数。

对原始卷积神经网络进行了调整，以实现基于卷积网络的图像生成。

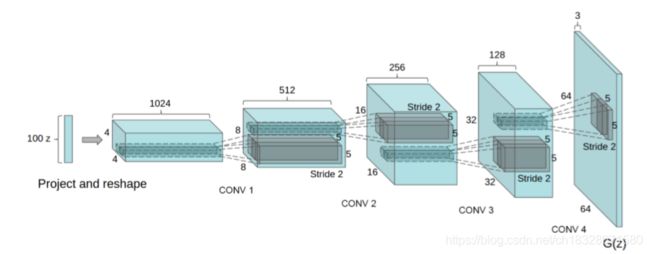
上图中，DCGAN生成器用于LSUN场景建模。将100维均匀分布Z投影到具有许多特征映射的小空间范围卷积表示。一系列的四个fractionally-strided convolutions将这种高级表示转换为64 x 64像素的图像。值得注意的是，没有使用全连接层或池化层。

随着来自生成图像模型的样本的视觉质量的提高，存在训练样本的过度拟合和记忆问题，即生成器有可能只是简单的记住样本，然后产生类似的输出结果。

DCGAN虽然有很好的架构，但是对GAN训练稳定性来说是治标不治本，没有从根本上解决问题，而且训练的时候仍需要小心的平衡G,D的训练进程，往往是训练一个多次，训练另一个一次。

三、WGAN

1、模型解析

与DCGAN不同，WGAN主要从损失函数的角度对GAN做了改进，损失函数改进之后的WGAN即使在全链接层上也能得到很好的表现结果，WGAN对GAN的改进主要有：

• 判别器最后一层去掉sigmoid；
• 生成器和判别器的loss不取log；
• 对更新后的权重强制截断到一定范围内，比如[-0.01，0.01]，以满足论文中提到的lipschitz连续性条件；
• 论文中也推荐使用SGD， RMSprop等优化器，不要基于使用动量的优化算法，比如adam，但是就我目前来说，训练GAN时，我还是adam用的多一些；

从上面看来，WGAN好像在代码上很好实现，基本上在原始GAN的代码上不用更改什么，但是它的作用是巨大的：

• WGAN理论上给出了GAN训练不稳定的原因，即交叉熵（JS散度）不适合衡量具有不相交部分的分布之间的距离，转而使用wassertein距离去衡量生成数据分布和真实数据分布之间的距离，理论上解决了训练不稳定的问题。
• 解决了模式崩溃的（collapse mode）问题，生成结果多样性更丰富。
• 对GAN的训练提供了一个指标，此指标数值越小，表示GAN训练的越差，反之越好。可以说之前训练GAN完全就和买彩票一样，训练好了算你中奖，没中奖也不要气馁，多买几注吧。有关GAN和WGAN的解释，可以参考链接：https://zhuanlan.zhihu.com/p/25071913

总的来说，GAN中交叉熵（JS散度）不适合衡量生成数据分布和真实数据分布的距离，如果通过优化JS散度训练GAN会导致找不到正确的优化目标，所以，WGAN提出使用wassertein距离作为优化方式训练GAN，但是数学上和真正代码实现上还是有区别的，使用Wasserteion距离需要满足很强的连续性条件—lipschitz连续性，为了满足这个条件，作者使用了将权重限制到一个范围的方式强制满足lipschitz连续性，但是这也造成了隐患，接下来会详细说。另外说实话，虽然理论证明很漂亮，但是实际上训练起来，以及生成结果并没有期待的那么好。

注：Lipschitz限制是在样本空间中，要求判别器函数D(x)梯度值不大于一个有限的常数K，通过权重值限制的方式保证了权重参数的有界性，间接限制了其梯度信息。

GAN与WGAN的对比如下图：

2、模型优点

1、不再需要纠结如何平衡Generator和Discriminator的训练程度，大大提高了GAN训练的稳定性：Critic（Discriminator）训练得越好，对提升Generator就越有利。

2、即使网络结构设计得比较简陋，WGAN也能展现出良好的性能，包括避免了mode collapse的现象，体现了出色的鲁棒性。

3、Critic的loss很准确地反映了Generator生成样本的质量，因此可以作为展现GAN训练进度的定性指标。

四、LSGAN

1、基本思想

LSGANs的英文全称是Least Squares GANs。这篇文章针对的是标准GAN生成的图片质量不高以及训练过程不稳定这两个缺陷进行改进。改进方法就是将GAN的目标函数由交叉熵损失换成最小二乘损失，而且这一个改变同时解决了两个缺陷。

为什么最小二乘损失可以提高生成图片质量？

GANs包含两个部分：判别器和生成器。判别器用于判断一张图片是来自真实数据还是生成器，要尽可能地给出准确判断；生成器用于生成图片，并且生成的图片要尽可能地混淆判别器。

本文作者认为以交叉熵作为损失，会使得生成器不会再优化那些被判别器识别为真实图片的生成图片，即使这些生成图片距离判别器的决策边界仍然很远，也就是距真实数据比较远。这意味着生成器的生成图片质量并不高。

为什么生成器不再优化优化生成图片呢？
是因为生成器已经完成我们为它设定的目标——尽可能地混淆判别器，所以交叉熵损失已经很小了。而最小二乘就不一样了，要想最小二乘损失比较小，在混淆判别器的前提下还得让生成器把距离决策边界比较远的生成图片拉向决策边界。这一段总结起来就是下图：

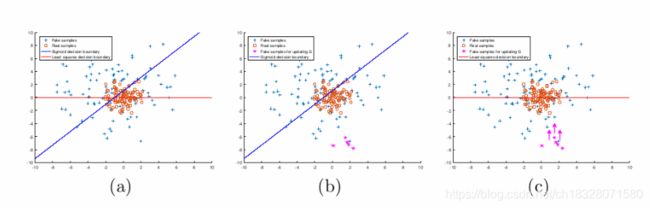
作者是把决策边界作为中介，认为生成图片和真实数据之间的距离可以由生成图片和决策边界之间的距离来反映。这是因为学到的决策边界必须穿过真实数据点，否则就是学习过程饱和了。在未来工作中作者也提到可以改进的一点就是直接把生成图片拉向真实数据，而不是拉向决策边界。

为什么最小二乘损失可以使得GAN的训练更稳定呢？
作者对这一点介绍的并不是很详细，只是说sigmoid交叉熵损失很容易就达到饱和状态（饱和是指梯度为0），而最小二乘损失只在一点达到饱和，如下图所示：

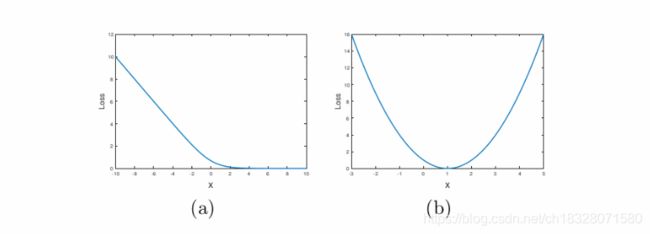
其中，(a)是交叉熵损失函数，(b)是最小二乘损失函数。

sigmoid损失处于饱和状态应该是和WGANs中提到的JS散度为常数一致，此时生成网络的梯度为0。

2、模型解析

事实上，作者认为使用JS散度并不能拉近真实分布和生成分布之间的距离，使用最小二乘可以将图像的分布尽可能的接近决策边界，其损失函数定义如下：

其中a,b,c满足：
$$b-c=1$$

$$b-a=2$$

下面介绍两种通用的a,b,c参数设置：

通过实验观察，作者发现 4 点技巧：

• 1、生成器 G 带有 batch normalization 批处理标准化（以下简称 BN）并且使用 Adam 优化器的话，LSGANs生成的图片质量好，但是传统 GANs 从来没有成功学习到，会出现 mode collapse 现象；
• 2、生成器 G 和判别器 D 都带有 BN 层，并且使用 RMSProp 优化器处理，LSGANs 会生成质量比 GANs 高的图片，并且 GANs 会出现轻微的 mode collapse 现象；
• 3、生成器 G 带有 BN 层并且使用 RMSProp 优化器，生成器 G 判别器 D 都带有 BN 层并且使用 Adam 优化器时，LSGANs 与传统 GANs 有着相似的表现；
• 4、RMSProp 的表现比 Adam 要稳定，因为传统 GANs 在 G 带有 BN 层时，使用 RMSProp 优化可以成功学习，但是使用 Adam 优化却不行。