python机器学习手写算法系列——GBDT梯度提升分类

梯度提升（Gradient Boosting）训练一系列的弱学习器（learners），每个学习器都针对前面的学习器的伪残差（而不是y），以此提升算法的表现（performance）。

维基百科是这样描述梯度提升的

梯度提升（梯度增强）是一种用于回归和分类问题的机器学习技术，其产生的预测模型是弱预测模型的集成，如采用典型的决策树 作为弱预测模型，这时则为梯度提升树（GBT或GBDT）。像其他提升方法一样，它以分阶段的方式构建模型，但它通过允许对任意可微分损失函数进行优化作为对一般提升方法的推广。

必要知识

1. 逻辑回归
2. 线性回归
3. 梯度下降
4. 决策树
5. 梯度提升回归

读完本文以后，您将会学会

1. 梯度提升如何运用于分类
2. 从零开始手写梯度分类

算法

下图很好的表现了梯度提升分类算法

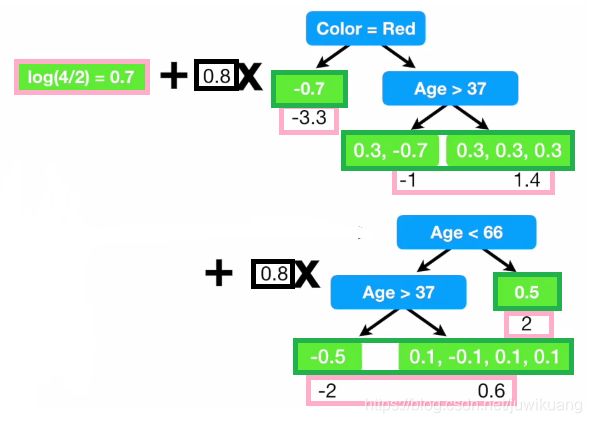
(图片来自Youtube频道StatQuest)

上图的第一部分是一个树桩，它的值是 log of odds of y， 我们记作$l$。后面跟着几棵树。后面的这些树，训练他们的时候，他们的目标并不是y，而是y的残差。

$$残差=真实值-预测值$$

这里的这张图，比梯度提升回归要复杂一点。这里，绿色的部分是残差，红色的是叫$\gamma$，黑色的是学习率。这里的残差并不是简单的平均一下求的$\gamma$。$\gamma$被用来更新$l$。

---

流程

Step 1: 计算log of odds $l_0$. 或者说这是y的第一次预测值. 这里 $n_1$ 是y=1的数量，$$n_0$$是y=0的数量。

$$l_0(x)=\log \frac{n_1}{n_0}$$

对于每个$x_i$, 概率是:
$$p_{0i}=\frac{e^{l_{0i}}}{1+e^{l_{0i}}}$$

预测值是:

$$f_{0i}=\{\begin{array}{ll}0& p_{0i}<0.5\\ 1& p_{0i}>=0.5\end{array}$$

Step 2 for m in 1 to M:

• Step 2.1: 计算所谓的伪残差：

$$r_{im}=f_i-p_i$$

• Step 2.2: 用伪残差拟合一颗回归树 $t_m(x)$ ，并识别出终点叶子节点 $R_{jm}$ for $j=1...Jm$
  

• Step 2.3: 计算每个叶子节点的 $\gamma$

$${\gamma }_{im}=\frac{\sum r_{im}}{\sum (1-r_{im-1})(r_{im-1})}$$

• Step 2.4: 更新$l$, $p$, $f$。 $\alpha$是学习率:
  $$l_m(x)=l_{m-1}+\alpha {\gamma }_m$$

$$p_{mi}=\frac{e^{l_{mi}}}{1+e^{l_{mi}}}$$

$$f_{mi}=\{\begin{array}{ll}0& p_{mi}<0.5\\ 1& p_{mi}>=0.5\end{array}$$
Step 3. 输出 $f_M(x)$

---

(Optional) 从梯度回归推导梯度回归分类

上面的简化流程的知识，对于手写梯度提升分类算法，已经足够了。如果有余力的，可以和我一起从梯度提升（GB）推理出梯度提升分类（GBC）

首先我们来看GB的步骤

---

梯度提升算法步骤

输入: 训练数据 $\{(x_i,y_i){\}}_{i=1}^n$, 一个可微分的损失函数 $L(y,F(x))$，循环次数M。

算法:

Step 1: 用一个常量$F_0(x)$启动算法，这个常量满足以下公式：

$$F_0(x)=\underset{\gamma }{\mathrm{argmin}}\sum _{i=1}^{n}L(y_i,\gamma )$$

Step 2: for m in 1 to M:

• Step 2.1: 计算伪残差（pseudo-residuals）:

$$r_{im}=-[\frac{\partial L(y_i,F(x_i))}{\partial F(x_i)}{]}_{F(x)=F_{m-1}(x)}$$

• Step 2.2: 用伪残差拟合弱学习器 $h_m(x)$ ，建立终点区域 $R_{jm}(j=1...J_m)$
  

• Step 2.3: 针对每个终点区域（也就是每一片树叶），计算 $\gamma$
  

$${\gamma }_{jm}=\underset{\gamma }{\mathrm{argmin}}\sum _{x_i\in R_{jm}}^{n}L(y_i,F_{m-1}(x_i)+\gamma )$$

• Step 2.4: 更新算法（学习率$\alpha$） :
  $$F_m(x)=F_{m-1}+\alpha {\gamma }_m$$

Step 3. 输出算法$$F_M(x)$$

---

损失函数

从梯度提升演绎到梯度提升分类，我们需要一个损失函数，并带入Step 1， Step 2.1 和 Step 2.3。这里，我们用 Log of Likelihood 作为损失函数。

$$L(y,F(x))=-\sum _{i=1}^N(y_i\ast log(p)+(1-y_i)\ast log(1-p))$$

这是一个关于概率p的函数，并不是关于log of odds （l）的函数，所以我们需要对其变形。

我们把中间部分拿出来
$$\begin{gathered} -(y\ast \log (p)+(1-y)\ast \log (1-p)) \\ =-y\ast \log (p)-(1-y)\ast \log (1-p) \\ =-y\log (p)-\log (1-p)+y\log (1-p) \\ =-y(\log (p)-\log (1-p))-\log (1-p) \\ =-y(\log (\frac{p}{1-p}))-\log (1-p) \\ =-y\log (odds)-\log (1-p) \end{gathered}$$
因为
$$\begin{gathered} \log (1-p)=log(1-\frac{e^{log(odds)}}{1+e^{log(odds)}}) \\ =\log (\frac{1+e^l}{1+e^l}-\frac{e^l}{1+e^l}) \\ =\log (\frac{1}{1+e^l}) \\ =\log (1)+\log (1+e^l) \\ =-log(1+e^{\log (odds)}) \end{gathered}$$

我们上面的带入，得到

$$\begin{gathered} -(y\ast \log (p)+(1-y)\ast \log (1-p)) \\ =-y\log (odds)+\log (1+e^{\log (odds)}) \end{gathered}$$

最后，我们得到了用$l$表示的损失函数

$$L=-\sum _{i=1}^N(yl-\log (1+e^l))$$

Step 1:

为了求损失函数的最小值，我们只需要求它的一阶导数等于0。
$$\begin{gathered} \frac{\partial L(y,F_0)}{\partial F_0} \\ =-\frac{\partial {\sum }_{i=1}^N(y\log (odds)-\log (1+e^{\log (odds)}))}{\partial log(odds)} \\ =-\sum _{i=1}^n{y}_i+\sum _{i=1}^N\frac{\partial log(1+e^{log(odds)})}{\partial log(odds)} \\ =-\sum _{i=1}^n{y}_i+\sum _{i=1}^N\frac{1}{1+e^{\log (odds)}}\frac{\partial (1+e^l)}{\partial l} \\ =-\sum _{i=1}^n{y}_i+\sum _{i=1}^N\frac{1}{1+e^{\log (odds)}}\frac{\partial (e^l)}{\partial l} \\ =-\sum _{i=1}^n{y}_i+\sum _{i=1}^N\frac{e^l}{1+e^l} \\ =-\sum _{i=1}^n{y}_i+N\frac{e^l}{1+e^l}=0 \end{gathered}$$
我们得到( p 是真实地概率)
$$\begin{gathered} \frac{e^l}{1+e^l}=\frac{{\sum }_{i=1}^N{y}_i}{N}=p \\ {e}^l=p+p\ast e^l \\ (1-p)e^l=p \\ {e}^l=\frac{p}{1-p} \\ \log (odds)=log(\frac{p}{1-p}) \end{gathered}$$

这里，我们就算出了$l$。

Step 2.1

$$r_{im}=-[\frac{\partial L(y_i,F(x_i))}{\partial F(x_i)}{]}_{F(x)=F_{m-1}(x)}$$

$$=-[\frac{\partial (-(y_i\ast log(p)+(1-y_i)\ast log(1-p)))}{\partial F_{m-1}(x_i)}{]}_{F(x)=F_{m-1}(x)}$$

类似地，可以得到

$$=y_i-F_{m-1}(x_i)$$

Step 2.3:

$${\gamma }_{jm}=\underset{\gamma }{\mathrm{argmin}}\sum _{x_i\in R_{jm}}^{n}L(y_i,F_{m-1}(x_i)+\gamma )$$

带入损失函数：

$$\begin{gathered} {\gamma }_{jm} \\ =\underset{\gamma }{\mathrm{argmin}}\sum _{x_i\in R_{jm}}^{n}L(y_i,F_{m-1}(x_i)+\gamma ) \\ =\underset{\gamma }{\mathrm{argmin}}\sum _{x_i\in R_{jm}}^n(-y_i\ast (F_{m-1}+\gamma )+\log (1+e^{F_{m-1}+\gamma })) \end{gathered}$$

我们来解中间部分。

$$-y_i\ast (F_{m-1}+\gamma )+\log (1+e^{F_{m-1}+\gamma })$$

我们用二阶泰勒多项展开式：

$$L(y,F+\gamma )\approx L(y,F)+\frac{dL(y,F+\gamma )\gamma }{dF}+\frac{1}{2}\frac{d^{2}L(y,F+\gamma ){\gamma }^2}{d^{2}F}$$

求导
$$\begin{gathered} \because \frac{dL(y,F+\gamma )}{d\gamma }\approx \frac{dL(y,F)}{dF}+\frac{d^{2}L(y,F)\gamma }{d^{2}F}=0 \\ \therefore \frac{dL(y,F)}{dF}+\frac{d^{2}L(y,F)\gamma }{d^{2}F}=0 \\ \therefore \gamma =-\frac{\frac{dL(y,F)}{dF}}{\frac{d^{2}L(y,F)}{d^{2}F}} \\ \therefore \gamma =\frac{y-p}{\frac{d^2(-y\ast l+\log (1+e^l))}{d^{2}l}} \\ \therefore \gamma =\frac{y-p}{\frac{d(-y+\frac{e^l}{1+e^l})}{dl}} \\ \therefore \gamma =\frac{y-p}{\frac{d\frac{e^l}{1+e^l}}{dl}} \end{gathered}$$
(用 product rule (ab)’=a’ b+a b’​)
$$\begin{gathered} \therefore \gamma =\frac{y-p}{\frac{d{e}^l}{dl}\ast \frac{1}{1+e^l}-e^l\ast \frac{d}{dl}\frac{1}{1+e^l}} \\ =\frac{y-p}{\frac{e^l}{1+e^l}-e^l\ast \frac{1}{(1+e^l{)}^2}\frac{d}{dl}(1+e^l)} \\ =\frac{y-p}{\frac{e^l}{1+e^l}-\frac{(e^l{)}^2}{(1+e^l{)}^2}} \\ =\frac{y-p}{e^l+(e^l{)}^2-+(e^l{)}^2} \\ =\frac{y-p}{\frac{e^l}{(1+e^l{)}^2}} \\ =\frac{y-p}{p(1-p)} \end{gathered}$$

最后得到$\gamma$如下

$$\gamma =\frac{\sum (y-p)}{\sum p(1-p)}$$

手写代码

先建立一张表，这里我们要预测一个人是否喜欢电影《Troll 2》。

no	name	likes_popcorn	age	favorite_color	loves_troll2
0	Alex	1	10	Blue	1
1	Brunei	1	90	Green	1
2	Candy	0	30	Blue	0
3	David	1	30	Red	0
4	Eric	0	30	Green	1
5	Felicity	0	10	Blue	1

Step 1 计算$l_0$, $p_0$, $f_0$

log_of_odds0=np.log(4 / 2)
probability0=np.exp(log_of_odds0)/(np.exp(log_of_odds0)+1)
print(f'the log_of_odds is : {log_of_odds0}')
print(f'the probability is : {probability0}')
predict0=1
print(f'the prediction is : 1')
n_samples=6

loss0=-(y*np.log(probability0)+(1-y)*np.log(1-probability0))

输出

the log_of_odds is : 0.6931471805599453
the probability is : 0.6666666666666666
the prediction is : 1

Step 2

我们先定义一个函数，我们叫他iteration，运行一次iteration就是跑一次for循环。把它拆开地目的就是为了让打架看清楚。

def iteration(i):
    #step 2.1 calculate the residuals
    residuals[i] = y - probabilities[i]
    #step 2.2 Fit a regression tree
    dt = DecisionTreeRegressor(max_depth=1, max_leaf_nodes=3)
    dt=dt.fit(X, residuals[i])
    
    trees.append(dt.tree_)
    
    #Step 2.3 Calculate gamma
    leaf_indeces=dt.apply(X)
    print(leaf_indeces)
    unique_leaves=np.unique(leaf_indeces)
    n_leaf=len(unique_leaves)
    #for leaf 1
    for ileaf in range(n_leaf):
        
        leaf_index=unique_leaves[ileaf]
        n_leaf=len(leaf_indeces[leaf_indeces==leaf_index])
        previous_probability = probabilities[i][leaf_indeces==leaf_index]
        denominator = np.sum(previous_probability * (1-previous_probability))
        igamma = dt.tree_.value[ileaf+1][0][0] * n_leaf / denominator
        gamma_value[i][ileaf]=igamma
        print(f'for leaf {leaf_index}, we have {n_leaf} related samples. and gamma is {igamma}')

    gamma[i] = [gamma_value[i][np.where(unique_leaves==index)] for index in leaf_indeces]
    #Step 2.4 Update F(x) 
    log_of_odds[i+1] = log_of_odds[i] + learning_rate * gamma[i]

    probabilities[i+1] = np.array([np.exp(odds)/(np.exp(odds)+1) for odds in log_of_odds[i+1]])
    predictions[i+1] = (probabilities[i+1]>0.5)*1.0
    score[i+1]=np.sum(predictions[i+1]==y) / n_samples
    #residuals[i+1] = y - probabilities[i+1]
    loss[i+1]=np.sum(-y * log_of_odds[i+1] + np.log(1+np.exp(log_of_odds[i+1])))
    
    new_df=df.copy()
    new_df.columns=['name', 'popcorn','age','color','y']
    new_df[f'$p_{i}$']=probabilities[i]
    new_df[f'$l_{i}$']=log_of_odds[i]
    new_df[f'$r_{i}$']=residuals[i]
    new_df[f'$\gamma_{i}$']=gamma[i]
    new_df[f'$l_{i+1}$']=log_of_odds[i+1]
    new_df[f'$p_{i+1}$']=probabilities[i+1]
    display(new_df)
    
    dot_data = tree.export_graphviz(dt, out_file=None, filled=True, rounded=True,feature_names=X.columns) 
    graph = graphviz.Source(dot_data) 
    display(graph)

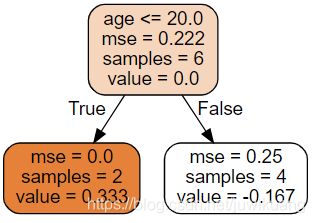
Iteration 0

iteration(0)

输出：

[1 2 2 2 2 1]
for leaf 1, we have 2 related samples. and gamma is 1.5
for leaf 2, we have 4 related samples. and gamma is -0.7499999999999998

no	name	popcorn	age	color	y	0	0	0	0	1	1
0	Alex	1	10	Blue	1	0.666667	0.693147	0.333333	1.50	1.893147	0.869114
1	Brunei	1	90	Green	1	0.666667	0.693147	0.333333	-0.75	0.093147	0.523270
2	Candy	0	30	Blue	0	0.666667	0.693147	-0.666667	-0.75	0.093147	0.523270
3	David	1	30	Red	0	0.666667	0.693147	-0.666667	-0.75	0.093147	0.523270
4	Eric	0	30	Green	1	0.666667	0.693147	0.333333	-0.75	0.093147	0.523270
5	Felicity	0	10	Blue	1	0.666667	0.693147	0.333333	1.50	1.893147	0.869114

我们分开来看每一个小步

Step 2.1, 计算残差 $y-p_0$.

Step 2.2, 拟合一颗回归树。

Step 2.3, 计算 $\gamma$.

• 对于叶子1, 我们有两个样本 (Alex 和 Felicity). $\gamma$ 是: (1/3+1/3)/((1-2/3)*2/3+(1-2/3)*2/3)=1.5

• 对于叶子2, 我们有四个样本. $\gamma$ 是:(1/3-2/3-2/3+1/3)/(4*(1-2/3)*2/3)=-0.75

Step 2.4, 更新F(x).

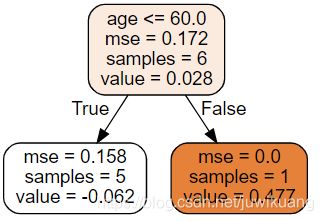
Iteration 1

iteration(1)

输出：

[1 2 1 1 1 1]
for leaf 1, we have 5 related samples. and gamma is -0.31564962030401844
for leaf 2, we have 1 related samples. and gamma is 1.9110594001952543

	name	popcorn	age	color	y	1	1	1	1	2	2
0	Alex	1	10	Blue	1	0.869114	1.893147	0.130886	-0.315650	1.640627	0.837620
1	Brunei	1	90	Green	1	0.523270	0.093147	0.476730	1.911059	1.621995	0.835070
2	Candy	0	30	Blue	0	0.523270	0.093147	-0.523270	-0.315650	-0.159373	0.460241
3	David	1	30	Red	0	0.523270	0.093147	-0.523270	-0.315650	-0.159373	0.460241
4	Eric	0	30	Green	1	0.523270	0.093147	0.476730	-0.315650	-0.159373	0.460241
5	Felicity	0	10	Blue	1	0.869114	1.893147	0.130886	-0.315650	1.640627	0.837620

对于树叶1，有5个样本。$\gamma$ 是：

(0.130886±0.523270±0.523270+0.476730+0.130886)/(20.869114(1-0.869114)+30.523270(1-0.523270))=-0.3156498224562022

对于树叶2，有1个样本。$\gamma$ 是：

0.476730/(0.523270*(1-0.523270))=1.9110593001700842

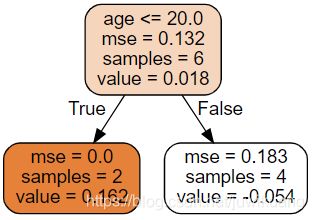
Iteration 2

iteration(2)

输出

no	name	popcorn	age	color	y	2	2	2	2	3	3
0	Alex	1	10	Blue	1	0.837620	1.640627	0.162380	1.193858	2.595714	0.930585
1	Brunei	1	90	Green	1	0.835070	1.621995	0.164930	-0.244390	1.426483	0.806353
2	Candy	0	30	Blue	0	0.460241	-0.159373	-0.460241	-0.244390	-0.354885	0.412198
3	David	1	30	Red	0	0.460241	-0.159373	-0.460241	-0.244390	-0.354885	0.412198
4	Eric	0	30	Green	1	0.460241	-0.159373	0.539759	-0.244390	-0.354885	0.412198
5	Felicity	0	10	Blue	1	0.837620	1.640627	0.162380	1.193858	2.595714	0.930585

Iteration 3 和 4 省略。。。

iteration(3)
iteration(4)

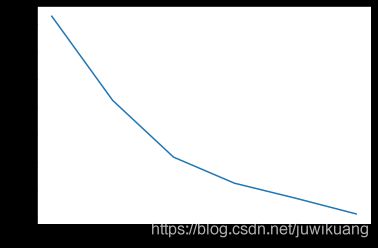
准确度:

损失:

代码地址：

https://github.com/EricWebsmith/machine_learning_from_scrach/blob/master/gradiant_boosting_classification.ipynb

引用

梯度提升 (维基百科)

Gradient Boost Part 3: Classification – Youtube StatQuest

Gradient Boost Part 4: Classification Details – Youtube StatQuest

sklearn.tree.DecisionTreeRegressor – scikit-learn 0.21.3 documentation

Understanding the decision tree structure – scikit-learn 0.21.3 documentation