深度学习--- GAN网络原理解析

Generative Adversarial Network对抗生成网络,这是当下机器视觉比较热门的一个技术,由两部分组成生成器($G_{net}$)和判别器($D_{net}$)组成

GAN区别与传统的生成网络,生成的图片还原度高,主要缘于D网络基于数据相对位置和数据本身对$real$数据奖励,对$fake$数据惩罚的缘故

1.GAN思想 & 与单个传统生成器和判别器的对比

1.1GAN的思想类似于"零和博弈",百度百科这样介绍:

零和游戏的原理如下：两人对弈，总会有一个赢，一个输，如果我们把获胜计算为得1分，而输棋为-1分。则若A获胜次数为N，B的失败次数必然也为N。若A失败的次数为M，则B获胜的次数必然为M。这样，A的总分为（N-M），B的总分为（M-N），显然（N-M）+（M-N）=0，这就是零和游戏的数学表达式。

也就是奖励获胜者,惩罚失败者,在GAN中就是奖励真实图片,且惩罚伪造图片,且奖励和惩罚同时发生,当然现在说这个有点早,往后看你会慢慢的发现这就是D网络的一个反馈机制

1.2单个生成器和判别器与GAN的对比

1.2.1 生成器(Generation)

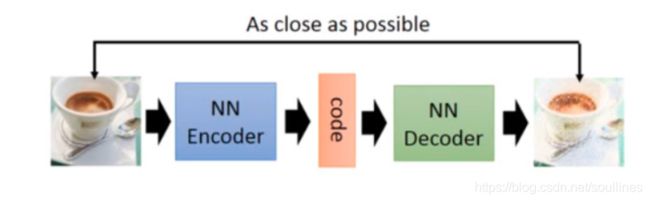
就是利用模型对图片的学习,最终达到可以自己生成图片的目的

就像上图表示的就是生成器的一种(还有一种变分自编码器这里不做过多的赘述)

$step1:$将图片传入解码器 NN-Encoder 转化为机器可以识别的array形式,然后通过 NN-Decoder生成图片 $Pi{c}_{fake}$

$step2:$已知真实图片 $Pi{c}_{real}$,通过$loss$函数$MSE$,计算真实图片和生成图片的$loss$,进而反馈网络

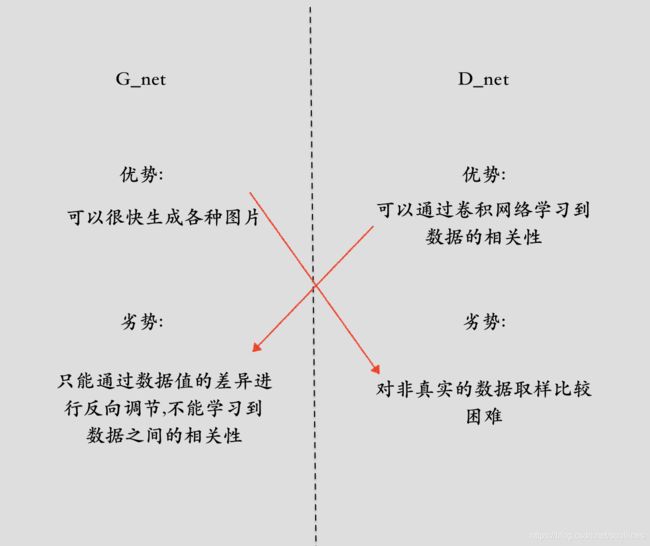
这样看起来好像是没有什么问题,但是需要注意一个问题,这里的$loss$仅仅计算数据之间的差异,图片的像素$val$不仅仅是数据的堆叠那么简单,同样相对位置(数据之间的相关性)也是很重要的一个部分,由于G网络没有办法学习到位置的相关性

所以$Generation$不能生成高还原度的图片

1.2.2 判别器(Discriminator)

简单来说就是一个判断 $real$图片和 $fake$图片的二分类模型

$input:xoutput:yy\in [0,1]$

Discriminator是一个卷积的神经网络,所以可以有效的区分图片的相对位置(即注重数据的相关性),但是由于Discriminator只对真实数据奖励(此时的$output$大),对伪造的数据惩罚(此时的$output$小)

所以随机数据的选取比较困难

这样对比下 G 和 D的优劣:

这样来看 G网络和 D网络各有优缺点,但是刚刚好可以互补,所以GAN网络顺势而生

2.GAN原理

2.1 Generation

由于单一G网络不能学习到数据之间的相关性,所以G网络的反向传播依赖于D网络

对于生成器而言,它的目的是Generation的$output$要无限接近于真实的数据分布:

这里会用到极大似然估计:

$step1:$给定真实的数据分布:$P_{data}$,G网络$output:x=G(z)$ ,这里的$z$是G网络的$intput$

$step2:$ 那么这个问题就变成一个求使G网络$output$无限接近于$P_{data}$这个真实分布的$\theta$的极大似然估计求解过程

这里我们用$P(x;\theta )$表示G网络$output$与$P_{data}$相似的概率,所以G网络就是求

$\forall \theta ;P(x;\theta )$最大 的过程;

下面是求解的过程:

${\theta }^{\ast }=argmax{\prod }_{i=1}^m{P}_G(x^i;\theta )=argmax{\sum }_{i=1}^{m}log(P_G(x^i;\theta ))$

​ $\approx argmax{E}_{x\sim p_{data}}[log(P_G(x^i;\theta ))]$

在这里我们要构建一个$KL-divergence$的形式,我们都知道个$KL-divergence$是描述两个概率之间差异的形式,上式后面加一个 ${\int }_x{P}_{data}(x)log(P_{data}(x)dx$ ,这是一个与$\theta$无关的项所以不会影响后序结果,却可以辅助构建$KL-divergence$形式,所以上式可以这样变形

上式 $=argmax[{\int }_x{P}_{data}(x)log(P_G(x^i;\theta ))-{\int }_x{P}_{data}(x)log(P_{data}(x)dx]$

​ $=argmaxKL(P_G||P_{data})$

​ $=argmniKL(P_{data}||P_G)$

这样看来G网络的计算就是求解$argmn{i}_{G}KL(P_{data}||P_G)$;但是$P_G$的分布和$P_{data}$的差异(也就是$P_{data}和P_G$的$KL-divergence$),G网络是没有完全办法计算的(G网络不具备数据相关性的学习能力),需要用到D网络的卷积来进行有效计算$loss$,所以接下来我们要引入D网络进行鉴别;

2.2 Discriminator

Discriminator鉴别器的机制是奖励真实样本,惩罚伪造样本,鉴别器需要获取G网络数据分布 $P_G$和真实数据分布$P_{data}$

• $step1:samplefrom{P}_{data}samplefrom{P}_G$
• $step2:$这样我们就获取到了$real$和$fake$的数据分布,用于D网络的$loss$计算

下面给出D网络的$loss$函数:

$V(G,D)=E_{x\sim p_{data}}[log(D(x))]+E_{x\sim p_G}[log(1-D(x))]$

这里简单赘述下,上面成本函数的计算过程,后面会详细提到:

V(G,D)可以看做是一个组合的$loss$函数

• 若$x$是生成的数据$x^{\sim }$,$P_{data}(x^{\sim })=0P_G(x^{\sim })=1$,那么:

  $V(G,D)=E_{x\sim p_G}[log(1-D(x^{\sim }))]$

• 若$x$是真实的数据$x$,$P_{data}(x)=1P_G(x)=0$,那么:

  $V(G,D)=E_{x\sim p_{data}}[log(D(x))]$

所以实际用到的:

$V(G,D)=E_{x\sim p_{data}}[log(D(x))]+E_{x^{\sim }\sim p_G}[log(1-D(x^{\sim }))]$

下面是求解的过程:

正如上面所说Discriminator鉴别器的机制是奖励真实样本,惩罚伪造样本;所以D网络的训练过程就是迭代计算使得其$loss$函数$V(G,D)$最大化的过程;也就是$argmaxV(D,G)$的过程;

为了方便计算出$V(G,D)$的最大值,我们求解最优的$D^{\ast }$(也就是$D(x)$),D网络运行阶段G网络可以看做是固定不变的;

$V(G,D)=E_{x\sim p_{data}}[log(D(x))]+E_{x\sim p_G}[log(1-D(x))]$

​ $={\int }_x{P}_{data}(x)logD(x)dx+{\int }_x{P}_G(x)log(1-D(x))dx$

​ $={\int }_x[P_{data}(x)logD(x)+{\int }_x{P}_G(x)log(1-D(x))]dx$

令 $a=P_{data}(x)D=D(x)b=P_G(x)$

则 $V(G,D)=alogD+blog(1-D)$

通过偏导来求上述公式的最大值:

$\frac{\partial V(G,D)}{\partial D}=\frac{a}{D}+\frac{b}{1-D}=0$

则: $D=a/a+b$

所以 $D^{\ast }=P_{data}(x)/(P_{data}(x)+P_G(x))$ 此为使$V(D,G)$最大化的最优解

代入$V(G,D)$

上式 $=V(G,D^{\ast })$

​ $=Ex\sim p_{data}[log\frac{P_{data}(x)}{P_{data}(x)+P_G(x)}]+Ex\sim p_G[log\frac{P_G(x)}{P_{data}(x)+P_G(x)}]$

​ $={\int }_x{P}_{data}(x)log\frac{P_{data}(x)}{P_{data}(x)+P_G(x)}dx+{\int }_x{P}_G(x)log\frac{P_G(x)}{P_{data}(x)+P_G(x)}dx$

​ $={\int }_x{P}_{data}(x)log\frac{P_{data}(x)}{\frac{P_{data}(x)+P_G(x)}{2}}\ast \frac{1}{2}dx+{\int }_x{P}_G(x)log\frac{P_G(x)}{\frac{P_{data}(x)+P_G(x)}{2}}\ast \frac{1}{2}dx$

​ $=-2log2+{\int }_x{P}_{data}(x)log\frac{P_{data}(x)}{\frac{P_{data}(x)+P_G(x)}{2}}dx+{\int }_x{P}_G(x)log\frac{P_G(x)}{\frac{P_{data}(x)+P_G(x)}{2}}dx$

这里需要提到J一个知识点:

• $JSDdivergence$ 是 $KLdivergence$ 的对称平滑版本，表示了两个分布之间的差异,上式没有办法转化为 $KL-divergence$.所以这里我们使用$JSD$

• $JSD$公式: $JSD(P||Q)=\frac{1}{2}D(P||M)+\frac{1}{2}D(Q||M)$ $M=\frac{1}{2}(P+Q)$

上式 $=-2log2+KL(P_{data}(x)||\frac{P_{data}(x)+P_G(x)}{2})+KL(P_G(x)||\frac{P_{data}(x)+P_G(x)}{2})$

​ $=-2log2+2JSD(P||Q)$

在数学中可以证明(这里不详细赘述),$JS{D}_{max}=log2$

所以$V(G,D)$最大值是0,最小值是$-2log2$;也就是说 $JSD$越大P和Q的差异越大,$JSD$越小P和Q的差异就越小

所以D网络最优的场景应当是:

$ma{x}_D(G,D)$最小的情况,此时$P_G=P_{data}$也就是生成数据完全与真实数据相等

综上来看,GAN就是 ${\theta }_G,{\theta }_D=argmi{n}_{G}ma{x}_{D}V(G,D)$的过程

3.GAN训练过程

这就是 GAN的整个训练过程,蓝色框是D网络的训练过程,红色框是G网络的训练过程

这里我们会注意到:

• D的$loss$迭代过程中要趋向于最大,所以${\theta }_d={\theta }_d+\eta \nabla loss$;
• G的$loss$迭代过程中要趋向于最小,所以${\theta }_d={\theta }_d-\eta \nabla loss$;
• 可以看出来一般情况下D网络每迭代多次,G网络仅迭代一次;主要原因G,D的反馈传播均依赖于D网络,G网络迭代一次,会让D网络的$loss$较之前下降,所以D网络要调节多次使得D网络的$loss$尽可能的大;
• D的$loss$可以看做对D网络而言分辨$real$数据和$fake$数据的损失,所以要最大化真实数据的期望$logD(x)$,同时最小化生成数据期望$logD(x^{\sim })$,也就是最大化$log(1-D(x^{\sim }))$,而 $los{s}_D=E_{x\sim p_{data}}[log(D(x))]+E_{x^{\sim }\sim p_G}[log(1-D(x^{\sim }))]$,所以D的期望是最大化$loss$
• 而G网络的$los{s}_G=E_{x^{\sim }\sim p_G}[log(1-D(x^{\sim }))]$,G网络的输入是没有$P_{data}$作为$input$,所以G网络仅保留V的后半部分,也可以看做一个类别的二分类器.是计算生成图片与目标图片的距离;所以越小越好

4.GAN的优化

我们先来看下G网络loss的图像:

可以看到 原始的G网络的$loss=log(1-D(x))$,首先我们知道我们初始化一般从0开始,而这个$loss$在0附近梯度较小,从0->1,梯度越来越大;这显然不符合我们的习惯,我们期望的模型迭代应当是初期梯度较大,随着$epoch$的增加梯度越来越小,这样有利于函数的收敛

所以我们可以把G网络的$loss$函数转化为$-log(D(x))$

以上是GAN基础学习中的一些感悟和整理,感谢阅读