【CV-Paper 19】图像分类 02：PReLU-Net-2015

论文原文：LINK
论文被引：9108(10/09/2020)

---

---

Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification

Abstract

Rectified activation units (rectifiers) are essential for state-of-the-art neural networks. In this work, we study rectifier neural networks for image classification from two aspects. First, we propose a Parametric Rectified Linear Unit (PReLU) that generalizes the traditional rectified unit. PReLU improves model fitting with nearly zero extra computational cost and little overfitting risk. Second, we derive a robust initialization method that particularly considers the rectifier nonlinearities. This method enables us to train extremely deep rectified models directly from scratch and to investigate deeper or wider network architectures. Based on our PReLU networks (PReLU-nets), we achieve 4.94% top-5 test error on the ImageNet 2012 classification dataset. This is a 26% relative improvement over the ILSVRC 2014 winner (GoogLeNet, 6.66% [29]). To our knowledge, our result is the firsttosurpasshuman-levelperformance (5.1%, [22]) on this visual recognition challenge.

整流激活单元（整流器）对于最新的神经网络至关重要。在这项工作中，我们从两个方面研究了用于图像分类的整流神经网络。首先，我们提出了一种参数化线性整流单元（PReLU），该参数化了传统的整流单元。 PReLU以几乎为零的额外计算成本和极小的过拟合风险改善了模型拟合。其次，我们得出了一种鲁棒的初始化方法，该方法特别考虑了整流器的非线性。这种方法使我们能够从头开始直接训练极深的整流模型，并研究更深或更广的网络结构。基于我们的PReLU网络（PReLU-net），我们在ImageNet 2012分类数据集上实现了4.94％的top-5测试错误。相对于2014年ILSVRC冠军（GoogLeNet，6.66％[29]），相对提高了26％。据我们所知，我们的结果是在这一视觉识别挑战上首次超过人类水平的表现（5.1％，[22]）。

---

1. Introduction

Convolutional neural networks (CNNs) [17, 16] have demonstrated recognition accuracy better than or comparable to humans in several visual recognition tasks, including recognizing traffic signs [3], faces [30, 28], and handwritten digits [3, 31]. In this work, we present a result that surpasses human-level performance on a more generic and challenging recognition task - the classification task in the 1000-class ImageNet dataset [22].

卷积神经网络（CNN）[17，16]在几种视觉识别任务中已表现出优于人类的识别精度，包括识别交通标志[3]，面部[30，28]和手写数字[3，31] 。在这项工作中，我们提出了一个结果，该结果在一个更通用和更具挑战性的识别任务上-在1000类ImageNet数据集中的分类任务[22]上，超过了人类水平的性能。

chnical directions: building more powerful models, and designing effective strategies against overfitting. On one hand, neural networks are becoming more capable of fitting training data, because of increased complexity (e.g., increased depth [25, 29], enlarged width [33, 24], and the use of smaller strides [33, 24, 2, 25]), new nonlinear activations [21, 20, 34, 19, 27, 9], and sophisticated layer designs [29, 11]. On the other hand, better generalization is achieved by effective regularization techniques [12, 26, 9, 31], aggressive data augmentation [16, 13, 25, 29], and large-scale data [4, 22].

技术方向：建立更强大的模型，并设计有效的策略以防止过拟合。一方面，由于复杂性增加（例如，深度[25，29]，宽度[33，24]，以及使用较小的步幅[33、24、2、25]，新的非线性激活[21、20、34、19、27、9]和复杂的层设计[29、11]。另一方面，通过有效的正则化技术[12、26、9、31]，积极的数据扩充[16、13、25、29]和大规模数据[4、22]，可以实现更好的泛化。

Among these advances, the rectifier neuron [21, 8, 20, 34], e.g., Rectified Linear Unit (ReLU), is one of several keys to the recent success of deep networks [16]. It expedites convergence of the training procedure [16] and leads to better solutions [21,8,20,34] than conventional sigmoidlike units. Despite the prevalence of rectifier networks, recent improvements of models [33, 24, 11, 25, 29] and theoretical guidelines for training them [7, 23] have rarely focused on the properties of the rectifiers.

在这些进步中，整流神经元[21、8、20、34]，例如，整流线性单元（Rectified Linear Unit ，ReLU），是深层网络最近取得成功的几个关键因素之一[16]。与传统的S形样单元相比，它加快了训练过程的收敛速度[16]，并实现了更好的解决方案[21,8,20,34]。尽管整流器网络很普遍，但是模型[33、24、11、25、29]的最新改进以及训练它们的理论指导[7、23]很少关注整流器的性能。

In this paper, we investigate neural networks from two aspects particularly driven by the rectifiers. First, we propose a new generalization of ReLU, which we call Parametric Rectified Linear Unit (PReLU). This activation function adaptively learns the parameters of the rectifiers, and improves accuracy at negligible extra computational cost. Second, we study the difficulty of training rectified models that are very deep. By explicitly modeling the nonlinearity of rectifiers (ReLU/PReLU), we derive a theoretically sound initialization method, which helps with convergence of very deep models (e.g., with 30 weight layers) trained directly from scratch. This gives us more flexibility to explore more powerful network architectures.

在本文中，我们从特别是由整流器驱动的两个方面研究了神经网络。首先，我们提出了ReLU的一种新的泛化，称为参数整流线性单元（Parametric Rectified Linear Unit，PReLU）。该激活函数可自适应地学习整流器的参数，并以可忽略的额外计算成本提高精度。其次，我们研究了训练深度模型的难度。通过对整流器（ReLU / PReLU）的非线性进行显式建模，我们导出了一种理论上合理的初始化方法，该方法有助于收敛从头开始直接训练的非常深的模型（例如，具有30个权重层）。这使我们拥有更大的灵活性来探索功能更强大的网络结构。

On the 1000-class ImageNet 2012 dataset, our PReLU network (PReLU-net) leads to a single-model result of 5.71% top-5 error, which surpasses all existing multi-model results. Further, our multi-model result achieves 4.94% top-5 error on the test set, which is a 26% relative improvement over the ILSVRC 2014 winner (GoogLeNet, 6.66% [29]). To the best of our knowledge, our result surpasses for the first time the reported human-level performance (5.1% in [22]) on this visual recognition challenge.

在1000类ImageNet 2012数据集上，我们的PReLU网络（PReLU-net）实现了5.71％的top-5误差的单模型结果，超过了所有现有的多模型结果。此外，我们的多模型结果在测试集上实现了5.94％的top-5错误，比ILSVRC 2014冠军（GoogLeNet，6.66％[29]）高26％。据我们所知，我们的结果首次超过了人类在视觉识别挑战方面的人类水平表现（在[22]中为5.1％）。

---

2. Approach

In this section, we first present the PReLU activation function (Sec. 2.1). Then we derive our initialization method for deep rectifier networks (Sec. 2.2). Lastly we discuss our architecture designs (Sec. 2.3).

在本节中，我们首先介绍PReLU激活功能（第2.1节）。然后，我们导出深层整流器网络的初始化方法（第2.2节）。最后，我们讨论我们的结构设计（第2.3节）。

2.1. Parametric Rectifiers

We show that replacing the parameter-free ReLU activation by a learned parametric activation unit improves classification accuracy.

我们表明，通过学习的参数激活单元替换无参数的ReLU激活可以提高分类精度。

Definition
Formally, we consider an activation function defined as:

Here yi is the input of the nonlinear activation f on the ith channel, and aiis a coefficient controlling the slope of the negative part. The subscript i in aiindicates that we allow the nonlinear activation to vary on different channels. When ai= 0, it becomes ReLU; when aiis a learnable parameter, we refer to Eqn.(1) as Parametric ReLU (PReLU). Figure 1 shows the shapes of ReLU and PReLU. Eqn.(1) is equivalent to $f(y_i)=max(0,y_i)+a_{i}min(0,y_i)$.

这里 $y_i$ 是第 $i$ 个通道上非线性激活 $f$ 的输入，并且是一个控制负半轴斜率的系数。下标 $i$ 表示我们允许非线性激活在不同通道上变化。当 $a_i=0$ 时，它成为ReLU；当 $a_i=0$ 是一个可学习参数时，我们将等式（1）称为参数ReLU（PReLU）。图1显示了ReLU和PReLU的形状。式（1）等于 $f(y_i)=max(0,y_i)+a_{i}min(0,y_i)$。

If $a_i$ is a small and fixed value, PReLU becomes the Leaky ReLU (LReLU) in [20] (ai= 0.01). The motivation of LReLU is to avoid zero gradients. Experiments in [20] show that LReLU has negligible impact on accuracy compared with ReLU. On the contrary, our method adaptively learns the PReLU parameters jointly with the whole model. We hope for end-to-end training that will lead to more specialized activations.

如果 $a_i$ 是一个小的固定值，则PReLU在[20]中将变为 Leaky ReLU（LReLU）（$a_i=0.01$），LReLU的动机是避免梯度为0。 [20]中的实验表明，与ReLU相比，LReLU对准确性的影响可忽略不计。相反，我们的方法与整个模型一起自适应地学习PReLU参数。我们希望进行端到端训练，这将实现更专业的激活。

PReLU introduces a very small number of extra parameters. The number of extra parameters is equal to the total number of channels, which is negligible when considering the total number of weights. So we expect no extra risk of overfitting. We also consider a channel-shared variant: $f(y_i)=max(0,y_i)+amin(0,y_i)$ where the coefficient is shared by all channels of one layer. This variant only introduces a single extra parameter into each layer.

PReLU引入了很少的额外参数。额外参数的数量等于通道的总数，在考虑权重的总数时可以忽略不计。因此，我们预计不会有过拟合风险。我们还考虑了通道共享的变体：$f(y_i)=max(0,y_i)+amin(0,y_i)$。其中，系数由一层的所有通道共享，此变体仅在每个层中引入一个额外的参数。

Optimization

PReLU can be trained using backpropagation [17] and optimized simultaneously with other layers. The update formulations of {ai} are simply derived from the chain rule. The gradient of ai for one layer is:

可以使用反向传播训练PReLU [17]，并与其他层同时进行优化。 {ai}的更新公式仅从链式法则中得出。一层的 $a_i$ 梯度为：

where $ϵ$ represents the objective function. The term $\frac{\partial E}{\partial f(yi)}$ is the gradient propagated from the deeper layer. The gradient of the activation is given by:

其中 $ϵ$ 表示目标函数。 $\frac{\partial E}{\partial f(yi)}$ 是从较深层传播的梯度。激活的梯度由下式给出：

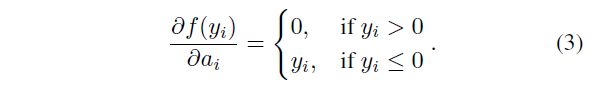
The summation ${\sum }_{y_i}$ runs over all positions of the feature map. For the channel-shared variant, the gradient of a is $\frac{\partial E}{\partial a}={\sum }_i{\sum }_{y_i}\frac{\partial E}{\partial f(y_i)}\frac{\partial f(y_i)}{\partial a}$, whereP isums over all channels of the layer. The time complexity due to PReLU is negligible for both forward and backward propagation. We adopt the momentum method when updating ai:

求和 ${\sum }_{y_i}$ 遍历特征图的所有位置。对于共享通道的变体，$a$ 的梯度为 $\frac{\partial E}{\partial a}={\sum }_i{\sum }_{y_i}\frac{\partial E}{\partial f(y_i)}\frac{\partial f(y_i)}{\partial a}$，其中 ${\sum }_i$在层的所有通道上求和。对于正向和反向传播，由于PReLU造成的时间复杂度可以忽略不计。我们在更新 $a_i$ 时采用动量法：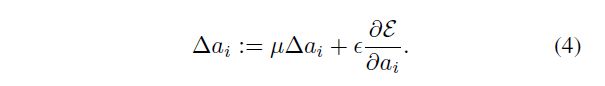
Here $\mu$ is the momentum and $ϵ$ is the learning rate. It is worth noticing that we do not use weight decay (l2 regularization) when updating $a_i$. A weight decay tends to push $a_i$ to zero, and thus biases PReLU toward ReLU. Even without regularization, the learned coefficients rarely have a magnitude larger than 1 in our experiments. Further, we do not constrain the range of $a_i$ so that the activation function may be non-monotonic. We use $a_i=0.25$ as the initialization throughout this paper.

这里的 $\mu$ 是动量，而 $ϵ$ 是学习率。值得注意的是，在更新 $a_i$ 时，我们不使用权重衰减（l2 regularization）。权重衰减倾向于将 $a_i$ 置零，从而使PReLU偏向ReLU。即使没有正则化，在我们的实验中，学习的系数也很少有大于1的量级。此外，我们不限制 $a_i$ 的范围，以使激活函数可以是非单调的。在本文中，我们将 $a_i=0.25$ 用作初始化。

Comparison Experiments

We conducted comparisons on a deep but efficient model with 14 weight layers. The model was studied in [10] (model E of [10]) and its architecture is described in Table 1. We choose this model because it is sufficient for representing a category of very deep models, as well as to make the experiments feasible.

我们对具有14个权重层的深而有效的模型进行了比较。在[10]中研究了该模型（[10]的模型E），其结构在表1中进行了描述。我们选择此模型是因为它足以代表一类非常深的模型，并且使实验可行。

As a baseline, we train this model with ReLU applied in the convolutional (conv) layers and the first two fullyconnected (fc) layers. The training implementation follows [10]. The top-1 and top-5 errors are 33.82% and 13.34% on ImageNet 2012, using 10-view testing (Table 2).

作为基线，我们使用在卷积（conv）层和前两个全连接（fc）层中应用ReLU训练该模型。训练实施如下[10]。使用10个视图测试（表2），ImageNet 2012的top-1和top-5错误分别为33.82％和13.34％。

表1.一个小而深的14层模型[10]。列出了每层的滤波器尺寸和滤波器编号。数字 /s 表示使用的步幅s。还显示了PReLU的学习系数。对于逐个通道的情况，显示了每一层的通道上{ai}的平均值。

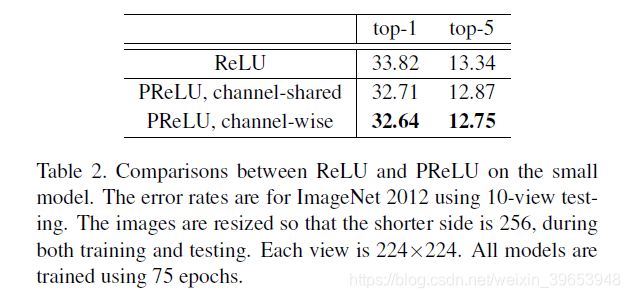
表2.小型模型上的ReLU和PReLU之间的比较。错误率适用于使用10视图测试的ImageNet 2012。调整图像大小，以便在训练和测试期间较短的边为256。每个视图为224×224。所有模型都使用75个epoch进行训练。

Then we train the same architecture from scratch, with all ReLUs replaced by PReLUs (Table 2). The top-1 error is reduced to 32.64%. This is a 1.2% gain over the ReLU baseline. Table 2 also shows that channel-wise/channelshared PReLUs perform comparably. For the channelshared version, PReLU only introduces 13 extra free parameters compared with the ReLU counterpart. But this small number of free parameters play critical roles as evidenced by the 1.1% gain over the baseline. This implies the importance of adaptively learning the shapes of activation functions.

然后，我们从头开始训练相同的结构，所有ReLU被PReLU取代（表2）。top-1错误减少到32.64％，这比ReLU基准提高了1.2％。表2还显示了按通道/按通道共享的PReLU的性能相当。对于通道共享版本，与ReLU相比，PReLU仅引入了13个额外的免费参数。但是，如此少量的自由参数起着至关重要的作用，这比基线提高了1.1％证明了这一点。这意味着自适应学习激活函数形状的重要性。

Table 1 also shows the learned coefficients of PReLUs for each layer. There are two interesting phenomena in Table 1. First, the first conv layer (conv1) has coefficients (0.681 and 0.596) significantly greater than 0. As the filters of conv1 are mostly Gabor-like filters such as edge or texture detectors, the learned results show that both positive and negative responses of the filters are respected. We believe that this is a more economical way of exploiting lowlevel information, given the limited number of filters (e.g., 64). Second, for the channel-wise version, the deeper conv layers in general have smaller coefficients. This implies that the activations gradually become “more nonlinear” at increasing depths. In other words, the learned model tends to keep more information in earlier stages and becomes more discriminative in deeper stages.

表1还显示了每一层的PReLU的学习系数。表1中有两个有趣的现象。首先，第一conv层（conv1）的系数（0.681和0.596）显着大于0。由于conv1的滤波器主要是类似Gabor的滤波器，例如边缘或纹理检测器，因此结果表明，滤波器的正响应和负响应都得到了尊重。我们认为，鉴于滤波器数量有限（例如64个），这是一种利用低级信息的更经济的方式。其次，对于通道方式版本，较深的conv层通常具有较小的系数。这意味着，随着深度的增加，激活逐渐变得“非线性”。换句话说，学习型模型倾向于在早期阶段保留更多信息，而在较深阶段则更具区分性。

2.2. Initialization of Filter Weights for Rectifiers

Rectifier networks are easier to train [8, 16, 34] compared with traditional sigmoid-like activation networks. But a bad initialization can still hamper the learning of a highly non-linear system. In this subsection, we propose a robust initialization method that removes an obstacle of training extremely deep rectifier networks.

与传统的S形激活网络相比，整流器网络更容易训练[8、16、34]。但是，不良的初始化仍然会阻碍高度非线性系统的学习。在本小节中，我们提出了一种鲁棒的初始化方法，该方法消除了训练极深的整流器网络的障碍。

Recent deep CNNs are mostly initialized by random weights drawn from Gaussian distributions [16]. With fixed standard deviations (e.g., 0.01 in [16]), very deep models (e.g., >8 conv layers) have difficulties to converge, as reported by the VGG team [25] and also observed in our experiments. To address this issue, in [25] they pre-train a model with 8 conv layers to initialize deeper models. But this strategy requires more training time, and may also lead to a poorer local optimum. In [29, 18], auxiliary classifiers are added to intermediate layers to help with convergence.

最近的深层CNN大多通过从高斯分布中提取的随机权重来初始化[16]。如VGG小组[25]所述，并且在我们的实验中也观察到，在固定标准差（例如[16]中的0.01）的情况下，非常深的模型（例如 > 8个卷积层）难以收敛。为了解决这个问题，在[25]中，他们预训练了具有8个卷积层的模型以初始化更深的模型。但是这种策略需要更多的训练时间，并且还可能导致较差的局部最优值。在[29，18]中，辅助分类器被添加到中间层以帮助收敛。

Glorot and Bengio [7] proposed to adopt a properly scaled uniform distribution for initialization. This is called “Xavier” initialization in [14]. Its derivation is based on the assumption that the activations are linear. This assumption is invalid for ReLU and PReLU.

Glorot和Bengio [7]提出采用适当缩放的均匀分布进行初始化。在[14]中这被称为 “Xavier”初始化。它的推导基于激活是线性的假设，该假设对ReLU和PReLU无效。

In the following, we derive a theoretically more sound initialization by taking ReLU/PReLU into account. In our experiments, our initialization method allows for extremely deep models (e.g., 30 conv/fc layers) to converge, while the “Xavier” method [7] cannot.

在下文中，我们通过考虑ReLU / PReLU得出理论上更合理的初始化。在我们的实验中，我们的初始化方法允许极深的模型（例如30个conv/fc层）收敛，而 “Xavier” 方法[7]则不能。

Forward Propagation Case

Our derivation mainly follows [7]. The central idea is to investigate the variance of the responses in each layer. For a conv layer, a response is:

我们的推导主要遵循[7]。中心思想是调查每一层响应的方差。对于卷积层，响应为：

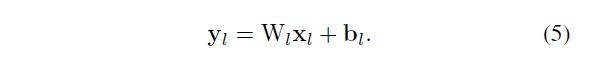
Here, $x$ is a $k^{2}c-by-1$ vector that represents co-located $k\times k$ pixels in c input channels. $k$ is the spatial filter size of the layer. With $n=k2c$ denoting the number of connections of a response, W is a d-by-n matrix, where d is the number of filters and each row of W represents the weights of a filter. b is a vector of biases, and $y$ is the response at a pixel of the output map. We use $l$ to index a layer. We have $x_l=f(y_l-1)$ where $f $ is the activation. We also have $c_l=d_{l-1}$.

在此，$x$ 是一个 $k^{2}c\times 1$ 向量，表示在 $c$ 个输入通道中并置的 $k\times k$ 个像素。 $k$ 是图层的空间滤波器大小。其中 $n=k^{2}c$ 表示响应的连接数，$W$ 是 $d\times n$ 矩阵，其中 $d$ 是滤波器的数量，$W$ 的每一行代表滤波器的权重。 $b$ 是偏差的向量，$y$ 是在输出图的像素处的响应。我们使用 $l$ 索引图层。我们有 $x_l=f(y_l-1)$，其中 $f$ 是激活。我们也有 $c_l=d_{l-1}$。

We let the initialized elements in $W_l$ be mutually independent and share the same distribution. As in [7], we assume that the elements in $x_l$ are also mutually independent and share the same distribution, and $x_l$ and $W_l$ are independent of each other. Then we have:

我们让 $W_l$ 中的初始化元素相互独立并共享相同的分布。与[7]中一样，我们假设 $x_l$ 中的元素也相互独立并且共享相同的分布，并且 $x_l$ 和 $W_l$ 彼此独立。然后我们有：

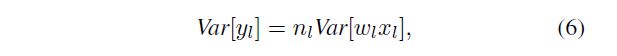
where now $y_l$, $x_l$, and $w_l$ represent the random variables of each element in $y_l$, $W_l$, and $x_l$ respectively. We let wl have zero mean. Then the variance of the product of independent variables gives us:

现在 $y_l$, $x_l$, $w_l$ 分别代表 $y_l$, $W_l$, $x_l$ 中每个元素的随机变量。我们让 $w_l$ 的均值为零。然后，自变量乘积的方差给出：

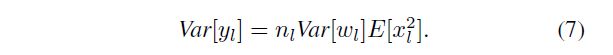
Here $E[x_l^2]$ is the expectation of the square of $x_l$. It is worth noticing that $E[x_l^2]\ne Var[x_l]$ unless $x_l$ has zero mean. For the ReLU activation, $x_l=max(0,y_{l-1})$ and thus it does not have zero mean. This will lead to a conclusion different from [7].

这里 $E[x_l^2]$ 是 $x_l$ 平方的期望。值得注意的是，除非 $x_l$ 的均值为零，否则 $E[x_l^2]\ne Var[x_l]$ 。对于ReLU激活，$x_l=max(0,y_{l-1})$，因此没有零均值。这将得出与[7]不同的结论。

If we let $w_{l-1}$ have a symmetric distribution around zero and $b_{l-1}=0$, then $y_{l-1}$ has zero mean and has a symmetric distribution around zero. This leads to $E[x_l^2]=\frac{1}{2}Var[y_l-1]$ when $f$ is ReLU. Putting this into Eqn.(7), we obtain:

如果让 $w_{l-1}$ 在零附近具有对称分布并且 $b_{l-1}=0$，则 $y_{l-1}$ 的均值将为零并且在零附近具有对称的分布。当 $f$ 是ReLU时，这导致 $E[x_l^2]=\frac{1}{2}Var[y_l-1]$。将其放入等式（7），我们得到：

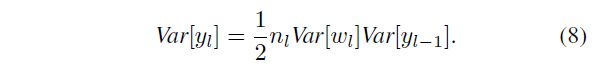
With L layers put together, we have:

This product is the key to the initialization design. A proper initialization method should avoid reducing or magnifying the magnitudes of input signals exponentially. So we expect the above product to take a proper scalar (e.g., 1). A sufficient condition is:

该产品是初始化设计的关键。适当的初始化方法应避免按指数形式减小或放大输入信号的幅度。因此，我们希望上述乘积具有适当的标量（例如1）。一个充分的条件是：

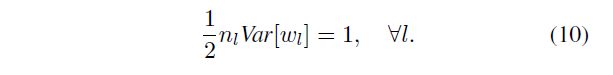
This leads to a zero-mean Gaussian distribution whose standard deviation (std) is $\sqrt{2/n_l}$. This is our way of initialization. We also initialize $b=0$.

这导致零均值高斯分布，其标准差（std）为 $\sqrt{2/n_l}$，这是我们的初始化方式，我们还初始化 $b=0$。

For the first layer ($l=1$), we should have $n_{1}Var[w_1]=1$ because there is no ReLU applied on the input signal. But the factor $1/2$ does not matter if it just exists on one layer. So we also adopt Eqn.(10) in the first layer for simplicity.

对于第一层（$l=1$），我们应该具有 $n_{1}Var[w_1]=1$，因为在输入信号上没有施加ReLU。但是，如果因子 $1/2$ 仅存在于一层上，则无关紧要。因此，为简单起见，我们在第一层也采用等式（10）。

Backward Propagation Case

For back-propagation, the gradient of a conv layer is computed by:

Here we use $∆x$ and $∆y$ to denote gradients ($\frac{\partial E}{\partial x}$ and $\frac{\partial E}{\partial y}$) for simplicity. $∆y$ represents k-by-k pixels in $d$ channels, and is reshaped into a $k^{2}d-by-1$ vector. We denote $\hat{n}=k^{2}d$. Note that $\hat{n}\ne n=k^{2}c$. $W$ is a $c-by-\hat{n}$ matrix where the filters are rearranged in the way of back-propagation. Note that $W$ and $\hat{W}$ can be reshaped from each other. $∆x$ is a $c-by-1$ vector representing the gradient at a pixel of this layer. As above, we assume that $w_l$ and $∆y_l$ are independent of each other, then $∆x_l$ has zero mean for all $l$, when $w_l$ is initialized by a symmetric distribution around zero.

在这里，为简单起见，我们使用 $∆x$ 和 $∆y$ 表示梯度（$\frac{\partial E}{\partial x}$ 和 $\frac{\partial E}{\partial y}$）。$∆y$ 代表 $d$ 通道中的 $k\times k$ 像素，并重塑为 $k^{2}d-by-1$ 向量。我们表示 $\hat{n}=k^{2}d$ 。注意 $\hat{n}\ne n=k^{2}c$ 是一个 $c-by-\hat{n}$ 矩阵，其中的滤波器以反向传播的方式重新排列。请注意，$W$ 和 $\hat{W}$ 可以彼此重塑。 $∆x$ 是 $c-by-1$向量，代表该层像素上的梯度。如上所述，我们假设 $w_l$ 和 $∆y_l$ 彼此独立，那么当 $w_l$ 由零附近的对称分布初始化时，$∆x_l$ 的所有 $l$ 均值为零。

In back-propagation we also have $∆y_l=f^{\prime }(y_l)∆x_{l+1}$ where $f^{\prime }$ is the derivative of $f$. For the ReLU case, $f^{\prime }(y_l)$ is zero or one, and their probabilities are equal. We assume that $f^{\prime }(y_l)$ and $∆x_{l+1}$ are independent of each other. Thus we have $E[∆y_l]=E[∆x_{l+1}]/2=0$, and also $E[(∆y_l{)}^2]=Var[∆y_l]=1/2Var[∆x_{l+1}]$. Then we compute the variance of the gradient in Eqn.(11):

在反向传播中，我们还有 $∆y_l=f^{\prime }(y_l)∆x_{l+1}$，其中 $f^{\prime }$ 是 $f$ 的导数。对于ReLU，$f^{\prime }(y_l)$ 为零或一，并且它们的概率相等。我们假设 $f^{\prime }(y_l)$ 和 $∆x_{l+1}$ 彼此独立。因此，我们有 $E[∆y_l]=E[∆x_{l+1}]/2=0$，还有 $E[(∆y_l{)}^2]=Var[∆y_l]=1/2Var[∆x_{l+1}]$。然后我们在等式（11）中计算梯度的方差：

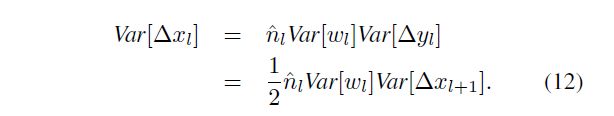
The scalar $1/2$ in both Eqn.(12) and Eqn.(8) is the result of ReLU, though the derivations are different. With $L$ layers put together, we have:

式（12）和式（8）中的标量 $1/2$ 都是ReLU的结果，尽管推导是不同的。将 $L$ 层放在一起，我们得到：

We consider a sufficient condition that the gradient is not exponentially large/small:

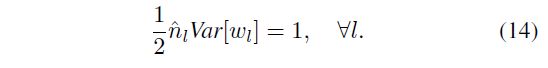
The only difference between this equation and Eqn.(10) is that ${\hat{n}}_l=k_l^2{d}_l$ while $n_l=k_l^2{c}_l=k_l^2{d}_{l-1}$. Eqn.(14) results in a zero-mean Gaussian distribution whose std is $\sqrt{2/{\hat{n}}_l}$.

该方程式与公式（10）的唯一区别是 ${\hat{n}}_l=k_l^2{d}_l$ 而 $n_l=k_l^2{c}_l=k_l^2{d}_{l-1}$。等式（14）得到一个零均值高斯分布，其std为 $\sqrt{2/{\hat{n}}_l}$。

For the first layer ($l=1$), we need not compute ∆x1 because it represents the image domain. But we can still adopt Eqn.(14) in the firstlayer, for the same reasonas in the forward propagation case - the factor of a single layer does not make the overall product exponentially large/small.

对于第一层（$l=1$），我们无需计算 $∆x_1$，因为它表示图像域。但是，由于与正向传播情况相同的原因，我们仍可以在第一层采用等式（14）-单层的因子不会使整体乘积成倍增大或减小。

We note that it is sufficient to use either Eqn.(14) or Eqn.(10) alone. For example, if we use Eqn.(14), then in Eqn.(13) the product ${\prod }_{l=2}^L\frac{1}{2}{\hat{n}}_{l}Var[w_l]=1$, and in Eqn.(9) the product ${\prod }_{l=2}^L\frac{1}{2}{n}_{l}Var[w_l]={\prod }_{l=2}^L{n}_l/{\hat{n}}_l=c_2/d_L$, which is not a diminishing number in common network designs. This means that if the initialization properly scales the backward signal, then this is also the case for the forward signal; and vice versa. For all models in this paper, both forms can make them converge.

我们注意到，单独使用等式（14）或等式（10）就足够了。例如，如果我们使用等式（14），则在等式（13）中，${\prod }_{l=2}^L\frac{1}{2}{\hat{n}}_{l}Var[w_l]=1$，在等式（9）中，${\prod }_{l=2}^L\frac{1}{2}{n}_{l}Var[w_l]={\prod }_{l=2}^L{n}_l/{\hat{n}}_l=c_2/d_L$，这在普通网络设计中不是一个递减的数字。这意味着，如果初始化正确地缩放了后向信号，则前向信号也是如此；反之亦然。对于本文中的所有模型，两种形式都可以使它们收敛。

Discussions
If the forward/backward signal is inappropriately scaled by a factor $\beta$ in each layer, then the final propagated signal will be rescaled by a factor of ${\beta }^L$ after L layers, where $L$ can represent some or all layers. When $L$ is large, if $\beta >1$, this leads to extremely amplified signals and an algorithm output of infinity; if $\beta <1$, this leads to diminishing signals. In either case, the algorithm does not converge - it diverges in the former case, and stalls in the latter.

如果前向/后向信号在每层中不适当地按因子 $\beta$ 缩放，则最终的传播信号将在 $L$ 层之后按 ${\beta }^L$ 因子重新缩放，其中 $L$ 可以代表部分或全部层。当 $L$ 大时，如果 $\beta >1$，则将导致极大的信号放大，并产生无穷大的算法输出。如果 $\beta <1$，则导致信号减弱。无论哪种情况，算法都不会收敛-在前一种情况下会发散，而在后一种情况下会停滞。

Our derivation also explains why the constant standard deviation of 0.01 makes some deeper networks stall [25]. We take “model B” in the VGG team’s paper [25] as an example. This model has 10 conv layers all with 3×3 filters. The filter numbers ($d_l$) are 64 for the 1st and 2nd layers, 128 for the 3rd and 4th layers, 256 for the 5th and 6th layers, and 512 for the rest. The std computed by Eqn.(14) (KaTeX parse error: Expected '}', got 'EOF' at end of input: …rt{2/ \hat{n}_l) is 0.059, 0.042, 0.029, and 0.021 when the filter numbers are 64, 128, 256, and 512 respectively. If the std is initialized as 0.01, the std of the gradient propagated from conv10 to conv2 is 1/(5.9 × 4.22× 2.92× 2.14) = 1/(1.7 × 104) of what we derive. This number may explain why diminishing gradients were observed in experiments.

我们的推导也解释了为什么恒定的 $0.01$ 标准差会使一些更深的网络停滞[25]。我们以VGG小组论文[25]中的“模型B”为例。该模型有10个卷积层，全部带有3×3滤波器。第一层和第二层的过滤器编号（$d_l$）为64，第三层和第四层的滤波器编号为128，第五层和第六层的滤波器编号为256，其余的为512。当滤波器数分别为64、128、256和512时，由等式（14）（$\sqrt{2/{\hat{n}}_l}$）计算的std为0.059、0.042、0.029和0.021。如果将std初始化为0.01，则从conv10传播到conv2的梯度的std等于所导出结果的1 /（5.9×4.22×2.92×2.14）= 1 /（1.7×104）。这个数字可以解释为什么在实验中观察到梯度递减。

It is also worth noticing that the variance of the input signal can be roughly preserved from the first layer to the last. In cases when the input signal is not normalized (e.g., it is in the range of $[-128,128]$), its magnitude can be so large that the softmax operator will overflow. A solution is to normalize the input signal, but this may impact other hyper-parameters. Another solution is to include a small factor on the weights among all or some layers, e.g., ${}^L\sqrt{1/128}$ on L layers. In practice, we use a std of 0.01 for the first two fc layers and 0.001 for the last. These numbers are smaller than they should be (e.g., $\sqrt{2/4096}$) and will address the normalization issue of images whose range is about [−128,128].

还值得注意的是，从第一层到最后一层可以大致保留输入信号的方差。在未对输入信号进行归一化的情况下（例如，它在 $[-128,128]$ 范围内），其大小可能太大，以至于softmax运算符将溢出。解决方案是对输入信号进行归一化，但这可能会影响其他超参数。另一解决方案是在所有或一些层之间的重量上包括小的因素，例如，L层上的 ${}^L\sqrt{1/128}$。在实践中，我们将前两个fc层的std设置为0.01，最后一个0.001。这些数字小于应有的数字（例如 $\sqrt{2/4096}$），并将解决范围约为 $[-128,128]$ 的图像的标准化问题。

For the initialization in the PReLU case, it is easy to show that Eqn.(10) becomes:

where $a$ is the initialized value of the coefficients. If $a=0$, it becomes the ReLU case; if $a=1$, it becomes the linear case (the same as [7]). Similarly, Eqn.(14) becomes $\frac{1}{2}(1+a^2){\hat{n}}_{l}Var[w_l]=1$.

其中a是系数的初始化值。如果 $a=0$，则成为ReLU情况；如果 $a=1$，则成为线性情况（与[7]相同）。类似地，等式（14）变为 $\frac{1}{2}(1+a^2){\hat{n}}_{l}Var[w_l]=1$。

Comparisons with “Xavier” Initialization [7]

The main difference between our derivation and the “Xavier” initialization [7] is that we address the rectifier nonlinearities3. The derivation in [7] only considers the linear case, and its result is given by $n_{l}Var[w_l]=1$ (the forward case), which can be implemented as a zero-mean Gaussian distribution whose std is $\sqrt{1/n_l}$. When there are L layers, the std will be $1/{\sqrt{2}}^L$ of our derived std. This number, however, is not small enough to completely stall the convergence of the models actually used in our paper (Table 3, up to 22 layers) as shown by experiments. Figure 2 compares the convergence of a 22-layer model. Both methods are able to make them converge. But ours starts reducing error earlier. We also investigate the possible impact on accuracy. For the model in Table 2 (using ReLU), the “Xavier” initialization method leads to 33.90/13.44 top1/top-5 error, and ours leads to 33.82/13.34. We have not observed clear superiority of one to the other on accuracy.

我们的推导和“ Xavier”初始化[7]之间的主要区别是我们解决了整流器的非线性问题3。 [7]中的推导仅考虑线性情况，其结果由 $n_{l}Var[w_l]=1$（正向情况）给出，可以将其实现为零均值高斯分布，其std为 $\sqrt{1/n_l}$。当有 $L$ 层时，std将是我们导出的std的 $1/{\sqrt{2}}^L$。然而，这个数字还不足以完全阻止我们的论文中实际使用的模型（表3，最多22层）的收敛，如实验所示。图2比较了22层模型的收敛性。两种方法都能使它们收敛。但是我们更早开始减少错误。我们还将调查对准确性的可能影响。对于表2中的模型（使用ReLU），“Xavier” 初始化方法会导致33.90/13.44 top1/top-5错误，而我们的则会导致33.82/13.34。我们还没有观察到在准确性方面一个明显的优势。

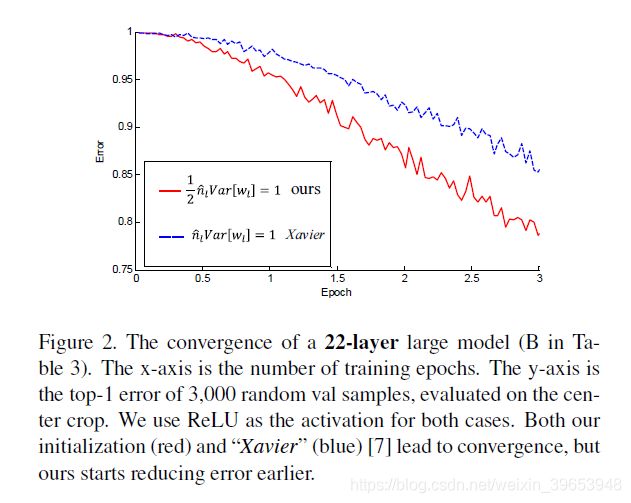
图2. 22层大型模型的收敛性（表3中的B）。 x轴是训练时期的数量。 y轴是在中心作物上评估的3,000个随机val样本的top-1误差。对于这两种情况，我们都使用ReLU作为激活。我们的初始化（红色）和“ Xavier”（蓝色）[7]都导致收敛，但是我们的初始化开始降低误差。

Next, we compare the two methods on extremely deep models with up to 30 layers (27 conv and 3 fc). We add up to sixteen conv layers with 256 2×2 filters in the model in Table 1. Figure 3 shows the convergence of the 30-layer model. Our initialization is able to make the extremely deep model converge. On the contrary, the “Xavier” method completely stalls the learning, and the gradients are diminishing as monitored in the experiments.

接下来，我们在具有30层（27转化和3 fc）的超深度模型上比较这两种方法。在表1的模型中，我们最多使用16个conv层和256个2×2滤波器。图3显示了30层模型的收敛性。我们的初始化能够使极深的模型收敛。相反，“Xavier”方法完全使学习停滞了，并且梯度在实验中逐渐减小。

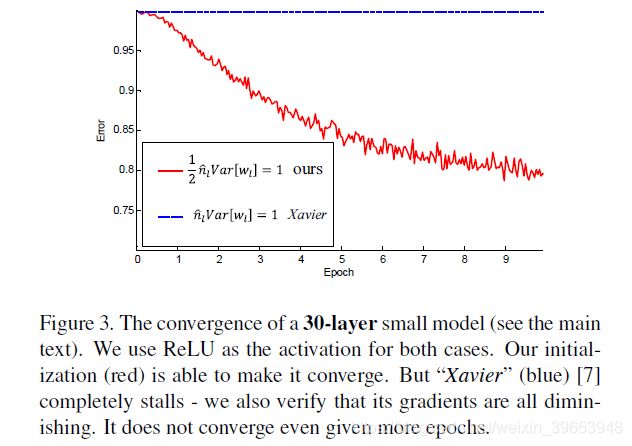
图3. 30层小模型的收敛性（请参见正文）。对于这两种情况，我们都使用ReLU作为激活。我们的初始化（红色）能够使其收敛。但是“Xavier”（蓝色）[7]完全停滞了-我们还验证了它的梯度都在减小。即使有更多的时期，它也不会收敛。

These studies demonstrate that we are ready to investigate extremely deep, rectified models by using a more principled initialization method. But in our current experiments on ImageNet, we have not observed the benefit from training extremely deep models. For example, the aforementioned 30-layer model has 38.56/16.59 top-1/top-5 error, which is clearly worse than the error of the 14-layer model in Table 2 (33.82/13.34). Accuracy saturation or degradation was also observed in the study of small models [10], VGG’s large models [25], and in speech recognition [34]. This is perhaps because the method of increasing depth is not appropriate, or the recognition task is not enough complex.

这些研究表明，我们已经准备好使用更原则的初始化方法来研究极深的，经过纠正的模型。但是，在我们目前在ImageNet上进行的实验中，我们还没有观察到训练极深模型的好处。例如，上述30层模型的top-1 / top-5误差为38.56 / 16.59，这显然比表2中的14层模型的误差（33.82 / 13.34）差。在小模型[10]，VGG的大模型[25]和语音识别[34]的研究中也观察到了准确性的饱和或下降。这可能是因为增加深度的方法不合适，或者识别任务不够复杂。

Though our attempts of extremely deep models have not shown benefits, ourinitializationmethodpavesafoundation for further study on increasing depth. We hope this will be helpful in other more complex tasks.

尽管我们对极深模型的尝试没有显示出任何好处，但是我们的初始化方法为进一步研究深度提供了基础。我们希望这将对其他更复杂的任务有所帮助。

2.3. Architectures

The above investigations provide guidelines of designing our architectures, introduced as follows.

以上调查提供了设计我们的网络结构的准则，介绍如下。

Our baseline is the 19-layer model (A) in Table 3. For a better comparison, we also list the VGG-19 model [25]. Our model A has the following modifications on VGG-19: (i) in the first layer, we use a filter size of 7×7 and a stride of 2; (ii) we move the other three conv layers on the two largest feature maps (224, 112) to the smaller feature maps (56, 28, 14). The time complexity (Table 3, last row) is roughly unchanged because the deeper layers have more filters; (iii) we use spatial pyramid pooling (SPP) [11] before the first fc layer. The pyramid has 4 levels - the numbers of bins are 7×7, 3×3, 2×2, and 1×1, for a total of 63 bins.

我们的基线是表3中的19层模型（A）。为了更好地进行比较，我们还列出了VGG-19模型[25]。我们的模型A对VGG-19进行了以下修改：（i）在第一层中，我们使用7×7的滤镜大小和2的步长； （ii）我们将两个最大特征图（224、112）上的其他三个转换层移到较小的特征图（56、28、14）。时间复杂度（表3，最后一行）大致保持不变，因为更深的层具有更多的滤波器。 （iii）我们在第一个fc层之前使用空间金字塔池（SPP）[11]。金字塔有4个级别的小块，数量分别为7×7、3×3、2×2和1×1，总共有63个小块。

It is worth noticing that we have no evidence that our model A is a better architecture than VGG-19, though our model A has better results than VGG-19’s result reported by [25]. In our earlier experiments with less scale augmentation, we observed that our model A and our reproduced VGG-19 (with SPP and our initialization) are comparable. The main purpose of using model A is for faster running speed. The actual running time of the conv layers on larger feature maps is slower than those on smaller feature maps, when their time complexity is the same. In our four-GPU implementation, our model A takes 2.6s per mini-batch (128), and our reproduced VGG-19 takes 3.0s, evaluated on four Nvidia K20 GPUs.

值得注意的是，尽管我们的模型A的结果要优于[25]报道的VGG-19的结果，但我们没有证据表明模型A的结构比VGG-19更好。在我们早期进行的规模较小的实验中，我们观察到模型A和复制的VGG-19（带有SPP和初始化）是可比的。使用模型A的主要目的是为了提高运行速度。当相同时间复杂度相同时，较大特征图上的卷积层的实际运行时间比较小特征图上的卷积层慢。在我们的四GPU实施中，模型A在每个微型批处理（128）中耗时2.6s，而我们复制的VGG-19在三个Nvidia K20 GPU上评估时耗时3.0s。

In Table 3, our model B is a deeper version of A. It has three extra conv layers. Our model C is a wider (with more filters) version of B. The width substantially increases the complexity, and its time complexity is about 2.3× of B (Table 3, last row). Training A/B on four K20 GPUs, or training C on eight K40 GPUs, takes about 3-4 weeks.

在表3中，我们的模型B是A的更深版本。它具有三个额外的转换层。我们的模型C是B的较宽版本（具有更多过滤器）。宽度大大增加了复杂度，其时间复杂度约为B的2.3倍（表3，最后一行）。在四个K20 GPU上进行A / B训练，或在八个K40 GPU上进行C训练，大约需要3-4周。

We choose to increase the model width instead of depth, because deeper models have only diminishing improvement or even degradation on accuracy. In recent experiments on small models [10], it has been found that aggressively increasing the depth leads to saturated or degraded accuracy. In the VGG paper [25], the 16-layer and 19-layer models perform comparably. In the speech recognition research of [34], the deep models degrade when using more than 8 hidden layers (all being fc). We conjecture that similar degradation may also happen on larger models for ImageNet. We have monitored the training procedures of some extremely deep models (with 3 to 9 layers added on B in Table 3), and found both training and testing error rates degraded in the first 20 epochs (but we did not run to the end due to limited time budget, so there is not yet solid evidence that these large and overly deep models will ultimately degrade). Because of the possible degradation, we choose not to further increase the depth of these large models.

我们选择增加模型宽度而不是深度，因为更深的模型只会减少改进甚至降低精度。在最近的小型模型实验中[10]，已经发现积极增加深度会导致饱和或降低精度。在VGG论文[25]中，16层和19层模型的性能相当。在[34]的语音识别研究中，当使用8个以上的隐藏层（全部为fc）时，深度模型会退化。我们推测，在较大的ImageNet模型上也可能发生类似的降级。我们已经监视了一些极深模型的训练过程（表3中的B上增加了3到9层），发现在前20个时期中训练和测试错误率均下降了（但由于时间预算有限，因此尚无确凿证据表明这些大型且过深的模型最终会降级）。由于可能的降级，我们选择不进一步增加这些大型模型的深度。

On the other hand, the recent research [5] on small datasets suggests that the accuracy should improve from the increased number of parameters in conv layers. This number depends on the depth and width. So we choose to increase the width of the conv layers to obtain a highercapacity model.

另一方面，最近关于小型数据集的研究[5]提出，随着conv层中参数数量的增加，精度应该有所提高。此数字取决于深度和宽度。因此，我们选择增加卷积层的宽度以获得更高的容量模型。

While all models in Table 3 are very large, we have not observed severe overfitting. We attribute this to the aggressive data augmentation used throughout the whole training procedure, as introduced below.

尽管表3中的所有模型都非常大，但我们并未发现严重的过拟合。我们将其归因于整个训练过程中使用的积极数据扩充，如下所述。

---

3. Implementation Details

Training

Our training algorithm mostly follows [16, 13, 2, 11, 25]. From a resized image whose shorter side is s, a 224×224 crop is randomly sampled, with the per-pixel mean subtracted. The scale s is randomly jittered in the range of [256,512], following [25]. One half of the random samples are flipped horizontally [16]. Random color altering [16] is also used.

我们的训练算法主要遵循[16、13、2、11、25]。从短边为s的调整大小的图像中，随机采样224×224作物，并减去每个像素的均值。在[25]之后，尺度s在[256,512]的范围内随机抖动，一半随机样本的水平翻转[16]，也使用随机颜色更改[16]。

Unlike [25] that applies scale jittering only during finetuning, we apply it from the beginning of training. Further, unlike [25] that initializes a deeper model using a shallower one, we directly train the very deep model using our initialization described in Sec. 2.2 (we use Eqn.(14)). Our endto-end training may help improve accuracy, because it may avoid poorer local optima.

与[25]仅在微调期间应用尺度抖动不同，我们从训练开始就应用它。此外，与[25]中使用较浅的模型初始化较深的模型不同，我们使用本节中介绍的初始化直接训练非常深的模型。 2.2（我们使用公式（14））。我们的端到端培训可以帮助提高准确性，因为它可以避免较差的局部最优性。

Other hyper-parameters that might be important are as follows. The weight decay is 0.0005, and momentum is 0.9. Dropout (50%) is used in the first two fc layers. The minibatch size is fixed as 128. The learning rate is 1e-2, 1e-3, and 1e-4, and is switched when the error plateaus. The total number of epochs is about 80 for each model.

其他可能很重要的超参数如下。权重衰减为0.0005，动量为0.9。前两个fc层使用Dropout（50％）。最小批量大小固定为128。学习率是1e-2、1e-3，和1e-4，并在错误达到稳定时切换。每个模型的epoch总数约为80。

Testing

We adopt the strategy of “multi-view testing on feature maps” used in the SPP-net paper [11]. We further improve this strategy using the dense sliding window method in [24, 25].

我们采用SPP网络论文[11]中使用的“特征图上的多视图测试”策略。我们在[24，25]中使用密集滑动窗口方法进一步改进了该策略。

We first apply the convolutional layers on the resized full image and obtain the last convolutional feature map. In the feature map, each 14×14 window is pooled using the SPP layer [11]. The fc layers are then applied on the pooled features to compute the scores. This is also done on the horizontally flipped images. The scores of all dense sliding windows are averaged [24, 25]. We further combine the results at multiple scales as in [11].

我们首先将卷积层应用到已调整大小的完整图像上，并获得最后的卷积特征图。在特征图中，每个14×14窗口都使用SPP层[11]池化。然后将fc层应用于池化特征以计算分数。在水平翻转的图像上也是如此。所有密集滑动窗口的分数均取平均值[24，25]。我们进一步将结果组合成多个尺度，如[11]。

Multi-GPU Implementation

We adopt a simple variant of Krizhevsky’s method [15] for parallel training on multiple GPUs. We adopt “data parallelism” [15] on the conv layers. The GPUs are synchronized before the first fc layer. Then the forward/backward propagations of the fc layers are performed on a single GPU this means that we do not parallelize the computation of the fc layers. The time cost of the fc layers is low, so it is not necessary to parallelize them. This leads to a simpler implementation than the “model parallelism” in [15]. Besides, model parallelism introduces some overhead due to the communication of filter responses, and is not faster than computing the fc layers on just a single GPU.

我们采用Krizhevsky方法的简单变体[15]在多个GPU上进行并行训练。我们在conv层采用了“数据并行性” [15]。在第一个fc层之前同步GPU。然后，在单个GPU上执行fc层的向前/向后传播，这意味着我们不并行化fc层的计算。 fc层的时间成本很低，因此不必并行化它们。这比[15]中的“模型并行性”导致更简单的实现。此外，模型并行性由于过滤器响应的传递而引入了一些开销，并且不比仅在单个GPU上计算fc层快。

We implement the above algorithm on our modification of the Caffe library [14]. We do not increase the mini-batch size (128) because the accuracy may be decreased [15]. For the large models in this paper, we have observed a 3.8x speedup using 4 GPUs, and a 6.0x speedup using 8 GPUs.

我们在对Caffe库的修改中实现了上述算法[14]。我们不会增加小批量的大小（128），因为精度可能会降低[15]。对于本文中的大型模型，我们观察到使用4个GPU的速度提高了3.8倍，使用8个GPU的速度提高了6.0倍。

---

4. Experiments on ImageNet

We perform the experiments on the 1000-class ImageNet 2012 dataset [22] which contains about 1.2 million training images, 50,000 validation images, and 100,000 test images (with no published labels). The results are measured by top1/top-5 error rates [22]. We only use the provided data for training. All results are evaluated on the validation set, except for the final results in Table 7, which are evaluated on the test set. The top-5 error rate is the metric officially used to rank the methods in the classification challenge [22].

我们对1000级ImageNet 2012数据集[22]进行了实验，该数据集包含约120万个训练图像，50,000个验证图像和100,000个测试图像（没有发布的标签）。结果通过top1 / top-5错误率测量[22]。我们仅使用提供的数据进行培训。除表7中的最终结果（在测试集上评估）外，所有结果均在验证集上评估。前五位错误率是在分类挑战中正式用于对方法进行排名的度量标准[22]。

Comparisons between ReLU and PReLU
In Table 4, we compare ReLU and PReLU on the large model A. We use the channel-wise version of PReLU. For fair comparisons, both ReLU/PReLU models are trained using the same total number of epochs, and the learning rates are also switched after running the same number of epochs.

在表4中，我们在大型模型A上比较了ReLU和PReLU。我们使用PReLU的通道方式。为了公平地进行比较，两个ReLU / PReLU模型都使用相同的时期总数进行训练，并且在运行相同的时期之后也可以切换学习率。

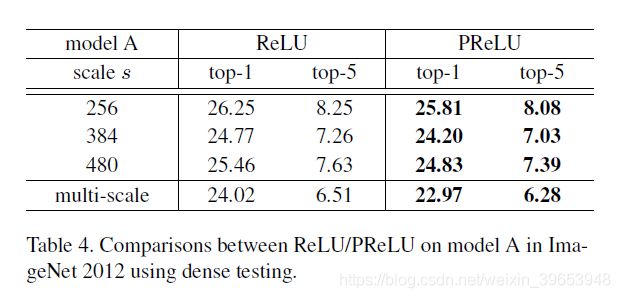
Table 4 shows the results at three scales and the multiscale combination. The best single scale is 384, possibly because it is in the middle of the jittering range [256,512]. For the multi-scale combination, PReLU reduces the top1 error by 1.05% and the top-5 error by 0.23% compared with ReLU. The results in Table 2 and Table 4 consistently show that PReLU improves both small and large models. This improvement is obtained with almost no computational cost.

表4显示了三个等级和多等级组合的结果。最佳的单刻度是384，可能是因为它在抖动范围的中间[256,512]。对于多尺度组合，与ReLU相比，PReLU将top1误差降低了1.05％，将top-5误差降低了0.23％。表2和表4中的结果始终表明，PReLU可以改善小型和大型模型。几乎没有计算成本就能获得这种改进。

Comparisons of Single-model Results

Next we compare single-model results. We first show 10view testing results [16] in Table 5. Here, each view is a 224-crop. The 10-view results of VGG-16 are based on our testing using the publicly released model [25] as it is not reported in [25]. Our best 10-view result is 7.38% (Table 5). Our other models also outperform the existing results.

接下来，我们比较单模型结果。我们首先在表5中显示10view测试结果[16]。这里，每个视图都是一个224个作物。 VGG-16的10个视图结果基于我们使用公开发布的模型[25]进行的测试，因为在[25]中未进行报告。我们最好的10个视图结果是7.38％（表5）。我们的其他模型也优于现有结果。

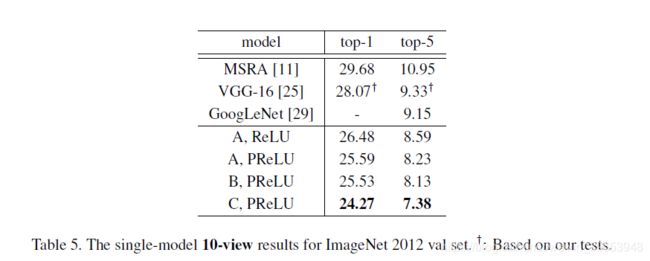
Table 6 shows the comparisons of single-model results, which are all obtained using multi-scale and multi-view (or dense) test. Our results are denoted as MSRA. Our baseline model (A+ReLU, 6.51%) is already substantially better than the best existing single-model result of 7.1% reported for VGG-19 in the latest update of [25] (arXiv v5). We believe that this gain is mainly due to our end-to-end training, without the need of pre-training shallow models.

表6显示了单模型结果的比较，这些结果都是使用多尺度和多视图（或密集）测试获得的。我们的结果表示为MSRA。我们的基线模型（A + ReLU，6.51％）已经大大优于最新[25]（arXiv v5）中针对VGG-19报告的最佳现有单模型结果7.1％。我们相信，这种收益主要是由于我们进行了端到端的培训，而无需预先训练浅层模型。

Moreover, our best single model (C, PReLU) has 5.71% top-5 error. This result is even better than all previous multi-model results (Table 7). Comparing A+PReLU with B+PReLU, we see that the 19-layer model and the 22-layer model perform comparably. On the other hand, increasing the width (C vs. B, Table 6) can still improve accuracy. This indicates that when the models are deep enough, the width becomes an essential factor for accuracy.

此外，我们最好的单一模型（C，PReLU）的top-5误差为5.71％。该结果甚至比以前所有的多模型结果都要好（表7）。将A + PReLU与B + PReLU进行比较，我们看到19层模型和22层模型具有可比的性能。另一方面，增加宽度（C vs. B，表6）仍可以提高精度。这表明，当模型足够深时，宽度成为精度的重要因素。

Comparisons of Multi-model Results

We combine six models including those in Table 6. For the time being we have trained only one model with architecture C. The other models have accuracy inferior to C by considerable margins. We conjecture that we can obtain better results by using fewer stronger models.

我们结合了包括表6中的模型在内的六个模型。目前，我们仅训练了一个具有C架构的模型。其他模型的准确性比C差很多。我们推测可以通过使用更少的更强模型来获得更好的结果。

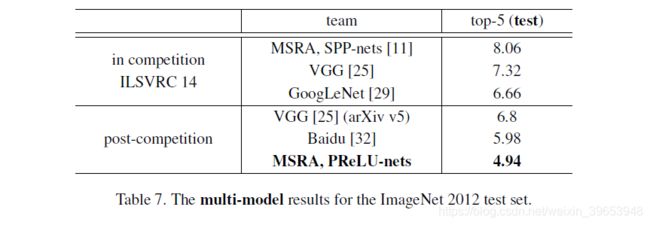
The multi-model results are in Table 7. Our result is 4.94% top-5 error on the test set. This number is evaluated by the ILSVRC server, because the labels of the test set are not published. Our result is 1.7% better than the ILSVRC 2014 winner (GoogLeNet, 6.66% [29]), which represents a ∼26% relative improvement. This is also a ∼17% relative improvement over the latest result (Baidu, 5.98% [32]).

多模型结果在表7中。我们的结果是测试集上4.95％的top-5错误。该数字由ILSVRC服务器评估，因为未发布测试集的标签。我们的结果比2014年ILSVRC冠军（GoogLeNet，6.66％[29]）高1.7％，相对而言提高了约26％。这也比最新结果（百度，5.98％[32]）高出约17％。

Analysis of Results

Figure 4 shows some example validation images successfully classified by our method. Besides the correctly predicted labels, we also pay attention to the other four predictions in the top-5 results. Some of these four labels are other objects in the multi-object images, e.g., the “horse-cart” image (Figure 4, row 1, col 1) contains a “mini-bus” and it is also recognized by the algorithm. Some of these four labels are due to the uncertainty among similar classes, e.g., the “coucal” image (Figure 4, row 2, col 1) has predicted labels of other bird species.

图4显示了一些通过我们的方法成功分类的示例验证图像。除了正确预测的标签外，我们还应注意前5个结果中的其他四个预测。这四个标签中的某些标签是多对象图像中的其他对象，例如，“马车”图像（图4，第1行，第1行）包含“horse-cart”，并且算法也可以识别。这四个标签中的某些标签是由于相似类别之间的不确定性所致，例如，“coucou”图像（图4，第2行，第1栏）已预测了其他鸟类的标签。

图4.通过我们的方法成功分类的示例验证图像。对于每幅图像，均列出了通过我们的方法预测的真实标签和前5个标签。

Figure 6 shows the per-class top-5 error of our result (average of 4.94%) on the test set, displayed in ascending order. Our result has zero top-5 error in 113 classes the images in these classes are all correctly classified. The three classes with the highest top-5 error are “letter opener” (49%), “spotlight” (38%), and “restaurant” (36%). The error is due to the existence of multiple objects, small objects, or large intra-class variance. Figure 5 shows some example images misclassified by our method in these three classes. Some of the predicted labels still make some sense.

图6显示了我们的测试集结果的每类top-5错误（平均值为4.94％），以升序显示。我们的结果在113个类别中的top-5错误为零，这些类别中的图像均被正确分类。top-5错误最高的三个类别是“letter opener”（49％），“spotlight”（38％）和“restaurant”（36％）。该错误是由于存在多个对象，较小的对象或较大的组内方差。图5显示了在这三个类中被我们的方法误分类的一些示例图像。一些预测标签仍然有意义。

图5.在我们的方法中，在top-5测试错误最高的三个类别中，验证图像示例未正确分类。顶部：“开信刀”（49％的前5位测试错误）。中：“聚光灯”（38％）。下：“餐厅”（36％）。对于每幅图像，均列出了通过我们的方法预测的真实标签和前5个标签。

In Figure 7, we show the per-class difference of top-5 error rates between our result (average of 4.94%) and our team’s in-competition result in ILSVRC 2014 (average of 8.06%). The error rates are reduced in 824 classes, unchanged in 127 classes, and increased in 49 classes.

在图7中，我们显示了我们的结果（平均4.94％）与我们团队在ILSVRC 2014中的竞赛中结果（平均8.06％）之间的前5个错误率的按类别差异。错误率降低了824个类，错误率降低了127个类，错误率提高了49个类。

Comparisons with Human Performance from [22]

Russakovsky et al. [22] recently reported that human performance yields a 5.1% top-5 error on the ImageNet dataset. This number is achieved by a human annotator who is well trained on the validation images to be better aware of the existence of relevant classes. When annotating the test images, the human annotator is given a special interface, where each class title is accompanied by a row of 13 example training images. The reported human performance is estimated on a random subset of 1500 test images.

Russakovsky等[22]最近报告说，人类在ImageNet数据集上产生了5.1％的top-5错误。这个数字是由人工注释者实现的，该注释者在验证图像上训练有素，可以更好地了解相关类的存在。在对测试图像进​​行注释时，将为人类注释者提供一个特殊的界面，其中每个类标题均附带一行13个样本训练图像。报告的人类表现是根据1500张测试图像的随机子集估算的。

Our result (4.94%) exceeds the reported human-level performance. To our knowledge, our result is the first published instance of surpassing humans on this visual recognition challenge. The analysis in [22] reveals that the two major types of human errors come from fine-grained recognition and class unawareness. The investigation in [22] suggests that algorithms can do a better job on fine-grained recognition (e.g., 120 species of dogs in the dataset). The second row of Figure 4 shows some example fine-grained objects successfully recognized by our method - “coucal”, “komondor”, and “yellow lady’s slipper”. While humans can easily recognize these objects as a bird, a dog, and a flower, it is nontrivial for most humans to tell their species. On the negative side, our algorithm still makes mistakes in cases that are not difficult for humans, especially for those requiring context understanding or high-level knowledge (e.g., the “spotlight” images in Figure 5).

我们的结果（4.94％）超出了报告的人员平均水平。据我们所知，我们的结果是在视觉识别挑战方面超越人类的首次公开实例。文献[22]中的分析表明，人为错误的两种主要类型来自细粒度的识别和对类的无意识。 [22]中的研究表明，算法在细粒度识别（例如，数据集中的120种狗）方面可以做得更好。图4的第二行显示了一些通过我们的方法成功识别的样本中细粒度对象：“ coucal”，“ komondor”和“ yellow lady’s slipper”。尽管人类可以轻松地将这些物体识别为鸟，狗和花，但对于大多数人类来说，分辨它们的种类并不容易。不利的一面是，在对人类来说并不困难的情况下，尤其是对于那些需要上下文理解或高水平知识的情况（例如，图5中的“聚光灯”图像），我们的算法仍然会犯错误。

While our algorithm produces a superior result on this particular dataset, this does not indicate that machine vision outperforms human vision on object recognition in general. On recognizing elementary object categories (i.e., common objects or concepts in daily lives) such as the Pascal VOC task [6], machines still have obvious errors in cases that are trivial for humans. Nevertheless, we believe that our results show the tremendous potential of machine algorithms to match human-level performance on visual recognition.

虽然我们的算法在该特定数据集上产生了优异的结果，但这并不表示机器视觉在对象识别方面总体上胜过人类视觉。在识别诸如Pascal VOC任务之类的基本对象类别（即日常生活中的常见对象或概念）时，在对于人类来说微不足道的情况下，机器仍然存在明显的错误。尽管如此，我们相信我们的结果显示了机器算法在视觉识别上与人类水平的表现相匹配的巨大潜力。