共轭梯度(CG)算法
共轭梯度(CG)方法
简单介绍
共轭梯度方法也是一种迭代方法,不同于Jacobi,Gauss-Seidel和SOR方法,理论上只要n步就能找到真解,实际计算中,考虑到舍入误差,一般迭代3n到5n步,每步的运算量相当与矩阵乘向量的运算量,对稀疏矩阵特别有效。
共轭梯度方法对于求解大型稀疏矩阵是很棒的方法,但是这个方法看起来总不是太靠谱。这个方法也不是越迭代精度越高,有时候可能迭代多了,反而出错,对迭代终止条件的选择,要求还是很高的。
共轭梯度法收敛的快慢依赖于系数矩阵的谱分布情况,当特征值比较集中,系数矩阵的条件数很小,共轭梯度方法收敛得就快。“超线性收敛性”告诉我们,实际当中,我们往往需要更少的步数就能得到所需的精度的解。
基本思想和原理核心
考虑线性对称正定方程组: A x = b Ax = b Ax=b 可以转化为求解二次泛函 ϕ ( x ) = 1 2 x T A x − b T x 。 \phi(x) = \frac{1}{2} x^TAx-b^Tx。 ϕ(x)=21xTAx−bTx。
的最小值问题,直接可以验证 ϕ ′ ( x ) = A x − b \phi'(x)=Ax-b ϕ′(x)=Ax−b。
当然,选择其他的二次泛函也能满足这个条件导数等于这个的条件了,那是另外的一些方法了,这里不提。
比如说这里取 A = d i a g ( 2 , 2 ) , b = [ 2 , 2 ] T A = diag(2,2),b=[2,2]^T A=diag(2,2),b=[2,2]T,那么就有 1 2 x T A x − b T x = x 1 2 + x 2 2 − 2 x 1 − 2 x 2 = ( x 1 − 1 ) 2 + ( x 2 − 1 ) 2 − 2 \frac{1}{2}x^TAx-bTx = x_1^2+x_2^2-2x_1-2x_2=(x_1-1)^2+(x_2-1)^2-2 21xTAx−bTx=x12+x22−2x1−2x2=(x1−1)2+(x2−1)2−2
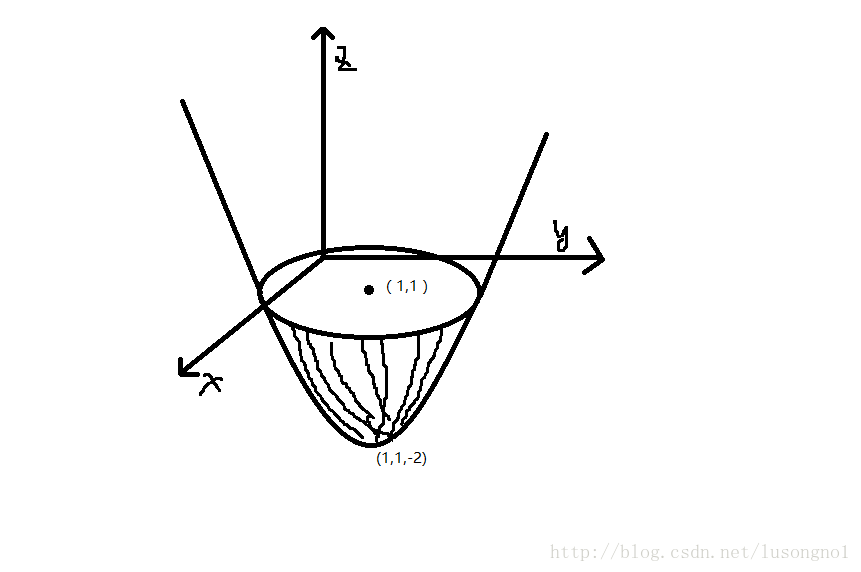
这里可以看出它是一个尖朝下,经过源点的椭圆抛物面(当然,这个例子中椭圆是圆),且在 ( 1 , 1 ) (1,1) (1,1)点达到最小值-2。如下图所示(手绘的,比较丑,不过我已经很努力了):
在介绍共轭梯度法前,我们得先说一个这样一个二次泛函的性质,用大白话来说,就是这样:
-
用一根xy平面上的直线穿过二次曲面在xy平面上的值形成的椭圆,那么这个直线上的二次泛函的值在直线被椭圆截出的线段的中点处取到最小。且这个最小值是唯一的,如图。

-
最小值的梯度方向垂直于上面提到的那根直线。
-
最小值点位于位于这根直线的共轭超平面上(一维),不知道什么是共轭超平面,没有涉及到公式推导计算,这里可先不用管,只要知道它是由这根直线的法平面和 A A A以及真解有关的一个平面即可。
这个其实很好理解,对于二次泛函形成的函数图像,我们沿着每个方向用一个平行于z轴的平面去切它,得到的是一个抛物面,放到坐标平面上,就是一根抛物线,抛物线的最小值点当然在中点处取到。注意,这里的负梯度方向,就是沿最速下降方向,它不一定能经过椭圆的圆心。
以上是以最简单的二维的情况来说明这个问题,更高维的情况也如是。比如说三维的情况,我们可以想象有一个西瓜,它的内部每一点处有某一种性质,比如说甜度(或密度等等),假设它在正中心处甜度最高,最外面是瓜皮最不甜,依次往里甜度是呈抛物增长的。那么,我们拿一把刀,给它切一刀(不一定对半),会形成一个切面,那么这个切面是个椭圆,且在椭圆的正中间是最甜的(极值点),拿一根牙签,从这个最甜的点垂直切面往里面一戳,这个方向就是这一点负梯度方向。当然,牙签够长,你也不一定能正好西瓜正中心。因此才有了从最速下降法到共轭梯度法的改进。
有了以上的思想,我们很容易就能推导出共轭梯度法的算法过程,不想摆公式,还是以切西瓜为例:
-
首先我们拿一根足够长的牙签沿着西瓜任意位置将它穿透,那么前面的性质告诉我们没在西瓜中的牙签的中点就是这根牙签上的最值点。(这其实就是最速下降方法的步骤,最速下降法往往是沿着一个方向取到最小,步长以此来决定,接着换一个方向,同样一个过程……)
-
接着找到最值点(牙签中点)的梯度方向,最速下降法就是以梯度方向接着找最小值点,但我们现在不这么做。梯度方向和原来的牙签的方向形成了一个面,我们试图在这个面里面找一个更好的方向。前面的性质告诉我们,这个切面的中点是这个面的最小值点,那么我就应该以牙签中点和这个切面的连线作为方向是最理想的。
-
问题是这个切面的中点不好找,好在前面的性质告诉我们,这个切面的中点的梯度方向是垂直于这个切面的,把提到的这几个条件联立起来,其实很快就能找到牙签中点和切面中点的连线方向,以及我们所需要的步长。
把以上的过程用公式摆开,就得到了共轭梯度法算法过程,如下算法框图所示:

当然,共轭梯度算法并不是很快,后来人们提出了很多方法去加快这个速度,比如说各种预优方法等等,都是后话,这里不提。
程序代码和结果
C代码
#include
#include
#include
#include
#define N 5
#define epsilon 0.005
void main()
{
void matrixTimesVec(double A[N][N], double b[N], double Ab[N]);
double scalarProduct(double vec1[], double vec2[]);
void vecPlus(double vec1[], double vec2[], double vec[]);
void numPlusVec(double num, double vec0[], double vec[]);
int i, j;
static double A[N][N] = { 0 };
static double b[N] = { 1, 1, 1, 1, 1 };
static double x0[N] = { 1, 1, 1, 1, 1 };
double x[N], r[N], p[N], w[N], alpha, rho00, rho0, rho1, beta;
//生成一个大规模稀疏矩阵A,这里以三对角为例。
for (i = 1; i < N - 1; i++)
{
A[i][i - 1] = 2;
A[i][i] = 3;
A[i][i + 1] = 1;
}
A[0][0] = 3; A[0][1] = 1;
A[N - 1][N - 2] = 2; A[N - 1][N - 1] = 3;
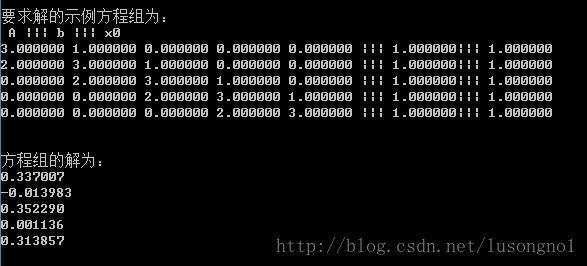
printf("\n要求解的示例方程组为:\n A ||| b ||| x0\n");
for (i = 0; i < N; i++)
{
for (j = 0; j < N; j++)
{
printf("%f ", A[i][j]);
}
printf("||| %f||| %f\n", b[i], x0[i]);
}
//init
memcpy(x, x0, N*sizeof(double));
double Ax0[N];
matrixTimesVec(A, x0, Ax0);
numPlusVec(-1.0, Ax0, Ax0);
vecPlus(b, Ax0, r);
rho0 = scalarProduct(r, r);
rho00 = rho0;
memcpy(p, r, N*sizeof(double));
do
{
matrixTimesVec(A, p, w);
alpha = rho0 / (scalarProduct(p, w));
double temp[N];
numPlusVec(alpha, p, temp);
double x_temp[N];
vecPlus(x, temp, x_temp);
memcpy(x, x_temp, N*sizeof(double));
numPlusVec(-alpha, w, temp);
double r_temp[N];
vecPlus(r, temp, r_temp);
memcpy(r, r_temp, N*sizeof(double));
rho1 = scalarProduct(r, r);
beta = rho1 / rho0;
numPlusVec(beta, p, temp);
vecPlus(r, temp, p);
rho0 = rho1;
} while (rho1 > epsilon);
printf("\n\n");
printf("方程组的解为:\n");
for (i = 0; i < N; i++)
printf("%f\n", x[i]);
getchar();
}
void matrixTimesVec(double A[N][N], double b[N], double Ab[N])
{
int i, j;
for (i = 0; i < N; i++)
{
Ab[i] = 0.0;
for (j = 0; j < N; j++)
{
Ab[i] = Ab[i] + A[i][j] * b[j];
}
}
}
double scalarProduct(double vec1[], double vec2[])
{
double s = 0;
int i;
for (i = 0; i < N; i++)
{
s = s + vec1[i] * vec2[i];
}
return s;
}
void vecPlus(double vec1[], double vec2[], double vec[])
{
int i;
for (i = 0; i < N; i++)
{
vec[i] = vec1[i] + vec2[i];
}
}
void numPlusVec(double num, double vec0[], double vec[])
{
int i;
for (i = 0; i < N; i++)
vec[i] = num*vec0[i];
}
MATLAB代码
clc
clear
%% 共轭梯度算法并不是迭代的次数越多越精确,所以要合理地设置迭代终止的的条件。
epsilon = 0.005;
N = 5;
A = zeros(N);
for i=2:N-1
A(i,i-1)=2;
A(i,i) = 3;
A(i,i+1) =1;
end
A(1,1)=3;
A(1,2) = 1;
A(N,N-1) = 2;
A(N,N) = 3;
b = ones(N,1);
x0 = b;
%% 初始化
x = x0;
r = b - A*x0;
rho0 = conj(r')*r;
rho00 = rho0;
p=r;
while(rho0>0.005)
w= A*p;
alpha = rho0/(conj(p')*w);
x = x+alpha*p;
r = r- alpha*w;
rho1 = conj(r')*r;
beta = rho1/rho0;
p = r + beta*p;
rho0 = rho1;
x
end
A\b
x