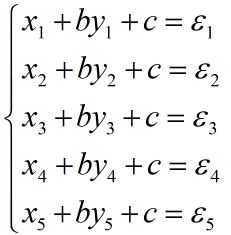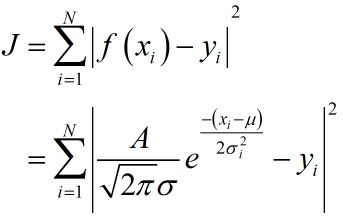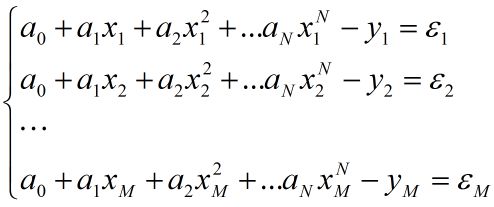作者:桂。
时间:2017-03-11 06:45:46
链接:http://www.cnblogs.com/xingshansi/p/6533840.html
声明:欢迎转载,不过记得注明出处哦~
前言
数据拟合中,最常用的两个就是曲线拟合(curve fitting)与分布拟合(distribution fitting),不求面面俱到,只希望串出一个思路,篇目如下:
1)曲线拟合、分布拟合,区别与联系;
2)生成给定分布随机数;
3)曲线拟合:
单个曲线拟合:高斯曲线、拉普拉斯/瑞利/对数正态 曲线
混合曲线:多直线的EM拟合
4)分布拟合;
单分布拟合:正态/拉普拉斯/对数高斯/瑞利 分布
混合分布拟合:GMM(混合高斯)、LMM(混合拉普拉斯)
内容为自己的学习整理,其中借鉴他人的地方,最后一并给出链接。
一、常用分布
本文仅介绍几种自己日常使用的分布,并以Normal distribution为例交代推导过程及代码实现,其他可类推。
关于以下几种分布随机数的产生方法,戳这里会略有一二,并附有对应的代码实现。
以下四种分布的拟合推导、代码实现,参考这里。
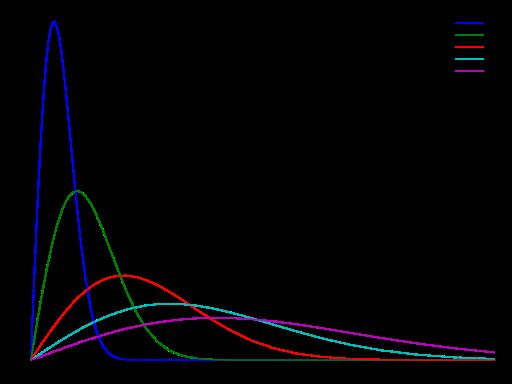
A-瑞利分布(Rayleigh distribution)
表达式:
$f(x) = \frac{x}{{{\sigma ^2}}}{e^{ - \frac{{{x^2}}}{{2{\sigma ^2}}}}}$
其中$\sigma > 0$,
B-正态分布(Normal distribution)
表达式:
$f(x) = \frac{1}{{\sqrt {2\pi } \sigma }}{e^{ - \frac{{{{(x - \mu )}^2}}}{{2{\sigma ^2}}}}}$
C-对数正态分布(Log-Normal distribution)
表达式:
$f(x) = \frac{1}{{x\sqrt {2\pi } \sigma }}{e^{ - \frac{{{{(\ln x - \mu )}^2}}}{{2{\sigma ^2}}}}}$
D-拉普拉斯分布(Laplace distribution)
$f(x) = \frac{1}{{2b}}{e^{ - \frac{{\left| {x - \mu } \right|}}{b}}}$
具体细节,可点击如下链接:
- Rayleigh distribution:wikipedia.
- Normal distribution:wikipedia.
- Log-normal distribution:wikipedia.
- Laplace distribution:wikipedia.
二、曲线拟合
A-问题描述
根据随机过程一文的分析可知,曲线拟合解决的问题是:确定函数+随机噪声,拟合出确定函数的表达式。
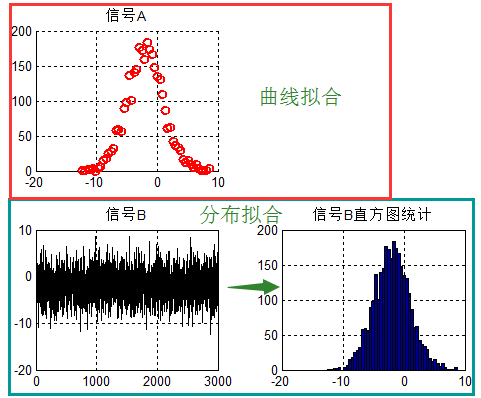
给出示意图:
曲线分布即针对信号A进行拟合。
B-原理推导
1-闲话小叙
此处用到最小二乘拟合的方法,关于该方法此处简单提一下。
假设有测量点{$x_1,y_1$}和{$x_2,y_2$},且x、y之间有线性关系,尽管测量存在误差,我们仍然可以近似得出:
$\left\{ \begin{array}{l}
{x_1} + b{y_1} + c = 0\\
{x_2} + b{y_2} + c = 0
\end{array} \right.$
这是二元二次方程,容易求解。现在问题是,测量点远大于2个,此处以5个为例:
如果理想情况,我们任取两个方程,即可求解。现实情况是:测量不可避免地带来误差。每组的解都不同,如何解决求值问题?天文学家梅耶给的办法是:将方程分两组,分别叠加,这样就转化成了两个方程,进而求解,拉普拉斯也给出了类似的方法。
但都没有跳出直接解方程的思路,是勒让德重新认识了该问题:从全局误差的角度,将线性方程组变成了正则方差组。剑锋一转,确定性问题立刻变为随机过程的统计问题。
表达式重新定义:(其中${{\varepsilon _i}}$为对应的误差)
于是上面的问题便有了新的准则函数:
针对J求解即可,常用的有矩阵求逆、准则函数求偏导的方式。
更多的细节,可以参考:《数理统计学简史》第四章,陈希孺。
2-回归正题
以高斯曲线拟合为例,利用最小二乘准则:
分别对准则函数求偏导,得出参数估计。
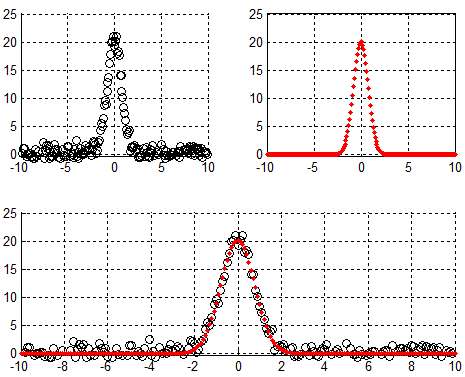
对应拟合结果图:
本文主要分析拟合原理,对应的推导与代码,限于篇幅,拟在另一篇文章中给出。
实际上,如果仅仅是应用,对于高斯分布、拉普拉斯分布等对称分布,可以利用:
- 统计均值 = 分布的均值;
- 统计数值的峰值 = 分布的峰值;
这样一来,分布的拟合基本就剩一个参数,直接求解更加方便。
三、分布拟合
A-问题描述
分布拟合解决的问题是:随机过程,拟合处随机过程的统计特性。
分布拟合,即针对信号B进行拟合。注意:是信号B,而不是信号B的直方图(不过二者可以转化,另一篇文章将会给出二者的转化关系)。
B-原理推导
统计分布的拟合,此处给出的例子主要借助最大似然估计的方法。
1-闲话小叙
我们假设某随机过程具有遍历性(什么是遍历性?就像一周有7天,我们每天都经历,具体可参考另一篇博文),以下分析基于遍历性假设。
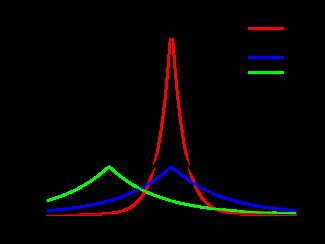
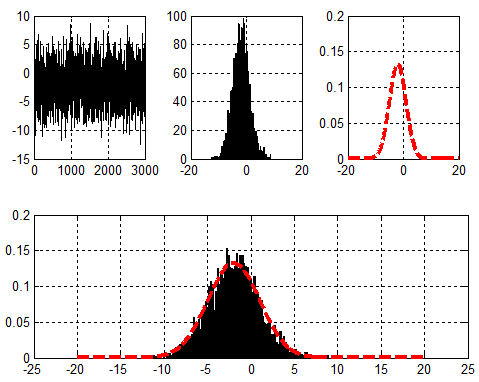
先来看一张图,对随机信号进行统计拟合:
最大似然估计(Maximum Likelihood Estimation,MLE),(对于概率密度估计,MLE只是方法之一,其他有基于histogram估计,kernel density estimation等等,具体可以google,关键词:histogram/probability density estimation/KDE等)
补充:有朋友问到直方图如何与概率分布绘制在同一张图里,这涉及到:直方图归一化。
2-回归正题
以正态分布为例,假设各观察变量服从独立同分布的假设,概率密度函数记为$f(x)$,对观测数据{$x_1, x_2, x_3,... x_N$},得到联合概率密度:
$L = f({x_1})f({x_2})...f({x_N})$
正态分布中,需要估计的参数有{$\mu ,\delta $};推而广之,假设概率密度函数$f(x)$的参数集合记为$\theta $,概率密度函数$f(x)$标准写法应为$f(x;\theta)$,联合概率密度函数:
$L\left( \theta \right) = f({x_1};\theta )f({x_2};\theta )...f({x_N};\theta )$
由于高斯分布中含有指数,通常对$L\left( \theta \right)$进行取对数:
$J\left( \theta \right) = \ln L\left( \theta \right) = \ln f({x_1};\theta ) + \ln f({x_2};\theta ) + ... + \ln f({x_N};\theta )$
具体原理推导及代码实现,参考另一篇文章。
四、最大似然与最小二乘
最大似然与最小二乘存在着内在的联系,此处论述纯粹是一家之言,严谨与否不予保证。(更多信息,可以参考:最小二乘、Ridge回归、Lasso回归与概率分布的关系)
给出数学模型(以多项式拟合为例,N次拟合,共M组样本点):
最小二乘准则函数:
最大似然准则:
假设误差均服从(0,$\delta^2$)的正态分布,则有似然函数:
求对数之后,最大似然准则函数等价于:
二者等价。
五、曲线拟合与分布拟合
A-工具箱使用
MATLAB有cftool、dfittool两个指令,分别对应曲线拟合与分布拟合,可调用。
B-二者转化关系
曲线—>分布:可以借助给定曲线,生成满足指定分布的随机数,从而曲线拟合转化为分布拟合问题;
分布—>曲线:参数估计法:单个模型拟合、混合模型拟合都属于此类,利用分布得到概率特性; 非参法:经典的有Parzen、Kn近邻等估计方式,本质上都是利用统计信息,或者说借助直方图,不再展开叙述。