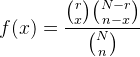离散型概率分布

目录

1.1 随机变量

1.2 离散型概率分布

1.3 数学期望与方差、标准差

1.3.1 数学期望

1.3.2 方差

1.3.3 标准差

1.3.4 线性变换的通用公式

1.3.5 独立观测值

1.4 二项概率分布（binomial probability distribution）

1.5 泊松概率分布（poisson probability distribution）

1.6 超几何概率分布（hypergeometric probability distribution）

1.7 几何分布（Geometric distribution）

---

1.1 随机变量

随机变量（random variable）是对一个试验结果的数值描述，是一个可以等于一系列数值的变量。

而这一系列数值的每一个值都与一个特定概率相关联。

▪离散型随机变量：可以取有限多个数值或无限可数多个数值的随机变量

▪连续型随机变量：可以在某一区间或多个区间内任意取值的随机变量

1.2 离散型概率分布

随机变量的概率分布（probability distribution）是描述随机变量取不同值的概率。

对于离散型随机变量x，概率函数给出随机变量取每一种值的概率，记f(x)

离散型概率函数的基本条件

（1）        对于任意随机变量的取值，函数值都是大于等于0

（2）    随机变量的所有取值对应的概率之和为1

1.3 数学期望与方差、标准差

1.3.1 数学期望

随机变量的数学期望或均值是对随机变量中心位置的一种度量。

离散型随机变量的数学期望：

数学期望和均值有点儿像，甚至计算方法也相似，但数学期望描述的是概率分布。

1.3.2 方差

方差用来描述随机变量取值的变异性

离散型随机变量的方差：

方差公式的关键是 离差（x-u），它度量了随机变量某一特定值与数学期望或均值u的距离。

1.3.3 标准差

概率分布的标准差，度量了数据与数据中心的数学期望的距离。

标准差取方差的平方根。

1.3.4 线性变换的通用公式

若随机变量为X：

   -- 期望乘以a，然后加b

   -- 取a的平方，乘以X的方差，忽略b

1.3.5 独立观测值

X的独立观测值与X不同，每个观测值都具有相同的概率分布，但结果各不一样。

比如，抛硬币，连续抛几次，每一次抛硬币的结果称为一个观测值，每一个观测值具有相同的期望和方差，但观测值之间没有关系，互不影响。

如果X1,X2,...,Xn是随机变量X的独立观测值，则：

如果X和Y是独立随机变量，则：

如果X和Y是独立随机变量，X和Y的线性变化的期望和方差用下列各式进行计算：

1.4 二项概率分布（binomial probability distribution）

二项试验（binomial experiment）具有以下四个性质：

（1）试验由一系列相同的n个试验组成

（2）每次试验由两种可能的结果，即试验结果由两个值构成，其中每个值与一个随机变量对应。我们把其中一个称为成功，另一个称为失败

（3）每次试验成功的概率都是相同的，用p来表示；失败的概率也是相同，用 1 – p表示

（4）试验是相互独立的

二项概率函数

说明：n代表试验的次数；x代表成功的次数；p代表一次试验中成功的概率；f(x)代表n次试验中有x次成功的概率；

      --- 代表了n次试验中有x次成功试验结果的个数。

二项分布的数学期望和方差

二项分布的众数

一个概率分布的众数就是具有最高概率的数值。

如果p=0.5且n为偶数，则众数为np；

如果p=0.5且n为奇数，则该概率分布有两个众数，即位于np左右两侧的两个数值。

二项分布形状特点:

根据n和p的不同数值，二项分布的形状会发生变化。p越接近0.5，图形越堆成。一般情况下，当p小于0.5时，图形向右偏斜；当p大于0.5时，图形向左偏斜。

什么时候使用二项分布？

进行次数固定的独立试验时可使用二项分布，这时，每一次试验都存在成功或失败的可能，而你感兴趣的是成功或失败的次数。

1.5 泊松概率分布（poisson probability distribution）

泊松分布主要用于估计某事件在特定时间段或空间中发生的次数。

如果事件出现的次数满足以下两个性质，则随机变量服从泊松概率分布：

（1）在任意两个相等长度的区间上，事件发生的概率相等

（2）事件在任一区间上是否发生，于事件在其他区间上是否发生是独立的

泊松概率函数

f(x)代表事件在一个区间上发生x次的概率；u代表事件在一个区间上发生次数的数学期望或均值；e=2.718 28

什么时候使用泊松分布？

在遇到独立事件时（例如机器在给定区间内发生故障），若已知u（即给定区间内的事件平均发生次数（发生率）），而你很感兴趣的是一个特定区间内的发生次数，我们就可以根据给出的参数u得到泊松概率分布函数。

那么u必须是整数吗？

完全不是这样。期望或均值u可以是任何非负数，但不能是负数。它代表了在一定区间内事件发生的平均次数，如果是负数就没有意义了。

泊松分布的数学期望与方差

E(x) = u

Var(x) = u
所以泊松分布参数本身，就是其数学期望和方差。

泊松分布的众数

如果u是一个整数，则有两个众数，u和u-1；如u不是整数，众数为u。

泊松分布形状特点:

泊松分布的形状随着均值u的数值发生变化。u小，则分布向右倾斜，随着u的变大，分布逐渐变得对称。

为什么泊松分布均值不适用λ表示？

因为泊松分布的均值、期望、方差都相等，一般会有λ表示，可以确保公正。

本文为了和上下文统一，避免太多符号出现，均值统一用u表示。

泊松分布和二项分布的关系？

如果X满足二项分布，当n较大而p较小时，X可以近似满足泊松分布。

1.6 超几何概率分布（hypergeometric probability distribution）

超几何概率分布于二项分布联系密切。

这两种概率分布主要有两处不同：在超几何概率分布中，各次试验不是独立的，并且各次试验中成功的概率不等。

超几何概率函数

上述公式说明：

超几何分布中，符号N表示总体容量，r表示总体中具有成功标志的元素的个数，N-r表示总体中具有失败标志的元素的个数。采用不放回抽样方法，从总体中抽取n个元素，超几何概率函数用来计算在这n个元素中恰有x个元素具有成功标志，n-x个元素具有失败标志的概率。

当这种情况出现的时候，我们是从总体的r中抽取到了x个具有成功标志的元素，从N-r中抽取到了n-x个具有失败标志的元素。

  代表从容量N总体中抽出n个元素有多少种不同的抽取方式；

  代表从带有成功标志的总体r中抽出x个成功标志元素有多少种不同的抽取方式；

  代表从带有失败标志的总体N-r中抽出n-x个成功标志元素有多少种不同的抽取方式。

1.7 几何分布（Geometric distribution）

几何分布包含以下条件：

（1）试验由一系列相同的n个试验组成

（2）每次试验由两种可能的结果，即试验结果由两个值构成，其中每个值与一个随机变量对应。我们把其中一个称为成功，另一个称为失败

（3）每次试验成功的概率都是相同的，用p来表示；失败的概率也是相同，用 1 – p表示

（4）试验是相互独立的

几何分布感兴趣的是，为了取得第一次成功需要进行多少次试验。

几何分布概率计算：

说明：p为成功概率，q=1-p为失败概率。如果试验在第r次取得第一次成功，那么首先要失败（r-1）次。

其他概率计算：

（1）需要试验r次以上，才取得第一次成功： 

（2）试验r次或者不到r次取得第一次成功：

几何分布数学期望和方差：

几何分布的众数

当r=1时，几何分布概率P（X=r）达到最大值，所以，任何几何分布的众数都永远是1，因为1是具有最大概率的数。

什么时候使用几何分布？

进行多次相互独立试验时可使用几何分布，每一次试验都存在成功或失败的可能，而你感兴趣的是为了取得第一次成功需要试验多少次。