统计学知识梳理（四）线性回归、卡方分布与方差分析

一、线性回归中的R方误差

假设：
预测值：$\hat{\mathbf{y}}=\left\{{\hat{y}}_1,{\hat{y}}_2,\dots ,{\hat{y}}_n\right\}$
真实值：$\mathbf{y}=\left\{y_1,y_2,\dots ,y_n\right\}$

SSE(和方差、误差平方和)：The sum of squares due to error
MSE(均方差、方差)：Mean
squared error RMSE(均方根、标准差)：Root mean squared error
R-square(确定系数)：Coefficient of determination

一、MSE
均方误差（Mean Square Error）

该统计参数是预测数据和原始数据对应点误差的平方和的均值，也就是SSE/n，和SSE没有太大的区别，计算公式如下

$$MSE=\frac{1}{n}\sum _{i=1}^n{\left({\hat{y}}_i-y_i\right)}^2$$
范围[0,+∞)，当预测值与真实值完全吻合时等于0，即完美模型；误差越大，该值越大。

二、RMSE
均方根误差（Root Mean Square Error）

其实就是MSE加了个根号，这样数量级上比较直观，比如RMSE=10，可以认为回归效果相比真实值平均相差10。

$$RMSE=\sqrt{MSE}=\sqrt{SSE/n}=\sqrt{\frac{1}{n}\sum _{i=1}^n{\left(y_i-{\hat{y}}_i\right)}^2}$$

范围[0,+∞)，当预测值与真实值完全吻合时等于0，即完美模型；误差越大，该值越大。

三、R-square(确定系数)

在讲确定系数之前，我们需要介绍另外两个参数SSR和SST，因为确定系数就是由它们两个决定的
(1)SSR：Sum of squares of the regression，即预测数据与原始数据均值之差的平方和，公式如下
$$SSR=\sum _{i=1}^n{\left(\widehat{y_i}-\overline{y_i}\right)}^2$$

(2)SST：Total sum of squares，即原始数据和均值之差的平方和，公式如下
$$SST=\sum _{i=1}^n{\left(y_i-{\overline{y}}_i\right)}^2$$

SST=SSE+SSR，而我们的“确定系数”是定义为SSR和SST的比值，故

$$R-\text{square}=\frac{SSR}{SST}=\frac{SST-SSE}{SST}=1-\frac{SSE}{SST}$$

其实“确定系数”是通过数据的变化来表征一个拟合的好坏。由上面的表达式可以知道“确定系数”的正常取值范围为[0 1]，越接近1，表明方程的变量对y的解释能力越强，这个模型对数据拟合的也较好。

Python代码

# coding=utf-8
import numpy as np
from sklearn import metrics

# MAPE和SMAPE需要自己实现
def mape(y_true, y_pred):
    return np.mean(np.abs((y_pred - y_true) / y_true)) * 100

def smape(y_true, y_pred):
    return 2.0 * np.mean(np.abs(y_pred - y_true) / (np.abs(y_pred) + np.abs(y_true))) * 100

y_true = np.array([1.0, 5.0, 4.0, 3.0, 2.0, 5.0, -3.0])
y_pred = np.array([1.0, 4.5, 3.5, 5.0, 8.0, 4.5, 1.0])

# MSE
print(metrics.mean_squared_error(y_true, y_pred)) # 8.107142857142858
# RMSE
print(np.sqrt(metrics.mean_squared_error(y_true, y_pred))) # 2.847304489713536
# MAE
print(metrics.mean_absolute_error(y_true, y_pred)) # 1.9285714285714286
# MAPE
print(mape(y_true, y_pred)) # 76.07142857142858
# SMAPE
print(smape(y_true, y_pred)) # 57.76942355889724

二、协方差（Covariance）

$$S_{XY}=\frac{1}{n-1}\sum _{i=1}^n\left(X_i-\overline{X}\right)\left(Y_i-\overline{Y}\right)$$
方差： Var(X) = E[ (X-E(X)) * (X-E(X)) ]
协方差：Cov(X,Y)= E[ (X-E(X)) * (Y-E(Y)) ]
$$\begin{array}{rl}\mathrm{Cov}(X,Y)& =E[(X-E[X])(Y-E[Y])]\\ & =E[XY]-2E[Y]E[X]+E[X]E[Y]\\ & =E[XY]-E[X]E[Y]\end{array}$$
从直观上来看，协方差表示的是两个变量总体误差的期望。

可以通俗的理解为：两个变量在变化过程中是同方向变化？还是反方向变化？同向或反向程度如何？

你变大，同时我也变大，说明两个变量是同向变化的，这时协方差就是正的。

你变大，同时我变小，说明两个变量是反向变化的，这时协方差就是负的。

从数值来看，协方差的数值越大，两个变量同向程度也就越大。反之亦然。

三、卡方分布（Chi-squared Distribution）

1、卡方分布的基本描述：
具有k个自由度的卡方分布是一个由k个独立标准正态随机变量的和所构成的分布。卡方分布经常用于我们常见的卡方检验中。卡方检验一方面可以用来衡量观测分布和理论分布之间的拟合程度，另一方面也可以测量定性数据两个分类标准间的独立性。事实上，卡方检验还有很多其它的作用。
2、卡方分布的定义：
如果Z1，…，Zk是独立标准正态随机变量，那么这些变量的平方和就呈现出了k个自由度的卡方分布。通常，卡方分布可以表示为以下形式。
$$Q\sim {\chi }_k^2$$平方和式子如下
　　　$$X^2=\sum \frac{(O-E{)}^2}{E}$$
其中O代表观察值，E代表期望值。这个检验统计量提供了一种期望值与观察值之间差异的度量办法。最后反映在${\chi }^2$数值的大小上。

要注意的是，卡方分布只有一个参数k，k是一个正整数，表明了分布中自由度的数目。

3、卡方分布表

图中n代表自由度，纵轴为概率值，横轴为卡方值。自由度越大，卡方分布的外形越接近正态分布。

卡方分布临界值表:

第一列为自由度，第一行为显著水平，据此可以查找到临界值，如果检验统计量\chi^{2}大于临界值，则检验统计量就位于拒绝域以内，说明观察结果与期望结果之间的差异显著。

卡方分布有两个主要用途：

（1）用于检验拟合优度，也就是可以检验一组数据与指定曲线的拟合程度，或检验某组观察值是否符合某种分布。

（2）检验两个变量的独立性，通过这个方法检查两个变量之间是否存在某种关联。

参考链接卡方分布Chi-squared Distribution

三、方差分析（ANOVA）

F分布
设X、Y为两个独立的随机变量，X服从自由度为n的卡方分布，Y服从自由度为m的卡方分布，这两个独立的卡方分布除以各自的自由度以后的比率服从F分布。即：$$\mathrm{F}=\frac{X/\mathrm{n}}{Y/\mathrm{m}}$$

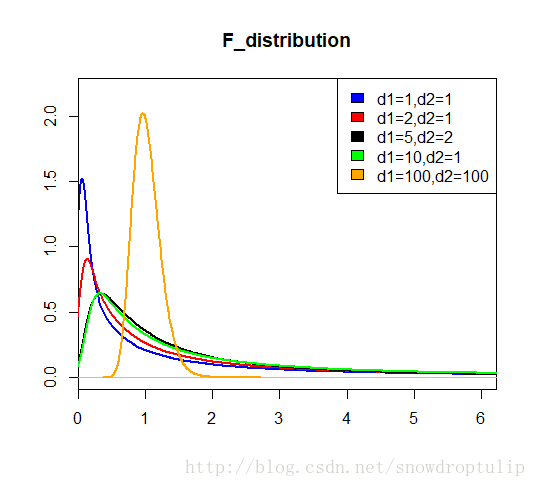
F分布是一种非对称分布；它有两个自由度，即n-1和m-1，相应的分布记为F（ n–1，m-1）， n-1通常称为分子自由度， m-1通常称为分母自由度；F分布是一个以自由度（n-1）和（m-1）为参数的分布族，不同的自由度决定了F 分布的形状。

方差分析
方差分析（ANOVA），又叫F检验

如果计算得到的 F-ratio 或者叫 F-score < critical value（临界值），也即落在绿色区域，则 fail to reject null hypothesis（不能拒绝0假设），反之 F-score > critical value，落在红色区域（rejection region），则 reject null hypothesis（拒绝0假设）。

某已知自由度的 F分布，其 critical value 通过查表得到：

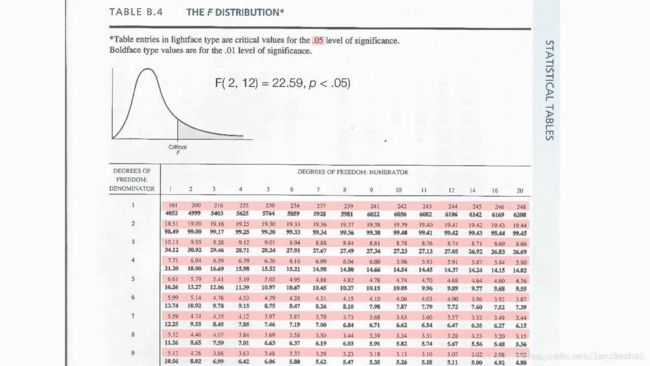
表中红色阴影表示 0.05 的置信水平对应的临界值；
表中黑体数字则在 0.01 的置信水平下对应的临界值；