softmax函数名字的由来(代数&几何原理)——softmax前世今生系列(2)

导读：

softmax的前世今生系列是作者在学习NLP神经网络时，以softmax层为何能对文本进行分类、预测等问题为入手点，顺藤摸瓜进行的一系列研究学习。其中包含：

1.softmax函数的正推原理，softmax的代数和几何意义，softmax为什么能用作分类预测，softmax链式求导的过程。

2.从数学的角度上研究了神经网络为什么能通过反向传播来训练网络的原理。

3.结合信息熵理论，对二元交叉熵为何适合作为损失函数进行了探讨。

通过对本系列的学习，你可以全面的了解softmax的来龙去脉。如果你尚不了解神经网络，通过本系列的学习，你也可以学到神经网络反向传播的基本原理。学完本系列，基本神经网络原理就算式入门了，毕竟神经网络基本的网络类型就那几种，很多变种，有一通百通的特点。

网上对softmax或是神经网络反向传播知识的整理，基本都通过一个长篇大论堆积出来，一套下来面面俱到但又都不精细。本文将每个环节拆开，分别进行详细介绍，即清晰易懂，又减轻了阅读负担，增加可读性。本文也借鉴了其他作者的内容，并列举引用，希望大家在学习过程中能有所收获

本章内容提要：

上一章我们了解了softmax函数的数学推导过程，知道了softmax的表达式为什么长得是这个样子。

本章我们首先从代数表达式的角度上，介绍softmax的演化过程。而后，从几何角度上介绍softmax图形所具有的特点和优点。帮你更好的理解softmax函数的特性。

本章算是softmax的拓展内容，看了之后可以更深刻的理解softmax函数，可以选看。

一、softmax函数回顾

通过对softmax前世今生系(1)的学习，我们知道了softmax的表达式：

                                                                                

而下面我们要介绍的softmax“暂时”长相和它有些不一样：

                                                                                

二者看起来完全不一样，但好像又有点关系的感觉，好像都是e的指数表达式。梅开两朵，各表一枝，他们的相关性我们暂时放下不谈，我们先聊聊g(x, y)这个函数的来源。

二、hardmax的特性

softmax函数其实是从hardmax演变而来的，hardmax函数其实是我们生活中很常见的一种函数，表达式是：

                                                                                 

表达的意思很清楚，从写，y和x中取较大的那个值，为了方便后续比较，我们将hardmax的形式换一下：

                                                                                 

此时，函数本质功能没变，我们只是对定义域做了一个限制，即：

                                                                               

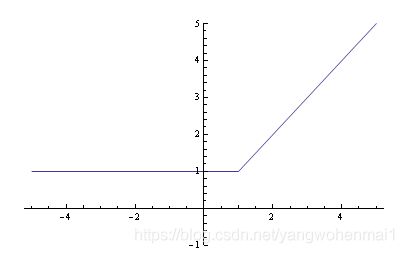
其图形如下：

                                                              

很显然这个函数在 x = 1 处是连续不可导的，可导能帮我们做很多事，那我们有没有办法对他变形，找到一个连续可导的近似函数？

三、softmax和hardmax的相似性

此时就有了softmax函数：

                                                                                 

我们先来看一下这个代数表达式的数学特性。指数函数有一个特点，就是变化率非常快。当x>y时，通过指数的放大作用，会使得二者差距进一步变大，即：

                                                                                         

所以有：

                                                                                        

所以g(x，y)表达式有：

                                                                                 

                                                                                 

因此根据上面的推导过程，g(x，y)约等于x，y中较大的值，即：

                                                                                 

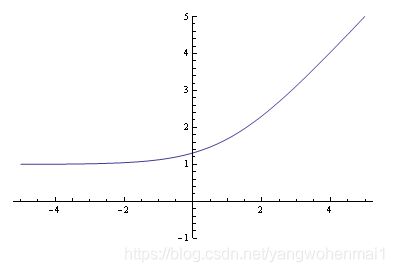
所以我们得出一个结论，g(x，y)是max{x，y}的近似函数，两个函数有相似的数学特性。我们再来看一下softmax函数的图像：

                                                         

很显然这是一个连续且处处可导的函数，这是一个非常重要的特性，g(x，y)即具有与max{x，y}的相似性，又避免了max{x，y}函数不可导的缺点。

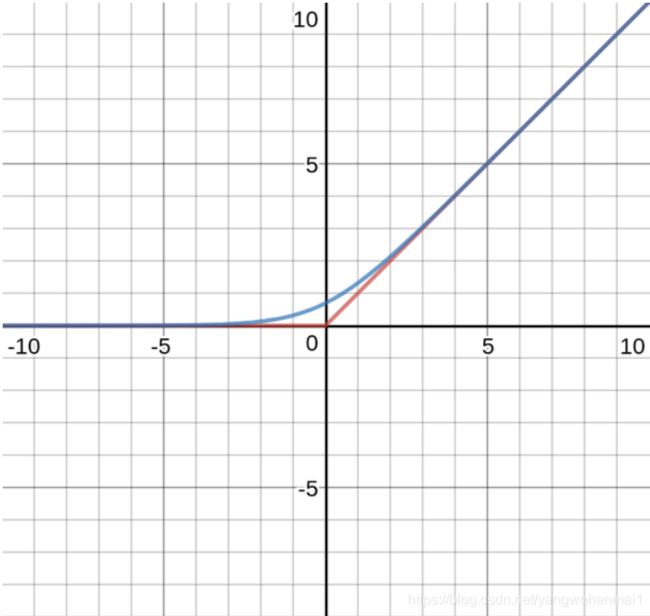
我们把两张图叠加到一起来看看，红色的折线是hardmax函数，他有一个尖尖的棱角，看起来很"hard"。蓝色的弧线看起来就平滑的多，不那么"hard"，这就是softmax函数了。这就时softmax函数名称的由来。

从图上可以看出，当x，y的差别越大时，softmax和hardmax函数吻合度越高。

 

                                                      

 

四、softmax函数概率模型构建

那么回到最初的问题，这个softmax函数和我们神经网络里面做分类层的softmax函数有什么关系呢？

假设我们要从a，b两个未知数字中取一个较大的值，即max{a，b}，那么取到两个数字的概率分别是多少呢？我们可以建立一个概率模型：

1.当a = b的时候，取a，b任意一个数字都可以，所以，取a或者取b的概率各50%。

                                                                              

2.当a = 4，b = 6的时候，b比a更大，因此我们更倾向于取b，那么我们取到b的概率应该会更大一点

                                                                             

                                                                             

3.当a = 8，b = 2的时候，a比b更大，因此我们更倾向于取a，那么我们取到a的概率应该会更大一点

                                                                             

                                                                             

当变量变多时，hardmax就变成了max{s1，s2，s3，s4，...sn}，此时根据我们假设的概率模型，取到每一个样本点的概率就是：

                                                                           

这个的表达式是不是很眼熟？

对于神经网络来说，训练的过程中处理损失调整权重矩阵的时候，需要用到求导。在第二部分我们已经了解到，hardmax函数并不是处处可导的，那么此时就用hardmax的近似函数softmax来代替他，我们已知二者表达式之间的关系：

                                                                       

因此，根据hardmax函数的表达式，得出softmax的概率模型表达式：

                                                                        

以上就是softmax函数的由来，softmax函数是hardmax函数的近似函数，也是对hardmax函数的优化。解决了hardmax函数不可导的问题。因此被广泛的应用在神经网络中。

 

五、总结

文后的笔记中还讨论了softmax在计算中的一些优化方法，后续会单独总结一下。目前重点还是放在对softmax函数特性的分析上。

现在我们已经知道softmax函数的原理和数学上的特性，那么为什么softmax函数可以用在神经网络中，对计算结果进行分类呢？下篇文章我们将介绍softmax函数在神经网络中进行多分类的原理。

传送门：神经网络中的softmax层为何可以解决分类问题——softmax前世今生系列(3)

 

六、附学习笔记如下：

 

参考文献：https://blog.csdn.net/u010127033/article/details/82938888