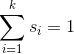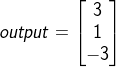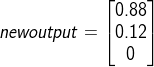神经网络中的softmax层为何可以解决分类问题——softmax前世今生系列(3)
导读:
softmax的前世今生系列是作者在学习NLP神经网络时,以softmax层为何能对文本进行分类、预测等问题为入手点,顺藤摸瓜进行的一系列研究学习。其中包含:
1.softmax函数的正推原理,softmax的代数和几何意义,softmax为什么能用作分类预测,softmax链式求导的过程。
2.从数学的角度上研究了神经网络为什么能通过反向传播来训练网络的原理。
3.结合信息熵理论,对二元交叉熵为何适合作为损失函数进行了探讨。
通过对本系列的学习,你可以全面的了解softmax的来龙去脉。如果你尚不了解神经网络,通过本系列的学习,你也可以学到神经网络反向传播的基本原理。学完本系列,基本神经网络原理就算式入门了,毕竟神经网络基本的网络类型就那几种,很多变种,有一通百通的特点。
网上对softmax或是神经网络反向传播知识的整理,基本都通过一个长篇大论堆积出来,一套下来面面俱到但又都不精细。本文将每个环节拆开,分别进行详细介绍,即清晰易懂,又减轻了阅读负担,增加可读性。本文也借鉴了其他作者的内容,并列举引用,希望大家在学习过程中能有所收获
本章内容提要:
从前两篇文章中,我们了解了softmax函数的基本原理,知道了他为什么叫做softmax,softmax函数有什么特性,以及softmax函数的推导过程。
本文基于前两篇文章的基础上,讲一下为什么我们在做分类预测的时候,经常会选择在神经网络的最后一层的输出结果上,加一个softmax层,来对输出结果进行分类。
一、softmax层和神经网络的关系
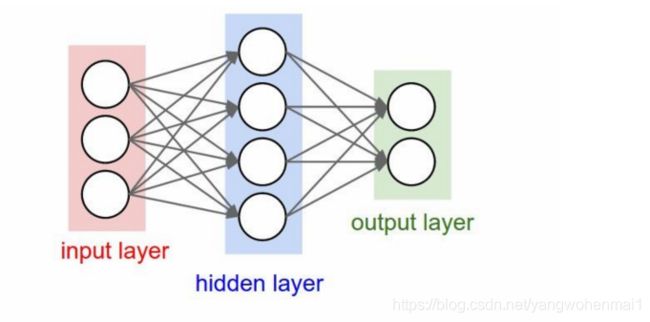
先看一下神经网络的结构:
红色是网络的开端,是输入层。蓝色的部分是网络的隐含层,用于计算。绿色是输出层,输出计算结果 。想了解更多网络内部原理可以参考之前的文章。
那么加上softmax层后的网络形状如下:
在output layer后多出来的一个黑色的layer,就是用于分类的softmax层。最后紫色的new output层就是经过softmax层后,转换成概率的新输出层。
从这个图上可以看出来,softmax层只是对神经网络的输出结果进行了一次换算,将输出结果用概率的形式表现出来。
二、神经网络各层的内部定义
为了方便后续学习,我们对神经网络中每层节点的概念、及节点之间的计算关系介绍一下。因为输入层只做输入数据用,没有计算,图就去掉了。L1层对应隐含层,L2层对应输出层,L2层后链接的就是softmax层,最后输出的S就是经过softmax层转换后的概率输出。
(1)
在隐含层L1中,x是L1上一层的输出结果,也是L1层的输入值,有j个神经元节点,记为:
![]()
(2)
L1层和L2之间的W是权重矩阵,它连接L1层与L2层之间的神经元节点,每两个神经元节点之间由一条权重边链接。其中,L1层的第j个神经元节点x,指向L2层的第i个神经元节点z的权重边w,记为:
![]()
(3)
在输出层L2中,z是L1层的输入值x,与两层之间的权重矩阵W,计算后的结果,记为:
![]()
(4)
z,x,w之间的关系为:
![]()
即如下,(其中b为独立的偏置项,为方便描述,暂不讨论):
![]()
(5)
softmax层对L2层传来的数值进行一个换算,换算公式如下:
![]()
公式的概念及推导过程请看之前的文章:softmax函数的正推原理——softmax前世今生系列(1)。
(6)
s指L2层中,神经元节点z的值,经过softmax层计算后,转换成的概率值,s与z的关系为:
![]()
三、softmax表达式和概率的关系
根据常识我们知道:表述一件事情发生的概率时,一般用百分数来表示。一定发生的事情的概率是100%,不会发生的事情概率是0%.不存在大于100%或者小于0%的概率。一件事情的所有可能性的概率之和等于1.
再来观察一下,输出值经过softmax层计算后的结果表达式:
显然有:
![]()
对所有神经元s求和,可以得到一个结果:
即:
由此可知,输出层的数据,经过softmax函数转换后的结果,即可满足概率表达式的特性。
因此,输出层的数据转化成概率表达式后的输出值,就有了新的意义。对分类问题来说,不同大小的概率值表示,这个结果属于不同类别的可能性大小。
四、示例
引用一张网上的原理图,该图描述了softmax对输出结果的计算过程:
神经网络的输出向量为:
带入softmax计算公式:
通过softmax转换:
通过softmax转换后,结果表达的意思是:这个T向量属于“第一类”的概率是88%,属于“第二类”的概率是12%,属于“第三类”的概率是0%.这就是softmax层在神经网络中,解决分类问题的基本原理。通过softmax函数,将神经网络的输出结果转化成概率表达式。找到最大概率项,为其分类。
五、总结
通过本文学习,我们知道了softmax在神经网络中分类的原理。softmax适用于解决多分类问题,当分类情况只有两种的时候,softmax就转换成了回归问题,也就是二分类问题/逻辑回归/logistic回归。
干脆我们顺手推导一番,当分类结果只有x1和x2两种情况时:
我们来对比一下logistic回归的函数表达式:
咦?突然发现不知不觉中我们竟然把逻辑回归的知识也给学了。不仅如此,其实你马上就要在不知不觉中学会神经网络了。呵呵呵,让我们继续走下去。
通过三篇文章的学习,此时对于softmax函数的概念和基本原理,我们已经基本理清楚了。但实践出真知,softmax函数到底应该怎么用呢?在BP神经网络中,它扮演着什么样的角色?当我们预测的概率结果和正确结果对比有差异时,我们要如何取修正这个神经网络,使得预测的概率更加准确?
当你在思考这些问题时,你已经一只脚踏进了BP神经网络的大门。下一篇文章我们会学习一个叫做交叉熵的东西,我们会明白交叉熵如何帮助我们判断预测结果是否准确,以及如何根据预测结果来修正神经网络参数。
此处是一个小阶段的完结,但也是一个新的开始。有什么问题可以留言问我,如有错误欢迎指正。
相关链接:
softmax函数的正推原理——softmax前世今生系列(1)
softmax函数名字的由来(代数&几何原理)——softmax前世今生系列(2)
六、附学习笔记如下: