最短路径

问题一：只有五行的算法 floyd-warshall

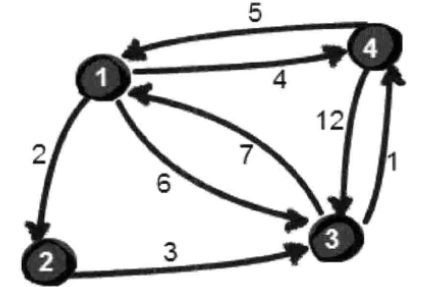
A准备去旅游，有些城市之间有公路，有些则没有，为了节省经费以及计划旅途，A希望知道任意两个城市之间的最短路程

input:

4 8
1 2 2
1 3 6
1 4 4
2 3 3
3 1 7
3 4 1
4 1 5
4 3 12

第一行N M，代表节点数和边数
后面跟着 M 行代表边以及权值

上图中有4个城市8条公路，数字代表公路的长短。
我们需要求任意两个点之间的最短路径，这个问题也叫做“多远最短路径问题”

为了方便理解我们就用邻接矩阵来存储。

---

分析：

如何求任意两个点之间的最短路径呢？
通过之前的学习，我们可以用dfs或者bfs来搜索两个点之间的最短路径
进行 O（n*n）次 bfs 或者 dfs 即可。

有没有其他方法呢？

比如，要让任意两点（a b）之间的路程变短，只能引入第三点（k），通过它进行中转（a k b），才可能缩短ab之间的距离，那么这个 k 是 1~n 之间的哪个点呢？ 甚至有时候不止一个点，而是经过两个或者多个点中转会更短，即 a k1 k2 k3 … b

为了一般化这个问题，当任意两个点之间不允许经过第三个点时，这些城市之间的最短路径就是初始路程

假设目前只允许通过节点 1 ，求任意两个节点之间的最短路径，如何求呢？
只要判断：

e[i][1] + e[1][j] 是否小于 e[i][j] 即可

因此得到：

for (int i = 1; i <= N; i++)
    for (int j = 1; j <= N; j++)
    {q
        if (e[i][j] > e[i][1] + e[1][j])
            e[i][j] = e[i][1] + e[1][j];
    }

这样就更新了通过节点 1 进行中转的情况。然后接着更新 2，3, 4 … n 节点，就能够更新完任意两点之间最终的最短路径。

因此，floyd-warshall 核心代码就五行

for (int k = 1; k <= N; k++)
    for (int i = 1; i <= N; i++)
        for (int j = 1; j <= N; j++)
            if (e[i][j] > e[i][k] + e[k][j])
                e[i][j] = e[i][k] + e[k][j];

时间复杂度：

O( N* N * N)

代码实现：

#include 
#include 


#define MAX 40

#define INF 999999

int graph[MAX + 1][MAX + 1]; 

int N, M;


void floyd_warshall()
{

}


int main()
{
    scanf("%d %d", &N, &M);

    for (int i = 1; i <= N; i++)
        for (int j = 1; j <= N; j++) {
            if (i == j)
                graph[i][j] = 0;
            else
                graph[i][j] = INF;
        }


    for (int k = 1; k <= M; k++) {
        int x, y, weight; 
        scanf("%d %d %d", &x, &y, &weight);

        graph[x][y] = weight;
    }


    //floyd-warshall
    for (int k = 1; k <= N; k++)
        for (int i = 1; i <= N; i++)
            for (int j = 1; j <= N; j++) {

                if (graph[i][k] < INF && graph[k][j] < INF && 
                        graph[i][k] + graph[k][j] < graph[i][j]) 
                    graph[i][j] = graph[i][k] + graph[k][j];
            }


    printf("result is : \n");
    for (int i = 1; i <= N; i++) {
        for (int j = 1; j <= N; j++) {
            if (graph[i][j] == INF) 
                printf("%10d", 0);
            else
                printf("%10d", graph[i][j]);
        }
        printf("\n");
    }

    return 0;
}

问题：

如何表示正无穷？我们这里将 INF 定义为 999999
实际应用中最好评估下最短路径的上限，设置比它稍微大一点即可。
如果你认为正无穷和其他值相加得到一个大于正无穷的数是不被允许的话，在比较的时候添加判断条件就可以了

if (graph[i][k] < INF && graph[k][j] < INF && 
        graph[i][k] + graph[k][j] < graph[i][j]) 
    graph[i][j] = graph[i][k] + graph[k][j];

运行结果：

局限：

floyd-warshall算法不能处理“负权回路”问题。

如果一个图具有“负权回路”，那么这个图没有最短路径。

---

问题二： Dijkstra 算法 - 通过边实现松弛

描述：

如何从指定点（源点）到其余各个定点的最短路径呢？
这个问题也叫做”单源最短路径问题“

比如下图：

求1号点到其余点的最短路径

sample input :

6 9
1 2 1
1 3 12
2 3 9
2 4 3
3 5 5
4 3 4
4 5 13
4 6 15
5 6 4

分析：

”松弛“操作：
对于每个节点 v 来说，我们维持一个属性 v.d ，用来记录从源节点 s 到这个节点 v 的最短路径权重的上界。
我们称 v.d 为 s 到 v 的最短路径估计。

先对于每个节点进行最短路径估计的初始化和前驱节点的初始化： O(V)

INITIALIZE_SINGLE_SOURCE(G, s)
{
    for each vertex v : G.V
        v.d = 无穷大
        v.parent = NIL
    s.d = 0
}

对于每条边 (u, v) 的松弛过程：
首先测试一下是否可以对从 s 到 v 的最短路径进行改善。
测试的方法是：将从 s 到 u 之间的最短距离加上 u 与 v 之间的边权重，并与当前的 s 到 v 的最短路径估计进行比较，如果前者更小，则对 v.d 和 v.parent 进行更新。（简单理解，相当于当前从 s -> u -> v 比 s -> v 更小） 这就是不断对边进行松弛从而达到最短路径的目的，因为最短路径的最优子结构保证了其子距离上也是最短距离。

O( 1 ) 时间的松弛操作：

//松弛操作，尝试通过u来松弛v节点的最短路径
RELAX(u, v, w)
{
    if (v.d > u.d + w(u, v))
        v.d = u.d + w(u, v)
        v.parent = u
}

这里为了简单，我们用一个一维数组 dis 来保存 1 号顶点到其余各个顶点的初试路程：

dis [MAX + 1] = {0}

然后根据边的存储，对dis进行初始化

Dijkstra 基本思想：

每次找到离源点最近的一个顶点，然后以该顶点为中心进行扩展，最终得到源点到其余所有点的最短距离，基本步骤如下：
1. 将所有顶点划分为两个部分： 已知最短路程的点的集合 P 和未知最短路径的顶点集合 Q。 最开始，已知最短路径的顶点集合 P 只有源点一个顶点。 这里用一个数组 book[ MAX + 1]来标识顶点是否被选择即可（也可以用堆、优先队列来优化，这样查找下一个最小点的时候更快）， book[i] = 1 表示已经选择。
2. 设置源点 s 到自己的最短路径为 0 ，即 dis[ start ] = 0，然后根据图的信息对 dis 进行初始化更新。
3. 在集合 Q 中的所有顶点中选择一个离源点 s 最近的点 u （即 dis[ u ] 最小）加入到集合 P，并考察所有以顶点 u 为起点的边， 对每条边进行松弛操作。
4. 重复第三步的过程，直到 Q 集合为空为止。最终 dis 数组中的值就是源点到其余顶点的最短路径。

时间复杂度：

取决于保存集合 Q P 用什么。
这里可以用”优先队列“来存储，每次 insert 和decrease 操作时间为 O（1），每次 extract-min操作时间为 O（V），算法总运行时间是 O（V*V + E）= O （V * V）

如果是系稀疏图，特别， E = o （V*V / lg V），可以使用”二叉堆“来实现最小优先队列，这样每次 extract-min 操作时间为 O（lg V），一共有 | V | 次这样的操作。构建最小二叉堆的成本是 O（V），每次 decrease 的操作为 O（lg V），最多有 | E | 次这样的操作。算法总运行时间是 O （（V+E） * lg V）。若所有节点都可以从源节点到达，则该时间为 O（E * lg V）

也可以用 ”斐波拉契堆“来实现最小优先队列，这样 extract-min 时间为 O（lg V），每次 decrease 操作代价为 O（1）

伪代码：

DIJKSTRA(G, w, s)
{
    INITIALIZE_SINGLE_SOURCE(G, s)

    S = empty  //集合S，保存已经找到最短路径的节点
    Q = G.V  //Q保存的是G的所有节点

    while Q != empty {
        u = EXTRACT_MIN(Q)  //从Q集合中选择出当前最小距离的一个节点u

        S = S + { u }  //将 u 添加到集合S中

        for each vertex v : G.Adj[ u ]  // 对于u的每个邻居节点进行松弛
            RELAX(u, v, w)
    }

}

代码实现：

#include 
#include 

#define MAX 50
#define FAR 9999

void DIJKSTRA(int start);


int A[MAX + 1][MAX + 1];

int book[MAX + 1];

int dist[MAX + 1];

int N;

int start_node;


void DIJKSTRA(int start)
{
    book[start] = 1;

    for (int count = 1; count <= N-1; count++) {
        int u; 
        int min = 999;

        for (int i = 1; i <= N; i++) {
            if (dist[i] == FAR) 
                continue;
            if (dist[i] < min && book[i] == 0) {
                min = dist[i];
                u = i;
            }
        }

        book[u] = 1;

        for (int k = 1; k <= N; k++) {
            if (k == u) 
                continue;
            if (book[k] == 1)
                continue;
            if (A[u][k] == FAR)
                continue;

            if (dist[k] > dist[u] + A[u][k])
                dist[k] = dist[u] + A[u][k];
        }

    }
}



int main()
{
    //read data
    int M;
    scanf("%d %d", &N, &M);

    for (int i = 1; i <= N; i++)
        for (int j = 1; j <= N; j++) {
            if (i == j)
                A[i][j] = 0;
            else
                A[i][j] = FAR;
        }

    for (int i = 1; i <= N; i++)
        book[i] = 0;


    for (int i = 1; i <= M ;i++) {
        int x, y, weight; 
        scanf("%d %d %d", &x, &y, &weight);

        A[x][y] = weight;
    }

    start_node = 1;

    for (int i = 1; i <= N; i++) {
        if (A[start_node][i] == FAR) 
            dist[i] = FAR;
        else
            dist[i] = A[start_node][i];
    }
    //read data end

    DIJKSTRA(start_node);


    for (int i = 1; i <= N; i++) {
        if (dist[i] == FAR) 
            printf("unreachable ");
        else
            printf("%d ", dist[i]);
    }
    printf("\n\n");


    return 0;
}

---

问题三：Bellman-Ford 完美解决负边权

描述：

Dijkstra算法虽然很好，但是基于贪心局部查找，无法解决负边权 边的图，本节我们来学习一个思想和代码上都堪称完美的算法： Bellman-Ford

给定带权重的有向图G，bellman-ford算法返回一个bool值，判断是否存在一个从源点可以到达得权重为负值的环路。
如果存在，算法将告诉我们不存在这样的方案。
如果没有这种环路存在，算法将给出最短路径和它们的权重。

bellman算法通过对边进行“松弛”操作来渐进降低降低从源点s到每个节点v的最短路径的估计值 v.d

样例输入一：（存在）

5 10
1 2 6
1 4 7
2 4 8
2 3 5
3 2 -2
5 3 7
2 5 -4
4 3 -3
4 5 9
5 1 2

样例输入二：（不存在）

8 11
1 2 3
1 3 5
1 4 2
2 5 -4
3 6 6
6 3 -3
4 7 3
7 4 -6
5 8 4
6 8 8
7 8 7

分析：

dijkstra和bellman-ford 都会对边进行松弛操作，“松弛“也是唯一导致最短路径估计和前驱节点发生变化的操作。
不同之处在于，对每条边进行松弛的次数和松弛边的次序有所不同。

Dijkstra 算法和用于有向无环图的最短路径算法，对于每条边仅仅松弛一次。

Bellman-Ford 算法则对于每条边松弛 |V| - 1 次。 （因为任意无环路径中最多包含 |V| 个节点，也就是最多包含 |V| - 1 条边）

时间复杂度：

O(V * E)

代码实现：

伪代码如下：

INITIALIZE_SINGLE_SOURCE(G, s)
{
    for each vertex v : G.V
        v.d = 无穷大
        v.parent = NIL
    s.d = 0
}

//松弛操作，尝试通过u来松弛v节点的最短路径
RELAX(u, v, w)
{
    if (v.d > u.d + w(u, v))
        v.d = u.d + w(u, v)
        v.parent = u
}

BELLMAN_FORD(G, w, s)
{
    INITIALIZE_SINGLE_SOURCE(G, s)

    for i = 1 to |G.V| - 1
        for each edge (u, v) : G.E
            RELAX(u, v , w)

    for each edge (u, v) : G.E //通过u对v进行松弛
        if v.d >  u.d + w(u, v)
            return FALSE
    return TRUE
}

实现：

#include 
#include 

#define MAX 50

#define FAR 99999
#define NIL 0

void INITIALIZE_SINGLE_SOURCE(int start);
void RELAX(int u, int v);
void BELLMAN_FORD(int start);


struct Node {
    int parent;
    int d; 
};


struct Node nodes[MAX + 1];

int A[MAX + 1][MAX + 1];

int N;

int start_node;


void INITIALIZE_SINGLE_SOURCE(int start)
{
    for (int i = 1; i <= N; i++) {
        if (i == start) {
            nodes[i].d = 0;
            nodes[i].parent = NIL;
        } else {
            nodes[i].d = FAR;
            nodes[i].parent = NIL;
        }
    }
}

void RELAX(int u, int v)
{
    if (nodes[u].d == FAR || A[u][v] == FAR)
        return ;

    if (nodes[v].d == FAR || nodes[v].d > nodes[u].d + A[u][v]) {
        nodes[v].d = nodes[u].d + A[u][v];
        nodes[v].parent = u;
        return ;
    }
}

void BELLMAN_FORD(int start) 
{
    INITIALIZE_SINGLE_SOURCE(start);

    for (int count = 1; count <= N - 1; count++) {      //N-1 times
        // relax each edge
        for (int i = 1; i <= N; i++) 
            for (int j = 1; j <= N; j++) {
                if (i == j)
                    continue;
                else
                    RELAX(i, j);
            }
    }

    int flag = 0;
    for (int u = 1; u <= N; u++)
        for (int v = 1; v <= N; v++) {
            if (u == v) 
                continue;

            if (nodes[u].d == FAR || A[u][v] == FAR)
                continue;
            if (nodes[v].d == FAR)
                flag = 1;
            if (nodes[v].d > nodes[u].d + A[u][v])
                flag = 1; 
        }

    if (flag == 1)
        printf("no path..\n");
    else
        printf("path exist..\n");

}


int main()
{
    //input data
    int M;
    scanf("%d %d", &N, &M);

    for (int i = 1; i <= N; i++)
        for (int j = 1; j <= N; j++) {
            if (i == j) 
                A[i][j] = 0;
            else
                A[i][j] = FAR;
        }

    for (int i = 1; i <= M; i++) {
        int x, y, weight; 
        scanf("%d %d %d", &x, &y, &weight);

        A[x][y] = weight;
    }

    start_node = 1;
    //input data


    BELLMAN_FORD(start_node);


    return 0;
}