经典排序算法C++全实现：插入、选择、冒泡、快排、归并、基数，堆排、希尔...

以下代码是个人学习排序算法的一些实践，实现了大部分排序算法的升序版本，并且对每一种算法进行了简要的介绍和复杂度分析。

涉及的算法如下：

1. 插入排序：直接插入排序、折半插入排序、希尔排序
2. 交换排序：冒泡排序、快速排序
3. 选择排序：简单选择排序、堆排序
4. 其他类型：归并排序、基数排序

#include 
#include 
#include 
using namespace std;


// 以下排序均为升序算法
void printArray(vector<int> A){
    for(int i = 0; i < A.size(); i++){
        cout << A[i] << " ";
    }
    cout << endl << endl;
}

/************************************

        插入排序

        1. 直接插入排序
        2. 折半插入排序
        3. 希尔排序（shell）

*************************************/

vector<int> simpleInsertSort(vector<int> A){
    /**
    -- 简单插入排序的思想
    从数组的第二个元素开始，将其选为目标待排序
    认定元素左边的序列为有序，而右边的序列为无序
    将目标元素和左边序列从后向前进行比较，找到插入有序的位置t之后，
    先将该位置之后的元素往后移动1位，然后将目标元素插入到位置t

    空间效率：O（1）
    时间效率：O（n^2)
    最好情况 顺序，O（n）
    最坏情况：逆序，比较次数达到最大，移动次数达到最大
    稳定的排序算法：不会改变相同关键字元素的相对位置。

    适用于顺序存储和链式存储的线性表，适合基本有序和数据量不大的情况
    **/
    if(A.size() <= 1) return A;
    for(int i = 1; i < A.size(); i++){
        if(A[i] < A[i - 1]){
            int tmp = A[i];
            int j = 0;
            for(j = i - 1; j >= 0 && tmp < A[j]; j--)
                A[j + 1] = A[j];
            A[j + 1] = tmp;
        }
    }
    return A;
}

vector<int> binaryInsertSort(vector<int> A){
    /**
    折半插入在简单插入排序的基础上进行了改进
    在向前查找插入位置时使用了二分查找的方法，减少了比较的次数
    折半插入减少了比较的次数，约为 O(nlog2), 元素移动次数没有发生改变O(n^2)
    **/
    int i, j, low, high, mid;
    for(i = 1; i < A.size(); i++){
        int tmp = A[i];
        low = 0;
        high = i - 1;
        while(low <= high){
            mid = (low + high) / 2;
            if(A[mid] > tmp) high = mid-1;
            else low = mid + 1;
        }
        for(j = i - 1; j >= high + 1; j--)
            A[j + 1] = A[j];
        A[high + 1] = tmp;
    }
    return A;
}

vector<int> shellSort(vector<int> A){
    /****
    希尔排序，又称缩小增量排序，由于简单插入排序很适合基本有序的序列，
    那么可以对一些较乱的序列进行处理，使之变为基本有序的序列，
    然后在进行一次直接插入排序。
    思想如下：
    先将数组分割成若干子数组，如[i, i+d, i+2d, i+kd]。
    d为步长，小于，数组长度。这样整个数组就可以分成d个子数组。
    分别对这d个子数组进行直接插入排序。
    进行下一轮，取更小的步长e，重复上述动作，知道步长等于1，在进行一次直接插入排序完成。

    希尔排序是不稳定的，仅适用于顺序存储的线性表
    时间复杂度为O(n^2),空间复杂度为O(1)
    *****/
    for(int d = A.size() / 2; d > 0; d /= 2){
        for(int i = d; i < A.size(); i++){
            int tmp = A[i];
            int j = 0;
            for(j = i; j >= d && A[j - d] > tmp; j -= d)
                A[j] = A[j-d];
            A[j] = tmp;
        }
    }
    return A;
}


/*****************************

        交换排序

        1. 冒泡排序
        2. 快速排序

*****************************/

vector<int> bubbleSort(vector<int> A){
    /***
    冒泡排序是一种简单的通过比较关键字来交换元素的排序方法
    助记码：
     i∈[0,N-1)               //循环N-1遍
        j∈[0,N-1-i)           //每遍循环要处理的无序部分
            swap(j,j+1)          //两两排序（升序/降序）

    空间复杂度分析 常数个辅助单元 O（1）
    最优时间复杂度 O（n）
    最坏时间复杂度 O（n^2）
    平均时间复杂度 O（n^2）

    最坏情况下
    比较次数为： n（n-1）/ 2
    移动次数为：3n（n-1）/2

    属于稳定排序
    ***/
    int i, j;
    for(i = 0; i < A.size() - 1; i++){ // 进行N-1趟比较
        bool flag = false;
        for(j = 0; j < A.size() - 1 - i; j++){
        // 在该趟比较中，0~N-1-i的序列中最大的元素移动到N-2-i的位置
        // 所以下一趟待冒泡的序列不需要考虑已经确定好位置的元素了
        // 冒泡序列需要减1.
            if(A[j] > A[j + 1]){
                int tmp = A[j];
                A[j] = A[j+1];
                A[j+1] = tmp;
                flag = true;
            }
        }
        if(!flag) return A;  // 若未发生交换，则说明排序已经完成
    }

    /* 上面的版本是从前向后比较的版本，这里写一下从后向前比较的版本，依旧是升序
    但不同的是，每趟冒泡总是将冒泡序列最小的元素移动到最前
    for(int i = 0; i < A.size() - 1; i++){
        for(int j = A.size() - 1; j > i; j--){
            if(A[j - 1] > A[j]){
                int tmp = A[j - 1];
                A[j-1] = A[j];
                A[j] = tmp;
            }
        }
    }
    */

    return A;
}


/**********************************************************************
                  快速排序   from wiki:

快速排序使用分治法（Divide and conquer）策略来把一个序列（list）
分为较小和较大的2个子序列，然后递归地排序两个子序列。

步骤为：

1. 挑选基准值：从数列中挑出一个元素，称为“基准”（pivot），
2. 分割：重新排序数列，所有比基准值小的元素摆放在基准前面，
   所有比基准值大的元素摆在基准后面（与基准值相等的数可以到任何一边）。
   在这个分割结束之后，对基准值的排序就已经完成，
3. 递归排序子序列：递归地将小于基准值元素的子序列和
   大于基准值元素的子序列排序。

递归到最底部的判断条件是数列的大小是零或一，此时该数列显然已经有序。


时间复杂度分析！！！

最坏的情况就是每次递归划分时，pivot选取的位置位于子序列的第一个或者最后一个。
T (n) = O(n) + T（1） + T(n-1)
最坏时间复杂度为 O（n^2)  选取的pivot后划分的两个区域大小为n-1,0此时会发生较多的交换操作

平均时间复杂度为 O（nlogn）

最好的情况就是每次划分pivot，恰好位于序列的中间
T(n) = O(n) + 2 T(n/2)
最好时间复杂度为 O（nlogn）选取的pivot恰好满足左边区域小于，右边区域恰好大于。

空间效率分析！！！
由于快排是递归进行的，需要一个递归工作栈来保存每层递归调用的必要信息
其容量应该与递归调用的最大深度一直。
最好情况下栈深度为 log2(n+1)向上取整
最坏情况下栈深度为 n - 1
故最好空间复杂度为 O(logn)
最坏情况下,空间复杂度为O(n)


快排的问题是：
使用递归，空间代价较高
对于小规模数据，还不如插入排序

解决方案：
当递归数据规模充分小，则停止递归，调用一些简单排序如插入排序

这里实现的版本是以每个子表的第一个元素作为pivot。
每趟快速排序，都会将pivot放置在最终合适的位置上

快排是一种不稳定的排序方法，例如，在pivot左边有两个关键字大于pivot且二者相等，
当其进行交换之后，相对位置发生了改变

***************************************************************************/

int partition(vector<int> &A, int low, int high){
    // 划分操作，选定low位置的元素作为pivot，对low~high中的元素进行处理
    // 使得pivot左边元素小于pivot，右边元素小于pivot
    int pivot = A[low];
    while(low < high){
        while(low < high && A[high] >= pivot) high--;  //从后往前数，找到第一个小于pivot的数
        A[low] = A[high];  // 将该数移动到pivot的左边
        while(low < high && A[low] <= pivot) low ++;  //从前往后数，找到第一个大于pivot的数
        A[high] = A[low]; // 将该数移动到pivot的右边
    }
    A[low] = pivot;
    return low;
}

void recursiveQuickSort(vector<int> &A, int low, int high){
    if(low < high){
        int pivotPos = partition(A, low, high);
        recursiveQuickSort(A, low, pivotPos - 1);
        recursiveQuickSort(A, pivotPos + 1, high);
    }
}

vector<int> quickSort(vector<int> A){
    recursiveQuickSort(A, 0, A.size() -1);
    return A;
}


/**** 快排的一个改进 (伪代码)

void QuickSort(vector A, int left, int right){
    cutoff = 50;  // 阈值，当进行快排的区间大于该值时，进行快排
    if(cutoff <= right - left){
        pivot = partition(A, left, right);
        quickSort(A, left, pivot-1);
        quickSort(A, pivot, right);
    }
    else{
        insertSort(A, left, right);  // 区间较小使用简单排序
    }
}

*******/


/**************************

        选择排序

        1. 简单选择排序
        2. 堆排序

***************************/



vector<int> simpleSelectionSort(vector<int> A){
    /**
    简单选择排序

    简单选择算法思想如下：
    假设数组大小为n
    第一趟，选择一个最小的数，选择交换将其放置到位置0，
    第二趟，从位置1开始考虑，从剩下的位置中继续找一个最小的元素，放置到位置1
    如此反复，直到第n-1趟结束。

    时间复杂度为 O(n^2)
    比较次数和序列的初始状态无关，次数为 n（n-1）/2
    不稳定排序
    **/
    int min = 0;
    for(int i = 0; i < A.size() - 1; i++){
        min = i;
        for(int j = i; j < A.size(); j++){
            if(A[j] < A[min]) min = j;
        }
        if(min !=i){
            int tmp = A[i];
            A[i] = A[min];
            A[min] = tmp;
        }
    }
    return A;
}

/***

    堆排序

    在简单选择算法的基础上进行改进，我们可以考虑使用堆来快速查找最小元素

    在排序过程中，我们将数组视为一个完全二叉树顺序存储结构
    利用双亲和孩子结点的关系，快速查找最小或最大元素

    堆的定义如下：
    n个关键字L[1...n]序列称为堆，当且仅当序列满足
    L(i) <= L(2i) && L(i) <= L(2i+1) (小根堆）
    or L(i) >= L(2i) && L(i) >= L(2i+1)  （大根堆）

    算法的过程就是：
    - 将数组建成大根堆
    - 将根头结点和堆底结点交换（将最大值放置到当前数组的末尾）
    - 重新调整剩下的结点，变成大根堆。

    时间复杂度分析
    建立堆时间复杂度为 O（n），之后有n-1次的向下调整的操作
    平均，最好，最坏的时间复杂度都为O(nlogn)

    这里需要了解一下堆的插入和删除操作。

    堆的插入，我们先将元素放置在数组的末尾，对该结点执行向上调整操作
    向上调整的操作就是和父结点比较，如果大于父结点，那么就和父结点对调，继续和新的父结点比较

    删除堆顶元素，那么就让最后一个元素和堆顶交换，删除最后一个结点，然后重新从堆顶向下调整

**/


/***自底向上调整为根大堆***/
vector<int> AdjustDown(vector<int> A, int start, int end){
    int dad = start;
    int son = 2 * dad + 1;
    while(son <= end){
        if(son + 1 <= end && A[son] < A[son+1])
            son++;
        if(A[dad] > A[son]) break;
        else{
            int tmp = A[dad];
            A[dad] = A[son];
            A[son] = tmp;
            dad = son;
            son = 2 * dad + 1;
        }
    }
    return A;
}


/*** 插入堆底元素，需要向上调整 **/
vector<int> AdjustUp(vector<int> A){
    int son = A.size() - 1;
    int dad = son / 2;
    while(son > 0 && A[0] > A[son]){
        if(A[son] > A[dad]){
            int tmp = A[son];
            A[son] = A[dad];
            A[dad] = tmp;
            son = dad;
            dad = son / 2;
        }
    }
    return A;
}


 vector<int> heapSort(vector<int> A){
    // 建立根大堆
    for(int i = A.size() / 2; i >= 0; i--)
        A = AdjustDown(A, i, A.size() - 1);
    // 循环地将根大堆的顶点和堆底进行交换
    for(int i = A.size() - 1; i > 0; i--){
        int tmp = A[0];
        A[0] = A[i];
        A[i] = tmp;
        A = AdjustDown(A, 0, i - 1);
    }
    return A;
 }

/********************************

    归并排序（2路归并排序）

    归并的思想如下：
    一开始把数组看成是n个有序的子表，每个表长度为1
    然后将两个或两个以上的有序表进行组合成一个新的有序表
    得到新的有序表的集合（n/2个），重新两两进行组合排序
    直到最终有序表的个数为1个。

    时间复杂度为 O（nlogn）进行归并需要O（logn）趟，每趟的合并两个有序表的时间复杂度为O(n)

    由于merge操作不会修改两个表中相同关键字的记录次序，所以归并排序是稳定的排序算法

    但是空间复杂度却为O（n）

*********************************/

void Merge(vector<int> &A, vector<int> &B, int low, int mid, int high){
    // 将A中数据全部赋值给B
    for(int k = low; k <= high; k++){
        B[k] = A[k];
    }
    int i = low, j = mid+1, k = i;

    // 合并两个有序表,简单来说就是用两个指针，比较两个指针的大小，将较小的存入A中
    // 然后移动指针
    for(; i <= mid && j <= high; k++){
        if(B[i] < B[j]) A[k] = B[i++];
        else A[k] = B[j++];
    }
    while(i<=mid) A[k++] = B[i++];
    while(j<=high) A[k++] = B[j++];
}

void recursiveMergeSort(vector<int> & A, vector<int> & B,int low, int high){
    if(low < high){
        int mid = (low + high) / 2;
        recursiveMergeSort(A, B, low, mid);
        recursiveMergeSort(A, B, mid + 1, high);
        Merge(A, B, low, mid, high);
    }
}

vector<int> mergeSort(vector<int> A){
    vector<int> B;  // 辅助数组
    for(int i = 0; i < A.size(); i ++){
        B.push_back(0);
    }
    recursiveMergeSort(A, B, 0, A.size() - 1);
    return A;
}

/******************************************************************************

    基数排序

    不是基于比较的排序，而是基于多关键字的排序思想。
    借助分配和收集两种操作对单逻辑关键字完成排序。

    在开始谈基数排序之前，我们得先了解一下桶排序
    假设现在有 N 个整数，其值位于0~100之间，我们要在线性的时间内对其排序
    使用空间换时间的思路，我们可以申请一个长度为M=101的数组A，初始化为0
    读N个整数，记为i，并将其A[i]+= 1.
    然后从头开始遍历数组，读取不为0的A[i]的i，如果A[i]=2就需要读两次，
    这样就完成了线性时间内的排序过程

    但是如果M>>N的话，而且数据不是整数，那么要怎么办呢。

    由此就引申出了基数排序算法。算法分为高位优先MSD和低位优先顺序
    这里只介绍低位优先顺序的实现。

    首先明确基数是什么，此处记为r，简单来说就是要满足进位的数就是基数，如逢十进一，十就是基数

    对于一组数来说，我们可以得到其最大的数所包含的位数K，所有未到达K位的数，我们默认补0
    我们申请 r 个队列来作为桶保存数据（0~r-1），从低位第一位开始考虑，
    分配：如果该位所在的数是 1，那么我们就将其存入队列 1。当所有数都存入队列之后
    收集：将队列中的数从0~1-r中依次首尾连接，构成新的数组，重新上述操作，直到达到最高位，排序完成。


    空间复杂度为 O(r)  r个队列
    时间复杂度O(d(n+r)) 需要d趟收集和分配，一趟分配需要O(n),一趟收集需要O(r)

*******************************************************************************/

int maxBit(vector<int> A){
    // 获取数组中最大数的位数
    if(!A.size()) return 0;
    int maxVal = A[0];
    for(int i = 1; i < A.size(); i++){
        if(A[i] > maxVal){
            maxVal = A[i];
        }
    }
    //  这里假设数都是十位数
    int d = 1;
    int p = 10;
    while(maxVal>=p){
        maxVal /= p;
        ++d;
    }
    return d;
}

vector<int> radixSort(vector<int> A){
    int d = maxBit(A);  //获取最大位数
    int len = A.size();

    int *tmp = new int[len];  // 存取临时数组元素
    int *count = new int[10]; // 计数器
    int radix = 1;
    for(int i = 1; i <= d; i++){
        // 清空计数器
        for(int j = 0; j < len; j++)
            count[j] = 0;

        //按位计入桶
        for(int j = 0; j < len; j++){
            int k = (A[j] / radix) % 10;
            count[k]++;
        }

        // 按位累加计数器，将数转换成排序好数组的位置信息
        for(int j = 1; j < 10; j++)
            count[j] = count[j - 1] + count[j];

        // 按照计数器的位置信息，从后向前将数存入tmp，
        for(int j = len - 1; j >= 0; j--){
            int k = (A[j]  / radix) % 10;
            tmp[count[k] - 1] = A[j];
            count[k]--;
        }

        for(int j = 0; j < len; j++){
            A[j] = tmp[j];
        }
        radix *= 10;
    }
    delete []tmp;
    delete []count;
    return A;
}




int main()
{
    int num = 0;
    vector<int> A;
    int a[10] = {18, 22, 31, 15, 13, 10, 11, 59, 67, 13};
    for(int i = 0; i < 10; i++){
        A.push_back(a[i]);
    }
    cout << "原序列: ";
    printArray(A);

    cout << "简单插入排序: ";
    printArray(simpleInsertSort(A));

    cout << "二分插入排序：";
    printArray(binaryInsertSort(A));

    cout << "希尔排序:";
    printArray(shellSort(A));

    cout << "冒泡排序：";
    printArray(bubbleSort(A));

    cout << "快速排序:";
    printArray(quickSort(A));

    cout << "简单选择排序：";
    printArray(simpleSelectionSort(A));

    cout << "堆排序:";
    printArray(heapSort(A));

    cout << "归并排序:";
    printArray(mergeSort(A));

    cout << "基数排序:";
    printArray(radixSort(A));

    cout <<"原序列:";
    printArray(A);
    return 0;
}

一个简单的测试运行结果：

这里给出一个总结排序算法的速记表，供各位参考。

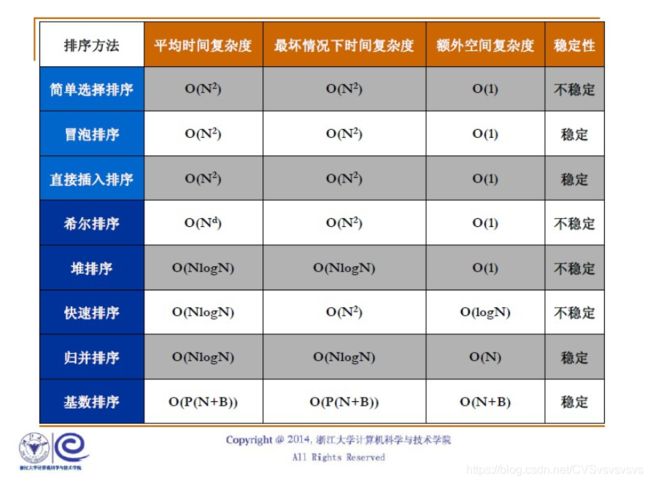
本博客代码来自于个人的一个数据结构与算法的总结项目，汇总了常见的数据结构和算法的实现。
欢迎点此访问！
欢迎大家指正！