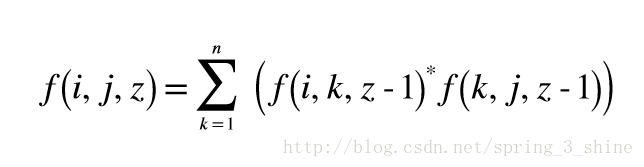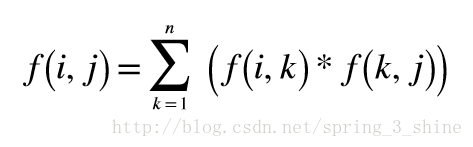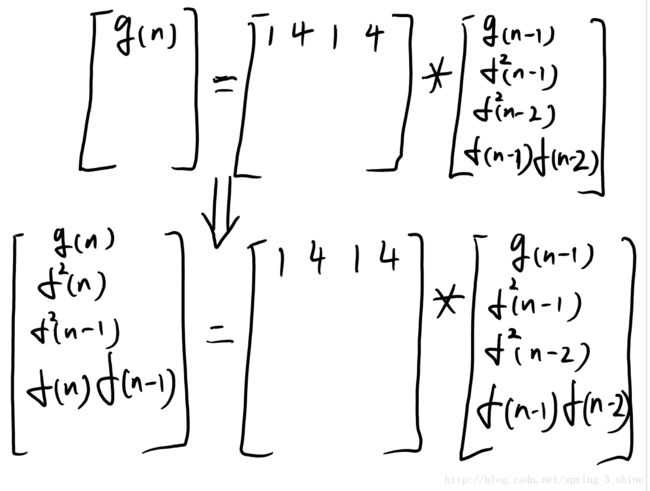矩阵乘法及应用整理

本文参考：
http://www.matrix67.com/blog/archives/276（主要！）
IOI国家集训队2008 俞华程《矩阵乘法在信息学中的应用》（主要！）

因为matrix67大牛的文章出了一些偏差，文章剩余部分在这篇博客里可以找到
https://www.cnblogs.com/frog112111/tag/%E7%9F%A9%E9%98%B5%E7%BB%8F%E5%85%B8%E7%AE%97%E6%B3%95/

https://amoshyc.github.io/ojsolution-build/poj/p3233.html

---

前置技能树

1.两个N阶矩阵相乘：复杂度为N^3，（能优化到更低，但没必要去掌握）
2.快速幂算法：求数a^t，能在 （log t）的复杂度下，得解
3.矩阵快速幂：把矩阵A^k，跟上一个思路一样，不过基础单元a\*a变成了A\*A，复杂度就是矩阵\*快速幂(N^3\* long k)
4.求余运算：（a+b）%c=(a%c+b%c)%c，形状如此。乘法，次方也行

---

类型1：根据矩阵快速幂的定义操作

一： 给定矩阵A，请快速计算出A^n（n个A相乘）的结果，输出的每个数都mod p。

这是裸的矩阵快速幂，点亮前置技能树就能搞。

---

二：給定 NxN 矩陣 A，正整數 K，正整數 M，求 S = A^1 + A^2 + … + A^K。輸出時每個元素要 mod M。

网上有两种思路，
1.采用二分的方式：

首先我们知道，A^i可以二分求出。然后我们需要对整个题目的数据规模k进行二分。比如，当k=6时，有：
A + A^2 + A^3 + A^4 + A^5 + A^6 =(A + A^2 + A^3) + A^3*(A + A^2 + A^3)
应用这个式子后，规模k减小了一半。我们二分求出A^3后再递归地计算A + A^2 + A^3，即可得到原问题的答案。

2.构造矩阵：（容易理解）
https://amoshyc.github.io/ojsolution-build/poj/p3233.html

矩阵构造完成后，从N\*N变为2N\*2N，空间无压力
不想进原文的可以看这张图：

---

类型2：对每个点同时操作，求k次后的个点情况

一：给定n个点，m个操作，构造O(m+n)的算法输出m个操作后各点的位置。操作有平移、缩放、翻转和旋转

这里的操作是对所有点同时进行的。其中翻转是以坐标轴为对称轴进行翻转（两种情况），旋转则以原点为中心。

分析：如果对每个点分别进行模拟，那么m个操作总共耗时O(mn)。
利用矩阵乘法可以在O(m)的时间里把所有操作合并为一个矩阵，然后每个点与该矩阵相乘即可直接得出最终该点的位置，总共耗时O(m+n)。
假设初始时某个点的坐标为x和y，下面5个矩阵可以分别对其进行平移、旋转、翻转和旋转操作。
预先把所有m个操作所对应的矩阵全部乘起来，再乘以(x,y,1)，即可一步得出最终点的位置。

---

二：VOJ1049 题目大意：顺次给出m个置换，反复使用这m个置换对初始序列进行操作，问k次置换后的序列。m<=10, k<2^31。

 因为是顺次置换，可以知道每m次一个循环，将这m个置换“合并”起来（算出这m个置换的乘积），然后接下来我们需要执行这个置换k/m次（取整，若有余数则剩下几步模拟即可）。
 注意任意一个置换都可以表示成矩阵的形式。例如，将1 2 3 4置换为3 1 2 4，相当于下面的矩阵乘法：

---

类型3： 点A到B的方案数

1.给定一个有向图，问从A点恰好走k步（允许重复经过边）到达B点的方案数mod p的值

分析：
如果不能重复经过边，直接暴力搜索就行了，每条边访问一次，复杂度为 O(E)。能重复的话，只能通过k来搜索，这类题k极大，复杂度就很高了。

我们考虑DP,令f(i,j,z)为从i走z步到达j的方案数，那么有

观察形式，发现可以消去z这一维，即：

没错，就是个矩阵乘法，求A^k。

我们得到一个重要结论：无论图怎样变化，求从某一点走到另一个点的确定边数的路径数，只需将每个时刻的图邻接矩阵直接乘起来就得到了答案矩阵。

2.给定一个有向图，问从A点k步内（允许重复经过边）到达B点的方案数mod p的值

这里是k步内，那么就是说求：S = A + A^2 + A^3 + ... + A^k
根据前面的类型一的2，就可以完成了。
注意：
1.到n点后就停止（一般都会这样），将A(n,i~n)置为0。

ps:这里有个神奇的东西，上面那句做完后，将A(n,n)置为1，记为A',最后的矩阵里
（A'^k）[1][n]==S[1][n]
A(n,n)=1可以理解为，到n点就不走了。用矩阵乘法也可以看出来。

---

类型4 构造矩阵求解线性递推关系

构造矩阵呢，所谓规律其实不好用，可以参照“类型1 的二.2”和本类的3，根据逻辑来建立。

1.给定n和p，求第n个Fibonacci数mod p的值，n不超过2^31

根据前面的一些思路，现在我们需要构造一个2 x 2的矩阵，使得它乘以(a,b)得到的结果是(b,a+b)

即是：

2.VOJ 1067 求f(n) = 4f(n-1) – 3f(n-2) + 2f(n-4)

3.HDU 5895 (截取题中的矩阵构造部分)
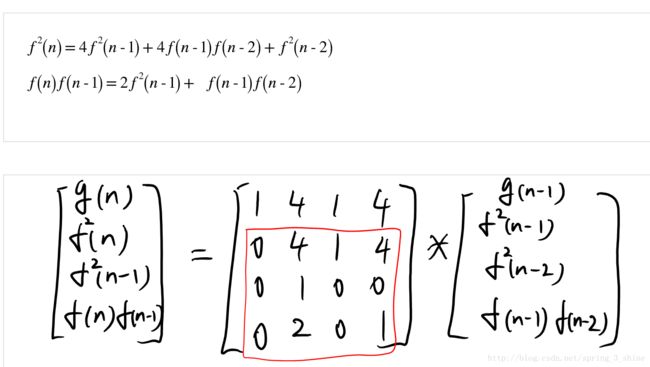
f(n)=2×f(n−1)+f(n−2),f(1)=1,f(0)=0，求：g(n)=f(1)^2+f(2)^2+···+f(n)^2

利用逻辑递推来构造
首先写g(n)的递推公式，利用公式构建下图右边的矩阵等式。

根据矩阵等式右边的模型，补全左边

因为要满足递推的要求，将f(n)^2,f(n)f(n-1)求其递推式，根据递推式补全A矩阵，如下面两图
（ps:这里如果出现新元素，要加到矩阵等式的右边，再重复补全左边，直到不再出现新元素。如果一直循环，那应该是做错了）

类型5 修改矩阵乘法的定义

具体见：IOI国家集训队2008 俞华程《矩阵乘法在信息学中的应用》3.2；3.3；
1.USACO’NOV07
给定一张M条边的无向带权图，求从起点S到终点E恰好经过K条边的最短路径。2 ≤ M ≤ 100, 2 ≤ K ≤ 1000000。保证每个连边的点度至少为2。

这个问题和前面讲的求两点间恰好经过K条边的路径数非常相似。于是，我们也希望能够找到一个类似的矩阵乘法的方法。
这里我们可以修改矩阵的 ‘乘法’函数的定义，
原来是：C[i][j] =  求和：{k:从1到n}  (A[i][k]*B[k,j])
现在是：C[i][j] =  求最小项：{k:从1到n} (A[i][k]+B[k,j])
现在我们就可以用快速幂求解了。
再来看这道题的解法，其实基本模型是floyd算法求最短路。

2.给定一张有向图，求某两点间通过边数恰好为K的路径，使得最大边最小。

这里我们修改‘乘法’定义为：
C[i][j] =  求最小项：{k:从1到n} max(A[i][k],B[k,j])

3. 最小最小边问题：给定一张有向图，求边数恰好为K的路径上最小边最小是多少。

这里我们修改‘乘法’定义为：
C[i][j] =  求最小项：{k:从1到n} min(A[i][k],B[k,j])

4.给定一张有向图，求边数不超过K的路径上最大边最小是多少。

即为，可以在点上停留，修改A[i][i]=-inf，就可以了。

给定一张有向图，求边数在范围K1到K2的路径上最大边最小是多少。(这个纯搬运了)

尽管区间还是可以转化为两个区间的差。但是取最小值操作无法进行做逆运算，换句话说就是知道[0, K2] , [0, K1 − 1]的答案后无法求出[K1, K2]。
我们重新看拓展2，增加一条i到i的权为−∞的边，等价于将图矩阵的主对角线上的值都变成−∞。
从另一个方面来考虑，可以说是把前一个答案保存下来了，因为根据修改过的矩阵乘法的定义：
当k = j时，max {A [i, k] , G [k, j]} = A [i, j]。
即原来的答案，而其他项运算出来的结果就是新的答案。设原矩阵为G0，可以先乘K1个G0，然后再乘K2 − K1个可以保存答案的G，答案也就G0^K1*G^(K2−K1)。
直接使用快速幂，时间复杂度为O(N^3 log K2)。

总结：对DP的优化

其实仔细分析的话，前面几个类型都是DP或者递推，但由于复杂度的问题，采取了矩阵的优化
这类DP本来的复杂度一般是n^2*k，不一定用了矩阵后复杂度会降低，毕竟矩阵的乘法是n^3的操作。
但对于一些题，由于k贼大比如1e8什么的，n较小(N<100)，必须优化。
而矩阵优化过后是n^3*(long k)，就能搞了。

来看俞华程的总结

如果一个动态规划方程能够用矩阵乘法来进行优化，那么必须满足：
1. 状态必须是一维或者两维，如果状态本身有超过两维，可以通过把多维状态压缩到一维的方法降到两维（此时状态数并没有变化）。
2. 每一个状态f [i] [j]必须满足只和f [i − 1] [k]有关，并且只能是线性关系
3. 满足前两条的情况下，可以使用矩阵乘法，但是可能并不能达到优化复杂度的目的。
如果对于不同的i，转移矩阵没有规律，那么是无法使用快速幂来加速矩阵乘法的。通常情况下，都有转移矩阵都相同或者至少是循环出现。

1.经典题目9 用1 x 2的多米诺骨牌填满M x N的矩形有多少种方案，M<=5，N<2^31，输出答案mod p的结果

大牛的图很清晰了，根据上图右边的状态转移式建边，形成的矩阵就是我们所需要的A矩阵。再用快速幂求解。