matlab改进的遗传算法求解路径优化问题
一、引言
遗传算法(GA)是一种全局寻优搜索算法,它首先对问题的可行解进行编码,组成染色体,然后通过模拟自然界的进化过程,对初始种群中的染色体进行选择、交叉和变异,通过一代代进化来找出最优适应值的染色体来解决问题.遗传算法具有很强的全局搜索能力和较强的自适应性,适合解决连续变量函数优化问题和离散变量的优化组合问题。
二、问题描述
旅行商问题(TSP)是一个典型的优化组合问题,它需要求出旅行商从某一城市出发经过所有城市
所给中国30个城市坐标如下:
china=(87 7;91 38;83 46;71 44;64 60;68 58;83 69;87 76;74 78;71 71;58 69;54 62;51 67;37 84;41 94;2 99;7 64;22 60;25 62;18 54;4 50;13 40;18 40;24 42;25 38;41 26;45 21;44 35;58;35;62 32)这里设定交叉概率Pc= 0. 9,变异后概率Pm = 0. 2,初始种群个数s= 250,迭代次数=200,选择个数k(226)=Chrom*GGAP.
所走路程的最短路径,其可能的路径数与城市个数成指数关系增长.目前应用遗传算法解决TSP问题,主要要解决编码问题和算子的设计问题.编码方式约束了运算空间的大小,好的编码方式可以压缩求解空间,提高运算效率.常见的编码方式有二进制编码,实值编码,自然编码等本文主要讨论自然编码方式下算子的改进及其MATLAB的程序实现.针对TSP问题,提出贪婪交叉算子和倒位变异算子来加快算法的收敛速度,同时又不易陷入局部最优,从而较好地解决了群体的多样性和收敛速度的予盾。
三、数学模型
| 符号 | 含义 |
|---|---|
| FitnV | 个体的适应度值 |
| NIND | - |
| NewChrIx | 被选择个体的索引号 |
| Chrom | 种群 |
| GGAP | 代沟 |
| SelCh | 被选择的个体 |
| ObjV | 父代适应度 |
| D | 两两城市之间的距离 |
| MAXGEN | 为停止代数 |
| Rlength | 为路径长度 |
| N | 个体染色体长度 |
| Pm | 变异概率 |
子程序如下
(想要子程序的请关注私聊哦)
- tianma.m
- City Position cross. m
- Distanse.m
- Draw Path. m
- dsxy2fi(坐标)
- Fitness. m
- InitPop. m
- Mutate. m
- OutputPath. m
- PathLength. m
- popmute m
- Recombin. m
- eins. m
- Reverse. m
- Selectm Sus. m
四、主程序
clear
clc
close all
%% 加载数据 %%遗传参数
load CityPosition1;%个城市坐标位置
NIND=250; %种群大小
MAXGEN=200;
Pc=0.9; %交叉概率
Pm=0.2; %变异概率
GGAP=0.9; %代沟(Generation gap)
D=Distanse(X); %生成距离矩阵
N=size(D,1);
%% 初始化种群
Chrom=InitPop(NIND,N);
%% 在二维图上画出所有坐标点
% figure
% plot(X(:,1),X(:,2),'o');
% pause(2)
% %% 画出随机解的路线图
% DrawPath(Chrom(1,:),X)
%
%% 输出随机解的路线和总距离
disp('初始种群中的一个随机值:')
OutputPath(Chrom(1,:));
Rlength=PathLength(D,Chrom(1,:));
disp(['总距离:',num2str(Rlength)]);
disp('~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~')
pause(1)
%% 优化
gen=0;
figure;
hold on;box on
xlim([0,MAXGEN])
title('优化过程')
xlabel('代数')
ylabel('最优值')
ObjV=PathLength(D,Chrom); %计算路线长度
preObjV=min(ObjV);
while gen<MAXGEN
%% 计算适应度
ObjV=PathLength(D,Chrom); %计算路线长度
% fprintf('%d %1.10f\n',gen,min(ObjV))
line([gen-1,gen],[preObjV,min(ObjV)]);pause(0.0001)
preObjV=min(ObjV);
FitnV=Fitness(ObjV);
%% 选择
SelCh=Select(Chrom,FitnV,GGAP);
%% 交叉操作
SelCh=cross(SelCh,FitnV,D);
%% 变异
SelCh=Multate(SelCh,Pm);
%% 重插入子代的新种群
Chrom=Reins(Chrom,SelCh,ObjV);
%% 更新迭代次数
gen=gen+1 ;
end
%% 画出最优解的路线图
ObjV=PathLength(D,Chrom); %计算路线长度
[minObjV,minInd]=min(ObjV);
DrawPath(Chrom(minInd(1),:),X)
%% 输出最优解的路线和总距离
disp('最优解:')
p=OutputPath(Chrom(minInd(1),:));
disp(['总距离:',num2str(ObjV(minInd(1)))]);
disp('-------------------------------------------------------------')
运行结果
得到的结果为:
初始种群中的一个随机值:
14—>15—>2—>8—>27—>30—>9—>13—>26—>16—>18—>11—>29—>5—>20—>21—>25—>23—>22—>1—>3—>7—>12—>17—>19—>6—>4—>24—>28—>10—>14
总距离:1094.9266
最优解:
17—>16—>15—>14—>13—>12—>11—>10—>9—>8—>7—>5—>6—>4—>3—>2—>1—>30—>29—>27—>26—>28—>25—>24—>23—>22—>21—>20—>18—>19—>17
总距离:424.0618
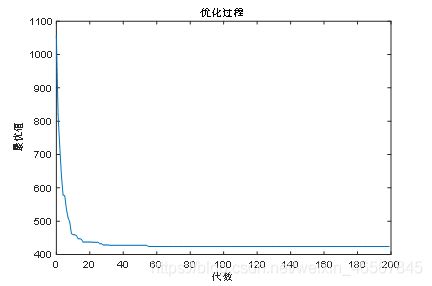
改进后的收敛图
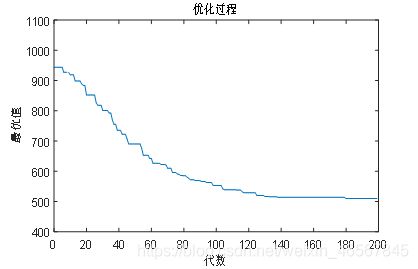
改进前的收敛图
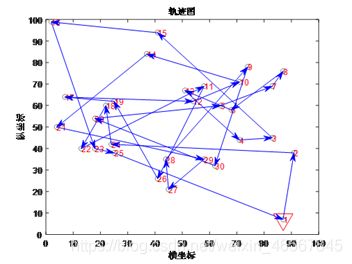
优化后的路径
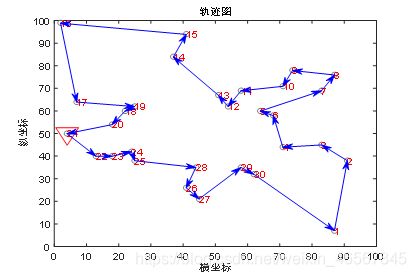
传统的遗传算法在进行140代左右开始趋于平缓,但是最优值较大,进行200次迭代后最优值为510.3231,距离最优解相差甚远,并且图中还有交叉的路线,在图4,5中我们可以看出,改进的遗传算法效率高,收敛速度快,在20到40代之间开始趋于平缓,并且在迭代200次后得到的最优解为424.0618,图中未有交叉路线,说明已经非常接近最好的路线,或者已经达到了最好的路线。