- 数组去重
好奇的猫猫猫
整理自js中基础数据结构数组去重问题思考?如何去除数组中重复的项例如数组:[1,3,4,3,5]我们在做去重的时候,一开始想到的肯定是,逐个比较,外面一层循环,内层后一个与前一个一比较,如果是久不将当前这一项放进新的数组,挨个比较完之后返回一个新的去过重复的数组不好的实践方式上述方法效率极低,代码量还多,思考?有没有更好的方法这时候不禁一想当然有了!!!hashtable啊,通过对象的hash办法
- 回溯算法-重新安排行程
chirou_
算法数据结构图论c++图搜索
leetcode332.重新安排行程这题我还没自己ac过,只能现在凭着刚学完的热乎劲把我对题解的理解记下来。本题我认为对数据结构的考察比较多,用什么数据结构去存数据,去读取数据,都是很重要的。classSolution{private:unordered_map>targets;boolbacktracking(intticketNum,vector&result){//1.确定参数和返回值//2
- Redis系列:Geo 类型赋能亿级地图位置计算
Ly768768
redisbootstrap数据库
1前言我们在篇深刻理解高性能Redis的本质的时候就介绍过Redis的几种基本数据结构,它是基于不同业务场景而设计的:动态字符串(REDIS_STRING):整数(REDIS_ENCODING_INT)、字符串(REDIS_ENCODING_RAW)双端列表(REDIS_ENCODING_LINKEDLIST)压缩列表(REDIS_ENCODING_ZIPLIST)跳跃表(REDIS_ENCODI
- Faiss:高效相似性搜索与聚类的利器
网络·魚
大数据faiss
Faiss是一个针对大规模向量集合的相似性搜索库,由FacebookAIResearch开发。它提供了一系列高效的算法和数据结构,用于加速向量之间的相似性搜索,特别是在大规模数据集上。本文将介绍Faiss的原理、核心功能以及如何在实际项目中使用它。Faiss原理:近似最近邻搜索:Faiss的核心功能之一是近似最近邻搜索,它能够高效地在大规模数据集中找到与给定查询向量最相似的向量。这种搜索是近似的,
- 数据结构之哈希表
X同学的开始
数据结构数据结构散列表
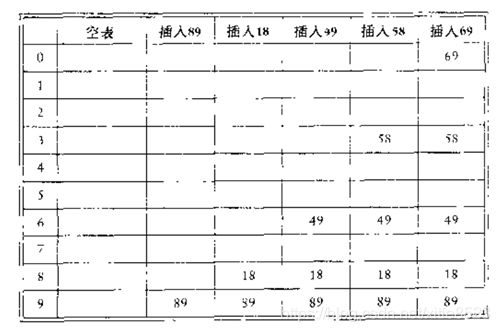
哈希表(散列表)出现的原因在顺序表中查找时,需要从表头开始,依次遍历比较a[i]与key的值是否相等,直到相等才返回索引i;在有序表中查找时,我们经常使用的是二分查找,通过比较key与a[i]的大小来折半查找,直到相等时才返回索引i。最终通过索引找到我们要找的元素。但是,这两种方法的效率都依赖于查找中比较的次数。我们有一种想法,能不能不经过比较,而是直接通过关键字key一次得到所要的结果呢?这时,
- Python开发常用的三方模块如下:
换个网名有点难
python开发语言
Python是一门功能强大的编程语言,拥有丰富的第三方库,这些库为开发者提供了极大的便利。以下是100个常用的Python库,涵盖了多个领域:1、NumPy,用于科学计算的基础库。2、Pandas,提供数据结构和数据分析工具。3、Matplotlib,一个绘图库。4、Scikit-learn,机器学习库。5、SciPy,用于数学、科学和工程的库。6、TensorFlow,由Google开发的开源机
- 数据结构 | 栈和队列
TT-Kun
数据结构与算法数据结构栈队列C语言
文章目录栈和队列1.栈:后进先出(LIFO)的数据结构1.1概念与结构1.2栈的实现2.队列:先进先出(FIFO)的数据结构2.1概念与结构2.2队列的实现3.栈和队列算法题3.1有效的括号3.2用队列实现栈3.3用栈实现队列3.4设计循环队列结论栈和队列在计算机科学中,栈和队列是两种基本且重要的数据结构,它们在处理数据存储和访问顺序方面有着独特的规则和应用。本文将详细介绍栈和队列的概念、结构、实
- [Python] 数据结构 详解及代码
AIAdvocate
算法python数据结构链表
今日内容大纲介绍数据结构介绍列表链表1.数据结构和算法简介程序大白话翻译,程序=数据结构+算法数据结构指的是存储,组织数据的方式.算法指的是为了解决实际业务问题而思考思路和方法,就叫:算法.2.算法的5大特性介绍算法具有独立性算法是解决问题的思路和方式,最重要的是思维,而不是语言,其(算法)可以通过多种语言进行演绎.5大特性有输入,需要传入1或者多个参数有输出,需要返回1个或者多个结果有穷性,执行
- 4.C_数据结构_队列
荣世蓥
数据结构数据结构
概述什么是队列:队列是限定在两端进行插入操作和删除操作的线性表。具有先入先出(FIFO)的特点相关名词:队尾:写入数据的一段队头:读取数据的一段空队:队列中没有数据,队头指针=队尾指针满队:队列中存满了数据,队尾指针+1=队头指针循环队列1、基本内容循环队列是以数组形式构成的队列数据结构。循环队列的结构体如下:typedefintdata_t;//队列数据类型#defineN64//队列容量typ
- C++八股
Petrichorzncu
八股总结c++开发语言
这里写目录标题C++内存管理C++的构造函数,复制构造函数,和析构函数深复制与浅复制:构造函数和析构函数哪个能写成虚函数,为什么?C++数据结构内存排列结构体和类占用的内存:==虚函数和虚表的原理==虚函数虚表(Vtable)虚函数和虚表的实现细节==内存泄漏==指针的工作原理函数的传值和传址new和delete与malloc和freeC++内存区域划分C++11新特性C++常见新特性==智能指针
- 【树一线性代数】005入门
Owlet_woodBird
算法
Index本文稍后补全,推荐阅读:https://blog.csdn.net/weixin_60702024/article/details/141874376分析实现总结本文稍后补全,推荐阅读:https://blog.csdn.net/weixin_60702024/article/details/141874376已知非空二叉树T的结点值均为正整数,采用顺序存储方式保存,数据结构定义如下:t
- python获取子进程返回值_Python对进程Multiprocessing子进程返回值
weixin_39752157
python获取子进程返回值
在实际使用多进程的时候,可能需要获取到子进程运行的返回值。如果只是用来存储,则可以将返回值保存到一个数据结构中;如果需要判断此返回值,从而决定是否继续执行所有子进程,则会相对比较复杂。另外在Multiprocessing中,可以利用Process与Pool创建子进程,这两种用法在获取子进程返回值上的写法上也不相同。这篇中,我们直接上代码,分析多进程中获取子进程返回值的不同用法,以及优缺点。初级用法
- 【数据结构-一维差分】力扣2848. 与车相交的点
hlc@
数据结构数据结构leetcode算法
给你一个下标从0开始的二维整数数组nums表示汽车停放在数轴上的坐标。对于任意下标i,nums[i]=[starti,endi],其中starti是第i辆车的起点,endi是第i辆车的终点。返回数轴上被车任意部分覆盖的整数点的数目。示例1:输入:nums=[[3,6],[1,5],[4,7]]输出:7解释:从1到7的所有点都至少与一辆车相交,因此答案为7。示例2:输入:nums=[[1,3],[5
- JavaScript `Map` 和 `WeakMap`详细解释
跳房子的前端
JavaScript原生方法javascript前端开发语言
在JavaScript中,Map和WeakMap都是用于存储键值对的数据结构,但它们有一些关键的不同之处。MapMap是一种可以存储任意类型的键值对的集合。它保持了键值对的插入顺序,并且可以通过键快速查找对应的值。Map提供了一些非常有用的方法和属性来操作这些数据对:set(key,value):将一个键值对添加到Map中。如果键已经存在,则更新其对应的值。get(key):获取指定键的值。如果键
- 【高阶数据结构】并查集
椿融雪
数据结构与算法数据结构并查集
文章目录一、并查集原理二、并查集实现三、并查集应用一、并查集原理在一些应用问题中,需要将n个不同的元素划分成一些不相交的集合。开始时,每个元素自成一个单元素集合,然后按一定的规律将归于同一组元素的集合合并。在此过程中要反复用到查询某一个元素归属于那个集合的运算。适合于描述这类问题的抽象数据类型称为并查集(union-findset)。比如:某公司今年校招全国总共招生10人,西安招4人,成都招3人,
- python中文版软件下载-Python中文版
编程大乐趣
python中文版是一种面向对象的解释型计算机程序设计语言。python中文版官网面向对象编程,拥有高效的高级数据结构和简单而有效的方法,其优雅的语法、动态类型、以及天然的解释能力,让它成为理想的语言。软件功能强大,简单易学,可以帮助用户快速编写代码,而且代码运行速度非常快,几乎可以支持所有的操作系统,实用性真的超高的。python中文版软件介绍:python中文版的解释器及其扩展标准库的源码和编
- 开发游戏的学习规划
杰克逊的日记
游戏学习
第一阶段:●C#语言快速系统地学习一遍(基础的语法、面向对象、基础的数据结构、基础的设计模式)●Unity的2D和3D部分及UI、动画、物理系统●阶段性测验:需要去用前面所学的这些基础知识来完成一个简单的2d或者3d的案例,将通过一个自制的《Flappybird》游戏案例讲解游戏开发的思想及方法,并将《Flappybird》这个游戏进一步改造成一个横版射击类游戏《Crazybird》以巩固并且升华
- 六、全局锁和表锁:给表加个字段怎么有这么多阻碍
nieniemin
数据库锁设计的初衷是处理并发问题。作为多用户共享的资源,当出现并发访问的时候,数据库需要合理地控制资源的访问规则。而锁就是用来实现这些访问规则的重要数据结构。根据加锁的范围,MySQL里面的锁大致可以分成全局锁、表级锁和行锁三类。6.1全局锁全局锁就是对整个数据库实例加锁。MySQL提供了一个加全局读锁的方法,命令是Flushtableswithreadlock(FTWRL)。当你需要让整个库处于
- Golang Channel
PandaSkr
golang
Channel解析1.Channel源码分析1.1Channel数据结构typehchanstruct{qcountuint//channel的元素数量dataqsizuint//channel循环队列长度bufunsafe.Pointer//指向循环队列的指针elemsizeuint16//元素大小closeduint32//channel是否关闭0-未关闭elemtype*_type//元素类
- ⭐算法入门⭐《归并排序》简单01 —— LeetCode 21. 合并两个有序链表
英雄哪里出来
《LeetCode算法全集》算法数据结构链表c++归并排序
饭不食,水不饮,题必须刷C语言免费动漫教程,和我一起打卡!《光天化日学C语言》LeetCode太难?先看简单题!《C语言入门100例》数据结构难?不存在的!《数据结构入门》LeetCode太简单?算法学起来!《夜深人静写算法》文章目录一、题目1、题目描述2、基础框架3、原题链接二、解题报告1、思路分析2、时间复杂度3、代码详解三、本题小知识一、题目1、题目描述 将两个不降序链表合并为一个新的不降
- 数据结构 1
五花肉村长
数据结构算法开发语言c语言visualstudio
1.什么是数据结构数据结构(DataStructure)是计算机存储和组织数据的方式,是指相互之间存在的一种或多种特定关系的数据元的集合。2.什么是算法算法(Algorithm)就是定义良好的计算过程,他取一个或一组的值为输入,并产生出一个或一组值作为输出。简单来说算法就是一系列的计算步骤,用来将输入数据转化成输出结果。3.数据结构和算法的书籍资料学习完数据结构知识,可以去看《剑指offer》和《
- 【数据结构和算法实践-树-LeetCode113-路径总和Ⅱ】
NeVeRMoRE_2024
数据结构与算法实践数据结构算法leetcodeb树
数据结构和算法实践-树-LeetCode113-路径总和Ⅱ题目MyThought代码示例JAVA-8题目给你二叉树的根节点root和一个整数目标和targetSum,找出所有从根节点到叶子节点路径总和等于给定目标和的路径。叶子节点是指没有子节点的节点输入:root=[5,4,8,11,null,13,4,7,2,null,null,5,1],targetSum=22输出:[[5,4,11,2],[
- 【Python】数据结构,链表,算法详解
AIAdvocate
python数据结构链表排序算法广度优先深度优先
今日内容大纲介绍自定义代码-模拟链表删除节点查找节点算法入门-排序类的冒泡排序选择排序插入排序快速排序算法入门-查找类的二分查找-递归版二分查找-非递归版分线性结构-树介绍基本概述特点和分类自定义代码-模拟二叉树1.自定义代码-模拟链表完整版"""案例:自定义代码,模拟链表.背景: 顺序表在存储数据的时候,需要使用到连续的空间,如果空间不够,就会导致扩容失败,针对于这种情况,我们可以通过链表实现
- AI教你学Python 第4天:函数和模块
凡人的AI工具箱
AI教你学Pythonpython开发语言人工智能AIGC
第四天:数据结构一、什么是数据结构?数据结构是计算机科学中用于组织和存储数据的特定方式。良好的数据结构能够提高数据的访问效率、修改频率和管理能力。Python提供了多种内置数据结构,如列表、元组、字典和集合,便于开发者更有效地处理数据。二、Python中的基本数据结构1.列表(List)定义:列表是一个有序的可变集合,允许重复元素。使用方括号[]表示。#示例:定义一个列表fruits=['appl
- 互联网 Java 工程师面试题(Java 面试题四)
苹果酱0567
面试题汇总与解析java中间件开发语言springboot后端
下面列出这份Java面试问题列表包含的主题多线程,并发及线程基础数据类型转换的基本原则垃圾回收(GC)Java集合框架数组字符串GOF设计模式SOLID抽象类与接口Java基础,如equals和hashcode泛型与枚举JavaIO与NIO常用网络协议Java中的数据结构和算法正则表达式JVM底层Java最佳实JDBCDate,Time与CalendarJava处理XMLJUnit编程现在是时候给
- C# Tuple、ValueTuple
語衣
C#知识补充c#
栏目总目录TupleTuple是C#4.0引入的一个新特性,主要用于存储一个固定数量的元素序列,且这些元素可以具有不同的类型。Tuple是一种轻量级的数据结构,非常适合用于临时存储数据,而无需定义完整的类或结构体。优点简便性:可以快速创建一个包含多个不同类型数据的对象,而无需定义新的类或结构体。灵活性:元素数量和类型在编译时确定,但可以在不同上下文中重复使用不同元素的Tuple。缺点性能:作为引用
- Rust中的所有权和借用规则详解
代码云1
rust开发语言后端
Rust是一种系统编程语言,其设计目标包括内存安全、并发安全以及性能。为了实现这些目标,Rust引入了一系列独特的编程概念,其中最为核心的就是所有权(Ownership)和借用(Borrowing)规则。本文将详细解释Rust中的所有权和借用规则,以及它们如何确保内存安全和并发安全。一、所有权规则在Rust中,每一个值都有一个与之关联的所有者。这个所有者可以是变量、数据结构或者是其他形式的存储。所
- 二叉树--python
电子海鸥
Python数据结构与算法python开发语言数据结构
二叉树一、概述1、介绍是一种非线性数据结构,将数据一分为二,代表根与叶的派生关系,和链表的结构类似,二叉树的基本单元是结点,每个节点包括值和左右子节点引用。每个节点都有两个引用(类似于双向链表),分别指向左子节点和右子节点,该节点被称为这两个子节点的父节点。当给定一个二叉树的结点时,我们将在该节点的左子节点以及其以下结点所形成的树称为左子树,同理,右子节点的部分被称为右子树。在二叉树中,除了叶节点
- 使用WAF防御网络上的隐蔽威胁之反序列化攻击
baiolkdnhjaio
网络安全
什么是反序列化反序列化是将数据结构或对象状态从某种格式转换回对象的过程。这种格式通常是二进制流或者字符串(如JSON、XML),它是对象序列化(即对象转换为可存储或可传输格式)的逆过程。反序列化的安全风险反序列化的安全风险主要来自于处理不受信任的数据源时的不当反序列化。如果应用程序反序列化了恶意构造的数据,攻击者可能能够执行代码、访问敏感数据、进行拒绝服务攻击等。这是因为反序列化过程中可能会自动触
- java 线程池 队列封装_java线程池(线程池组---分离任务队列和线程池)
爱打怪的小魔女
java线程池队列封装
线程池本质上所使用的逻辑模型仍然是我们熟悉的“生产者/消费者”模型。生产消费外部线程(生产者)--->任务消费者和生产者共享一个数据结构(缓存任务)PriorityQueue;生产者将任务添加到队列中,消费者从队列中取出数据;队列和线程池(线程池内部维护一个线程数组),完全耦合在一起,当任务特别多,队列就不断的膨胀,增多,拥堵;就向车子过洞子另外一头走不掉,我靠,长龙(世界最长堵车世界纪录在天朝2
- PHP,安卓,UI,java,linux视频教程合集
cocos2d-x小菜
javaUIPHPandroidlinux
╔-----------------------------------╗┆
- 各表中的列名必须唯一。在表 'dbo.XXX' 中多次指定了列名 'XXX'。
bozch
.net.net mvc
在.net mvc5中,在执行某一操作的时候,出现了如下错误:
各表中的列名必须唯一。在表 'dbo.XXX' 中多次指定了列名 'XXX'。
经查询当前的操作与错误内容无关,经过对错误信息的排查发现,事故出现在数据库迁移上。
回想过去: 在迁移之前已经对数据库进行了添加字段操作,再次进行迁移插入XXX字段的时候,就会提示如上错误。
&
- Java 对象大小的计算
e200702084
java
Java对象的大小
如何计算一个对象的大小呢?
- Mybatis Spring
171815164
mybatis
ApplicationContext ac = new ClassPathXmlApplicationContext("applicationContext.xml");
CustomerService userService = (CustomerService) ac.getBean("customerService");
Customer cust
- JVM 不稳定参数
g21121
jvm
-XX 参数被称为不稳定参数,之所以这么叫是因为此类参数的设置很容易引起JVM 性能上的差异,使JVM 存在极大的不稳定性。当然这是在非合理设置的前提下,如果此类参数设置合理讲大大提高JVM 的性能及稳定性。 可以说“不稳定参数”
- 用户自动登录网站
永夜-极光
用户
1.目标:实现用户登录后,再次登录就自动登录,无需用户名和密码
2.思路:将用户的信息保存为cookie
每次用户访问网站,通过filter拦截所有请求,在filter中读取所有的cookie,如果找到了保存登录信息的cookie,那么在cookie中读取登录信息,然后直接
- centos7 安装后失去win7的引导记录
程序员是怎么炼成的
操作系统
1.使用root身份(必须)打开 /boot/grub2/grub.cfg 2.找到 ### BEGIN /etc/grub.d/30_os-prober ### 在后面添加 menuentry "Windows 7 (loader) (on /dev/sda1)" {
- Oracle 10g 官方中文安装帮助文档以及Oracle官方中文教程文档下载
aijuans
oracle
Oracle 10g 官方中文安装帮助文档下载:http://download.csdn.net/tag/Oracle%E4%B8%AD%E6%96%87API%EF%BC%8COracle%E4%B8%AD%E6%96%87%E6%96%87%E6%A1%A3%EF%BC%8Coracle%E5%AD%A6%E4%B9%A0%E6%96%87%E6%A1%A3 Oracle 10g 官方中文教程
- JavaEE开源快速开发平台G4Studio_V3.2发布了
無為子
AOPoraclemysqljavaeeG4Studio
我非常高兴地宣布,今天我们最新的JavaEE开源快速开发平台G4Studio_V3.2版本已经正式发布。大家可以通过如下地址下载。
访问G4Studio网站
http://www.g4it.org
G4Studio_V3.2版本变更日志
功能新增
(1).新增了系统右下角滑出提示窗口功能。
(2).新增了文件资源的Zip压缩和解压缩
- Oracle常用的单行函数应用技巧总结
百合不是茶
日期函数转换函数(核心)数字函数通用函数(核心)字符函数
单行函数; 字符函数,数字函数,日期函数,转换函数(核心),通用函数(核心)
一:字符函数:
.UPPER(字符串) 将字符串转为大写
.LOWER (字符串) 将字符串转为小写
.INITCAP(字符串) 将首字母大写
.LENGTH (字符串) 字符串的长度
.REPLACE(字符串,'A','_') 将字符串字符A转换成_
- Mockito异常测试实例
bijian1013
java单元测试mockito
Mockito异常测试实例:
package com.bijian.study;
import static org.mockito.Mockito.mock;
import static org.mockito.Mockito.when;
import org.junit.Assert;
import org.junit.Test;
import org.mockito.
- GA与量子恒道统计
Bill_chen
JavaScript浏览器百度Google防火墙
前一阵子,统计**网址时,Google Analytics(GA) 和量子恒道统计(也称量子统计),数据有较大的偏差,仔细找相关资料研究了下,总结如下:
为何GA和量子网站统计(量子统计前身为雅虎统计)结果不同?
首先:没有一种网站统计工具能保证百分之百的准确出现该问题可能有以下几个原因:(1)不同的统计分析系统的算法机制不同;(2)统计代码放置的位置和前后
- 【Linux命令三】Top命令
bit1129
linux命令
Linux的Top命令类似于Windows的任务管理器,可以查看当前系统的运行情况,包括CPU、内存的使用情况等。如下是一个Top命令的执行结果:
top - 21:22:04 up 1 day, 23:49, 1 user, load average: 1.10, 1.66, 1.99
Tasks: 202 total, 4 running, 198 sl
- spring四种依赖注入方式
白糖_
spring
平常的java开发中,程序员在某个类中需要依赖其它类的方法,则通常是new一个依赖类再调用类实例的方法,这种开发存在的问题是new的类实例不好统一管理,spring提出了依赖注入的思想,即依赖类不由程序员实例化,而是通过spring容器帮我们new指定实例并且将实例注入到需要该对象的类中。依赖注入的另一种说法是“控制反转”,通俗的理解是:平常我们new一个实例,这个实例的控制权是我
- angular.injector
boyitech
AngularJSAngularJS API
angular.injector
描述: 创建一个injector对象, 调用injector对象的方法可以获得angular的service, 或者用来做依赖注入. 使用方法: angular.injector(modules, [strictDi]) 参数详解: Param Type Details mod
- java-同步访问一个数组Integer[10],生产者不断地往数组放入整数1000,数组满时等待;消费者不断地将数组里面的数置零,数组空时等待
bylijinnan
Integer
public class PC {
/**
* 题目:生产者-消费者。
* 同步访问一个数组Integer[10],生产者不断地往数组放入整数1000,数组满时等待;消费者不断地将数组里面的数置零,数组空时等待。
*/
private static final Integer[] val=new Integer[10];
private static
- 使用Struts2.2.1配置
Chen.H
apachespringWebxmlstruts
Struts2.2.1 需要如下 jar包: commons-fileupload-1.2.1.jar commons-io-1.3.2.jar commons-logging-1.0.4.jar freemarker-2.3.16.jar javassist-3.7.ga.jar ognl-3.0.jar spring.jar
struts2-core-2.2.1.jar struts2-sp
- [职业与教育]青春之歌
comsci
教育
每个人都有自己的青春之歌............但是我要说的却不是青春...
大家如果在自己的职业生涯没有给自己以后创业留一点点机会,仅仅凭学历和人脉关系,是难以在竞争激烈的市场中生存下去的....
&nbs
- oracle连接(join)中使用using关键字
daizj
JOINoraclesqlusing
在oracle连接(join)中使用using关键字
34. View the Exhibit and examine the structure of the ORDERS and ORDER_ITEMS tables.
Evaluate the following SQL statement:
SELECT oi.order_id, product_id, order_date
FRO
- NIO示例
daysinsun
nio
NIO服务端代码:
public class NIOServer {
private Selector selector;
public void startServer(int port) throws IOException {
ServerSocketChannel serverChannel = ServerSocketChannel.open(
- C语言学习homework1
dcj3sjt126com
chomework
0、 课堂练习做完
1、使用sizeof计算出你所知道的所有的类型占用的空间。
int x;
sizeof(x);
sizeof(int);
# include <stdio.h>
int main(void)
{
int x1;
char x2;
double x3;
float x4;
printf(&quo
- select in order by , mysql排序
dcj3sjt126com
mysql
If i select like this:
SELECT id FROM users WHERE id IN(3,4,8,1);
This by default will select users in this order
1,3,4,8,
I would like to select them in the same order that i put IN() values so:
- 页面校验-新建项目
fanxiaolong
页面校验
$(document).ready(
function() {
var flag = true;
$('#changeform').submit(function() {
var projectScValNull = true;
var s ="";
var parent_id = $("#parent_id").v
- Ehcache(02)——ehcache.xml简介
234390216
ehcacheehcache.xml简介
ehcache.xml简介
ehcache.xml文件是用来定义Ehcache的配置信息的,更准确的来说它是定义CacheManager的配置信息的。根据之前我们在《Ehcache简介》一文中对CacheManager的介绍我们知道一切Ehcache的应用都是从CacheManager开始的。在不指定配置信
- junit 4.11中三个新功能
jackyrong
java
junit 4.11中两个新增的功能,首先是注解中可以参数化,比如
import static org.junit.Assert.assertEquals;
import java.util.Arrays;
import org.junit.Test;
import org.junit.runner.RunWith;
import org.junit.runn
- 国外程序员爱用苹果Mac电脑的10大理由
php教程分享
windowsPHPunixMicrosoftperl
Mac 在国外很受欢迎,尤其是在 设计/web开发/IT 人员圈子里。普通用户喜欢 Mac 可以理解,毕竟 Mac 设计美观,简单好用,没有病毒。那么为什么专业人士也对 Mac 情有独钟呢?从个人使用经验来看我想有下面几个原因:
1、Mac OS X 是基于 Unix 的
这一点太重要了,尤其是对开发人员,至少对于我来说很重要,这意味着Unix 下一堆好用的工具都可以随手捡到。如果你是个 wi
- 位运算、异或的实际应用
wenjinglian
位运算
一. 位操作基础,用一张表描述位操作符的应用规则并详细解释。
二. 常用位操作小技巧,有判断奇偶、交换两数、变换符号、求绝对值。
三. 位操作与空间压缩,针对筛素数进行空间压缩。
&n
- weblogic部署项目出现的一些问题(持续补充中……)
Everyday都不同
weblogic部署失败
好吧,weblogic的问题确实……
问题一:
org.springframework.beans.factory.BeanDefinitionStoreException: Failed to read candidate component class: URL [zip:E:/weblogic/user_projects/domains/base_domain/serve
- tomcat7性能调优(01)
toknowme
tomcat7
Tomcat优化: 1、最大连接数最大线程等设置
<Connector port="8082" protocol="HTTP/1.1"
useBodyEncodingForURI="t
- PO VO DAO DTO BO TO概念与区别
xp9802
javaDAO设计模式bean领域模型
O/R Mapping 是 Object Relational Mapping(对象关系映射)的缩写。通俗点讲,就是将对象与关系数据库绑定,用对象来表示关系数据。在O/R Mapping的世界里,有两个基本的也是重要的东东需要了解,即VO,PO。
它们的关系应该是相互独立的,一个VO可以只是PO的部分,也可以是多个PO构成,同样也可以等同于一个PO(指的是他们的属性)。这样,PO独立出来,数据持
![]() ,这个函数对每个X都会计算出一个值,而不是和二次函数一样探测同样的位置。比较常见的是
,这个函数对每个X都会计算出一个值,而不是和二次函数一样探测同样的位置。比较常见的是![]() 作为冲突函数,即散列函数为
作为冲突函数,即散列函数为![]() 。
。![]() 的选择也十分重要,显然,函数结果一定不能为0.与
的选择也十分重要,显然,函数结果一定不能为0.与![]() 类似,
类似,![]() 也可以是求余的形式,如
也可以是求余的形式,如![]() =R - (X mod R)。如下面的例子
=R - (X mod R)。如下面的例子![]()
![]()
![]()