python3实现归并排序算法图文详解
归并排序做为一种比较经典的排序思路,经常在面试中被提及。即使不直接考察也会换种方式涉及,例如很常见的20G超大文件排序问题。这一节就分解下归并的思路,最后用代码实现一下。下一篇我们进行一下扩展,实现超大文件的排序。
文章目录
-
- 归并排序
- 代码实现
- 时间复杂度
- 稳定性
- 接下来
归并排序
归并排序(Merge Sort)的主要思想就是化整为零,分批治理,再逐层合并结果。和快排有些许类似,同样也是递归的典型使用场景。
例如有下面的list
[38,67,26,11,99,20,45,54]
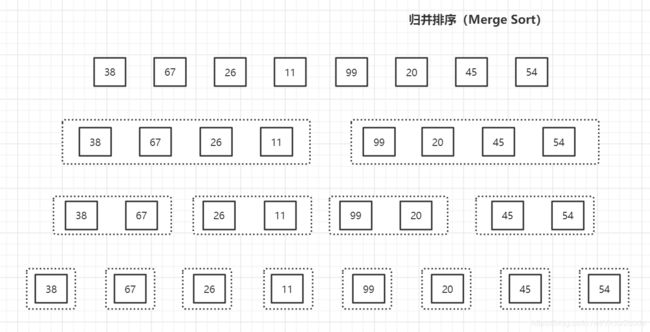
首先是化整为零,分的方法很多,我这里采用对半分
一直分到最后每个list只有单个元素为止,然后按照原先分的list开始从下往上合并。
即使是奇数个元素也是可以对半分的,一直分到最后3个元素分到一边1个一边2个,其中的2个元素再分为两个单元素
每个list分解再合并之后就变成了有序list,拿其中一部分来举例

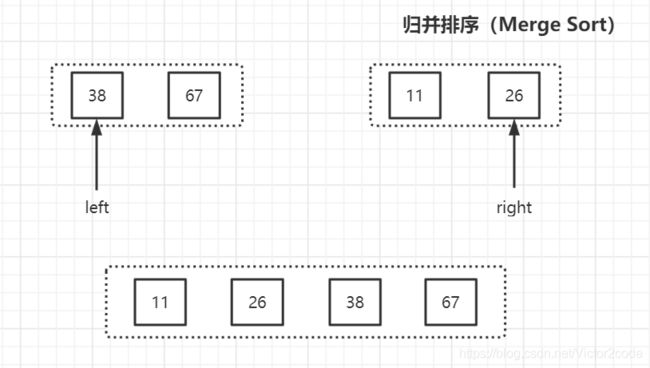
第二行的两个list经过再合并就变成了如下的有序list,因为从第三行合并到第二行和从第二行合并到第一行的算法是一样的,所以我们就以已经排序完成的第二行到第一行为例来说明
对左右两个list的第一个元素分别放置游标,并且比较俩游标元素的大小,较小的放入新list,并且该侧的游标往右移动一位。因为11比38小,所以将11放入新list,并且right游标往右移动到26。
此时26还是比38小,所以还是将26放入新list,往右移动right游标,但是此时已经无法移动。之后将另一个list的元素全部添加到新list的尾部。
这样就将原先的[38,67,26,11]经过先拆分再合并的方式排序成了[11,26,38,67]。之后该新list又和之前拆分的另一个list进行同样的操作往上合并,一直到最后恢复完整list。
代码实现
要实现的功能,就是传递一个list进去,能返回一个有序list。以上面的图片为例,实现从[38,67,26,11]到[11,26,38,67]。
按照递归的思路,我们这里只需要关心从第二层到第一层的拆分再合并的实现,至于再往下直接用递归操作即可。
将原list拆分为2段,每段经过原函数递归返回俩有序list
def mergeSort(list_):
list1 = mergeSort(list_[0:len(list_)//2])
list2 = mergeSort(list_[len(list_)//2:])
这里使用的是python3中的整除语法//,此时的list1和list2就分别是已经排好序的子list。
下面先考虑退出递归的条件,也就是传递进来的list_长度为1的时候,此时直接返回原list即可
def mergeSort(list_):
if len(list_)==1:
return list_
list1 = mergeSort(list_[0:len(list_)//2])
list2 = mergeSort(list_[len(list_)//2:])
然后来实现通用状况,通过创建两个游标来实现一个新list
def mergeSort(list_):
if len(list_)==1:
return list_
list1 = mergeSort(list_[0:len(list_)//2])
list2 = mergeSort(list_[len(list_)//2:])
left = 0
right = 0
new_list = []
while True:
if list1[left] <= list2[right]:
new_list.append(list1[left])
left += 1
if left == len(list1):
new_list+=list2[right:]
break
else:
new_list.append(list2[right])
right += 1
if right == len(list2):
new_list+=list1[left:]
break
return new_list
if __name__ == '__main__':
result = mergeSort([38,67,26,11])
print(result) # [11,26,38,67]
成功完成。这里为了保持稳定性,将相等的情况也是取得左边得list中的元素。同时要注意这里和快速排序不同的是,快速排序是直接操作原list,这里是返回新的list。
当然,代码通常需要低耦合,于是可以把其中对俩list进行合并的部分单独拎出来写成函数,结构更清晰
def mergeSort(list_):
if len(list_)==1:
return list_
list1 = mergeSort(list_[0:len(list_)//2])
list2 = mergeSort(list_[len(list_)//2:])
return combine(list1,list2)
def combine(list1,list2):
left = 0
right = 0
new_list = []
while True:
if list1[left] <= list2[right]:
new_list.append(list1[left])
left += 1
if left == len(list1):
new_list += list2[right:]
break
else:
new_list.append(list2[right])
right += 1
if right == len(list2):
new_list += list1[left:]
break
return new_list
if __name__ == '__main__':
result = mergeSort([38,67,26,11,99,20,45,54])
print(result) # [11, 20, 26, 38, 45, 54, 67, 99]
时间复杂度
先来看上面的combine函数,最坏情况相当于list1和list2都遍历到了最后,也就是等于两个list的长度和。所以从下往上进行合并的时候,每一层的最坏时间复杂度都是list的长度n。
只需要再乘以总的拆分次数即可。对半分到最后的总次数是logn,所以总的时间复杂度是O(nlogn)。
归并算法的时间复杂度虽然小,但是因为产生了新的list,所以空间复杂度要差一些。
稳定性
从上面的等于号取左边list可以看出来,原先在左边的值最终还是在左边,算法稳定。
接下来
下一篇博客我们来对归并算法进行扩充,来处理面试中遇到的20G大文件的排序问题。
补充阅读:《python3实现快速排序算法图文详解》
我是T型人小付,一位坚持终身学习的互联网从业者。喜欢我的博客欢迎在csdn上关注我,如果有问题欢迎在底下的评论区交流,谢谢。