须知
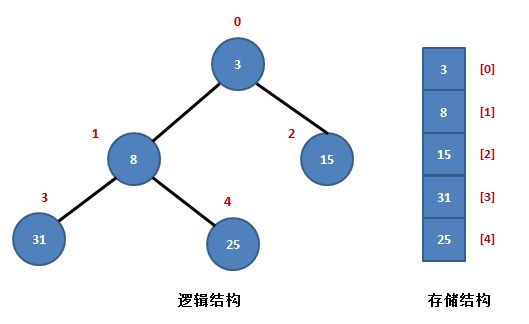
如果想了解堆排序算法,必须知道先了解二叉树和完全二叉树
然后,我们再了解一下,什么是堆?
堆是是顺序存储的完全二叉树。
过程
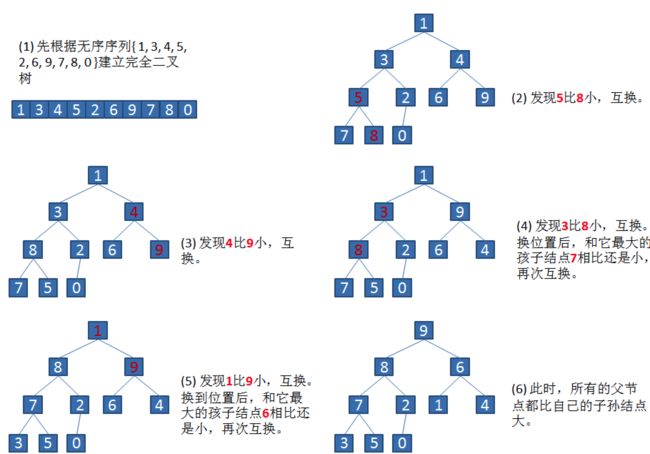
- 把一个无序数列,转化成一个大根堆
- 把最后一个元素和根元素交换,然后取出最后一个元素到一个特定的list中。然后把剩下的数列再次调整为一个大根堆
- 重复1,2步骤,直到list中只有一个元素,直接放到我们之前说到的特定的list中即可。(特定的list就是排序之后的数列了)
无序数列转化成大根堆过程
迭代1.2 过程(包含了取出根的过程)
Code
def adjust_heap(l, parent):
length = len(l)
parent_value = l[parent]
child = parent * 2 + 1
while child < length:
if child + 1 < length and l[child + 1] > l[child]:
child += 1
if l[child] <= parent_value:
break
l[parent] = l[child]
parent = child
child = 2 * parent + 1
l[parent] = parent_value
def heap_sort(l, result=None):
if len(l) == 1:
result.append(l[0])
return l
if result is None:
result = []
parents = [i for i in range(len(l))]
parents.reverse()
for parent in parents:
adjust_heap(l, parent)
tmp = l[0]
l[0] = l[len(l) - 1]
l[len(l) - 1] = tmp
result.append(l.pop())
heap_sort(l, result)
return result
Test
def test():
l = [99,7, 4, 5, 3, 6, 9, 7, 8, 0]
print l
print heap_sort(l)