吴恩达机器学习练习3：Logistic regression(Multi-class Classification)

ex3的第一小节是扩充之前的logistic regression算法，并将其应用到多分类器中。
1、数据集
文件ex3data1.mat中包含了5000个手写数字训练样本，每个数字图像含有2020个灰度像素值，使用浮点数来代替每个位置的灰度级，每个图像存储为400维矢量。文件ex3data1.mat含有矩阵X和矢量y，其中X维度为5000400，y的维度为5000*1，每个训练样本（手写数字图像）均为矩阵X的1行，则矩阵X可以表示为：

矢量y为训练集的标签，其每行的数据代表的是对应X矩阵中对应行的训练样本代表的数值，即0-9。由于在matlab中没有偏移量index0，因此，将标签值’0’修改为’10’，即y中数值实际为1-10，其中10代表0。

load('ex3data1.mat'); % training data stored in arrays X, y

2、原始数据的可视化

clear ; close all; clc

input_layer_size  = 400;  % 20x20 Input Images of Digits，输入点数为400
num_labels = 10;          % 10 labels, from 1 to 10，输出点数为10
                          % (note that we have mapped "0" to label 10)

% Load Training Data
fprintf('Loading and Visualizing Data ...\n')

load('ex3data1.mat'); % training data stored in arrays X, y
m = size(X, 1);%m为X的总行数，即训练样本的个数

% Randomly select 100 data points to display
rand_indices = randperm(m);%随机打乱1-m，得到一个序列
sel = X(rand_indices(1:100), :);

displayData(sel);

fprintf('Program paused. Press enter to continue.\n');
pause;

rand_indices = randperm(m)该语句的意思是随机打乱数据1-m，并得到该序列，其返回值为一个行向量。
rand_indices(1:100)获取随机序列的前100位，其实际就是从1-m中随机抽取100个数据
sel = X(rand_indices(1:100), ?;将随机序列作为索引从矩阵X中抽取对应的行向量，即从训练集中随机抽取100个训练样本。
其中sel为100400的矩阵。

3、矢量化的logistic regression算法
由于要分成10类，正常情况下应该进行10次独立的logistic regression算法，矢量化算法可以减少代码。
（1）矢量化代价函数
在ex2中代价函数为：

其中：


可以重新定义矩阵X和theta以快速计算：


矩阵X为m×n矩阵，m个样本，每个样本有n个特征值。则Xtheta为m×1矩阵。
sigmoid(Xtheta)为m×1矩阵，每行均为每个样本的拟合值。
由于存在求和，而y为列向量，则可以采用转置相乘的方式求和，可以得到代码为：

J = (y'*log(sigmoid(X*theta))+(1-y)'*log(1-sigmoid(X*theta)))/(-m);

执行代码，其结果为：

Testing lrCostFunction() with regularization
Cost: 0.734819
Expected cost: 2.534819

此处还未进行正则化，固与期望的结果不一致。
（2）矢量化梯度函数
在ex2中，其梯度计算函数为：

对其进行矢量化有：

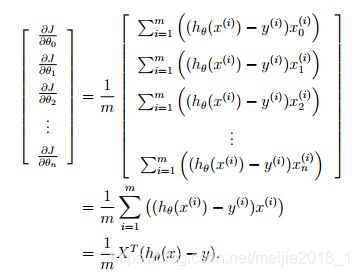
grad = X'*(sigmoid(X*theta)-y)/m;

运行程序：

Gradients:
 0.146561 
 0.051442 
 0.124722 
 0.198003 
Expected gradients:
 0.146561
 -0.548558
 0.724722
 1.398003

可以看到grad(1)与期望值一致，其余不同，这是由于未进行正则化导致的，给出的期望值是正则化后的值。
（3）矢量化正则化logistic regression
正则化有：


修改代码为：

J = (y'*log(sigmoid(X*theta))+(1-y)'*log(1-sigmoid(X*theta)))/(-m)...
    +(theta'*theta-theta(1)^2)*lambda/(2*m);
grad = X'*(sigmoid(X*theta)-y)/m+ lambda*theta/m;
grad(1) = X(:,1)'*(sigmoid(X*theta)-y)/m;

再次运行程序，得到的结果为：

Testing lrCostFunction() with regularization
Cost: 2.534819
Expected cost: 2.534819
Gradients:
 0.146561 
 -0.548558 
 0.724722 
 1.398003 
Expected gradients:
 0.146561
 -0.548558
 0.724722
 1.398003

4、多分类器
函数[all_theta] = oneVsAll(X, y, num_labels, lambda)是训练多个logistic regression分类器，其返回值all_theta为K×(N+1)矩阵，其中K为分类器的数量，N为每个样本特征值的数量。则返回值all_theta的每一行均代表的是对应的分类器（如本例中分类器label为1-10）的拟合theta值。
在编写程序时，针对训练的分类器k（k∈{1,2,…,K}），需要一个标签矢量y（此处的y并非实例中的y∈{1,2,…,10}，而是y∈{0,1}），该标签矢量需要重新通过逻辑运算获得，例如当前样本的标签矢量为[1 2 1 3 2 4]，需要训练分类器y=1，则此时输入训练的标签矢量y=[1 0 1 0 0 0]，需要训练分类器y=2，则此时输入训练的标签矢量y = [0 1 0 0 1 0]，需要训练分类器y=3，则此时输入训练的标签矢量y = [0 0 0 1 0 0]，依次类推。

function [all_theta] = oneVsAll(X, y, num_labels, lambda)
m = size(X, 1);%m行
n = size(X, 2);%n列
all_theta = zeros(num_labels, n + 1);

% Add ones to the X data matrix
X = [ones(m, 1) X];
initial_theta = zeros(n + 1, 1);  
options = optimset('GradObj', 'on', 'MaxIter', 50);
for i = 1:num_labels
    [theta] = fmincg (@(t)(lrCostFunction(t, X, (y == i), lambda)),...
        initial_theta, options);
    all_theta(i,:) = theta;
end

5、多分类器训练预测
完善predictOneVsAll函数

A = sigmoid(X*all_theta');
[max_A,p] = max(A, [], 2);

回顾之前的内容：
矩阵X每一行均代表一个样本，列为其对应样本的特征参数，本例中有5000个样本，400个特征参数，故X的维度为5000×401，其中第一列全为1，为特征参数x0,。
矩阵all_theta每一行为对应的y的label训练出来的theta值，如第1行为y=0对应的theta值，第3行为y=3对应的theta值，则在本例中all_theta的维度为10401。
通过以上分析可知sigmoid(Xall_theta’)实际上得到的是：每行为每个对应label的概率，如第1行为第一个样本计算出来的y=1-10的概率。第3行第4列的数据为第3个样本label y=4的概率。
故需要获得矩阵A = sigmoid(X*all_theta’)按行的最大值位置，即为该系统分类的对应样本的label值。
[max_A,p] = max(A, [], 2)可以完成上述工作，max_A为按行获取的最大值，p为按行获取最大值的位置。
执行程序有：

Training Set Accuracy: 94.960000