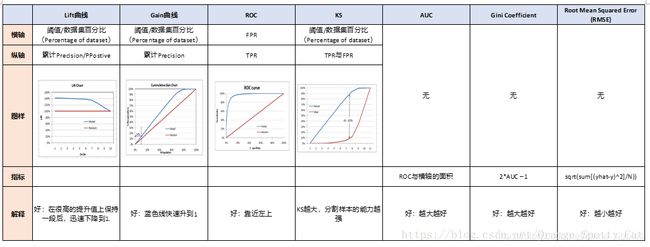
AUC、KS评价指标、洛伦兹曲线、Gini系数、Lift曲线和Gain曲线
文章目录
-
-
- 1.AUC
-
- 1.1.混淆矩阵
- 1.2.ROC曲线
- 1.3.关于AUC值
- 2.KS评价指标
- 3.洛伦兹曲线
- 4.Gini系数
- 5.Lift曲线和Gain曲线
-
- 5.1.Lift曲线
- 5.2.Gain曲线
- 6.总结
- 7.参考资料
-
关于AUC、KS评价指标、洛伦兹曲线、Gini系数、Lift曲线和Gain曲线。在别人的博客里看到下面的一个小故事:
故事是这样的:
首先,混淆矩阵是个元老,年龄最大也资历最老。创建了两个帮派,一个夫妻帮,一个阶级帮。
之后,夫妻帮里面是夫妻两个,一个Lift曲线,一个Gain曲线,两个人不分高低,共用一个横轴。
再次,阶级帮里面就比较混乱。
1.帮主是ROC曲线。
2.副帮主是KS曲线,AUC面积。
3.AUC养了一个小弟,叫GINI系数。
1.AUC
AUC为ROC曲线下的面积,用于作为二分类模型的评价指标。
要理解AUC,首先得明白混淆矩阵。
1.1.混淆矩阵
混淆矩阵如下:
| 真 | 实 | ||
|---|---|---|---|
| 1(真) | 0(假) | ||
| 预 | 1(阳) | TP(真阳) | FP(伪阳) |
| 测 | 0(阴) | FN(伪阴) | TN(真阴) |
真阳率(召回率) T P R = T P T P + F N TPR=\frac{TP}{TP+FN} TPR=TP+FNTP,表示的是,所有真实类别为1的样本中,预测类别为1的比例。TPR越大,表示越有可能是对的。
伪阳率 F P R = F P F P + T N FPR=\frac{FP}{FP+TN} FPR=FP+TNFP,表示的是,所有真实类别为0的样本中,预测类别为1的比例。
1.2.ROC曲线
横轴为FPR,纵轴为TPR。目的是希望FPR尽可能小,TPR尽可能大。
画出来的图一般如下图所示:
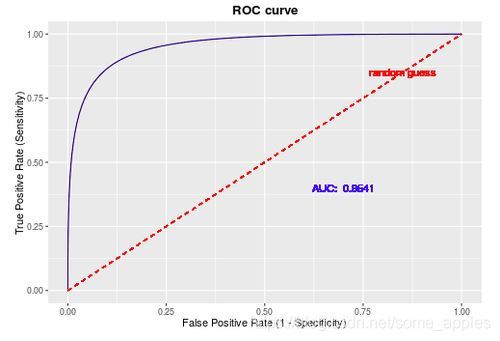
通过模型预测得到各样本的预测值(如0.6、0.7等),则通过选择归于正类的阈值来判断各个样本的类别,之后则可以计算对应的TPR和FPR。常常将得到的各个样本值对应的预测值作为阈值,并计算对应的TPR和FPR。之后将得到的各点与(0,0)和(1,1)相连,则得到了ROC曲线。之后,计算ROC曲线下的面积则有AUC值。
1.3.关于AUC值
AUC值在[0.5,1]中,0.5代表模型并无分类效果。若小于0.5则表示还不如随机猜测,但是此时如若反向预测,则得到的模型优于随机猜测。AUC值越高越好。
此外,AUC值相比于准确率这一指标好的优势在于对数据不平衡的数据集构建的模型有更好的评价意义。
例:在反欺诈场景中,0占99.9%,1占0.1%。若此时有个模型将样本全预测为0,则准确率为99.9%。虽然看起来拥有很高的准确率,但全预测为0无异于瞎猜,这样的模型并没有实际的区分能力。而当我们计算这个模型的AUC值时,就会发现,该模型的AUC值为0.5,表示并没有分类能力。这就是AUC的优势
2.KS评价指标
通过衡量好坏样本的累计分布的差值来评估模型的风险区分能力。
定义: K S = M A X ( T P R − F P R ) KS=MAX(TPR-FPR) KS=MAX(TPR−FPR)
KS与AUC均使用TPR、FPR两个指标,区别在于:
-
KS取的是TPR与FPR的差的max,可通过此找到最优阈值;
-
AUC评价的是模型整体的效果,并没给出好的切分阈值。
得到KS曲线如下图所示:
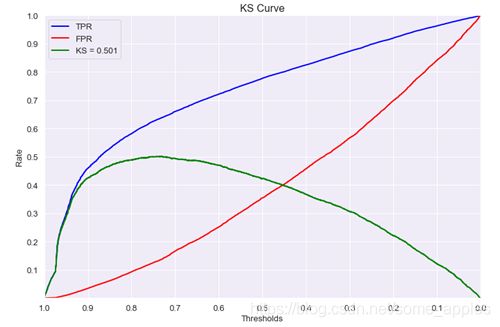
前期TPR提升越快,模型效果越好。KS取值范围 模型效果 KS<0.2 无区分能力 0.2≤KS<0.3 模型具有一定区分能力,勉强可以接受 0.3≤KS<0.5 模型有较强区分能力 0.5≤KS<0.75 模型具有很强区分能力 0.75≤KS 模型可能有异常(效果太好,以至于可能有问题)
3.洛伦兹曲线
曲线纵轴:违约数占违约总量百分比的累计值,即TPR。
曲线横轴:被拒绝申请的百分比, F P + T P F P + T N + F N + T P \frac{FP+TP}{FP+TN+FN+TP} FP+TN+FN+TPFP+TP。可理解为选择的阈值。
画出来的可能的图为:
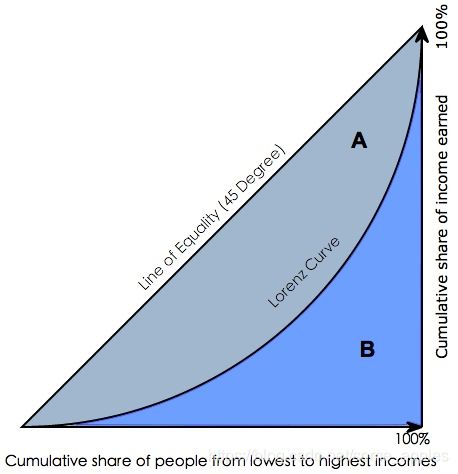 或者
或者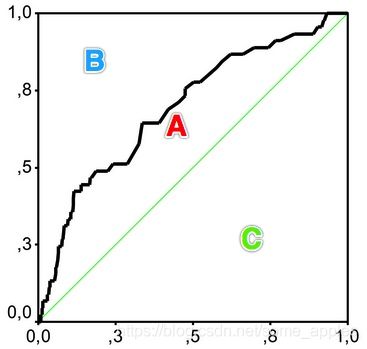
当情况中坏样本很少时,即TP与FN均较小时,有下式:
F P + T P F P + T N + F N + T P ≈ F P F P + T N \frac{FP+TP}{FP+TN+FN+TP}\approx\frac{FP}{FP+TN} FP+TN+FN+TPFP+TP≈FP+TNFP,右边即为FPR
此时,洛伦兹曲线与ROC曲线基本一致。
4.Gini系数
衡量坏账户数在好账户数上的累积分布与随机分布曲线之间的面积。
定义:绝对公平线(y=x)与洛伦兹曲线围成的面积与绝对公平线以下面积的比例。
若为上方的左图情况,则对应的 G i n i = A A + B Gini=\frac{A}{A+B} Gini=A+BA
若为上方的右图情况,则对应的 G i n i = A C = A A + B Gini=\frac{A}{C}=\frac{A}{A+B} Gini=CA=A+BA
当洛伦兹曲线与ROC曲线重合或近似一致时,此时画出来的图类似于上方右图,
有 G i n i = A A + B = A U C − C 0.5 = A U C − 0.5 0.5 Gini=\frac{A}{A+B}=\frac{AUC-C}{0.5}=\frac{AUC-0.5}{0.5} Gini=A+BA=0.5AUC−C=0.5AUC−0.5
⇒ G i n i = 2 ∗ A U C − 1 \Rightarrow Gini=2*AUC-1 ⇒Gini=2∗AUC−1
需要注意的是,此时洛伦兹曲线与ROC曲线重合或者近似一致时才成立。若因实际情况中坏样本较多,导致洛伦兹曲线与ROC曲线并不近似,则需按上方所述定义计算Gini系数。
5.Lift曲线和Gain曲线
5.1.Lift曲线
Lift曲线表示的是相较于不利用模型时模型的提升指数。衡量的是一个模型(或规则)对目标中“响应”的预测能力优于随机选择的倍数,以1为界线,大于1的Lift表示该模型或规则比随机选择捕捉了更多的“响应”。
L i f t = T P T P + F P T P + F N T P + F P + F N + T N = T P T P + F P P P + N Lift=\frac{\frac{TP}{TP+FP}}{\frac{TP+FN}{TP+FP+FN+TN}}=\frac{\frac{TP}{TP+FP}}{\frac{P}{P+N}} Lift=TP+FP+FN+TNTP+FNTP+FPTP=P+NPTP+FPTP
其中,分母表示的是不使用任何模型;分子则表示的是预测为正例的样本中的真实正例的比例。
例如(此处是对上方求解lift的式子进行解释):
若经验告诉我们10000个借款人中有1000个是逾期的,则我们向这10000个借款人借款的逾期率是10%。P / (P + N) = 10%。通过对这10000个借款人进行研究,建立模型进行分类,我们得到预计可能逾期的1000个借款人,TP + FP = 1000。但此时这1000个借款人中有300个是真的逾期了的,TP = 300,则此时的命中率TP / (TP + FP)为30%。
此时,我们的提升值lift = 30% / 10% = 3,模型找到逾期人员的效果提升至原先(无模型)的三倍。
再例如(此处是对参考资料[1]中通过贝叶斯推导得到的lift的式子进行解释):
以信用评分卡模型的评分结果为例,通常会将打分后的样本按分数从低到高排序(这句与“预测为正例的样本从大到小排序”、“预测为负例的样本从小到大排序”含义相同),取10等分或20等分或 x 等分(有同分数对应多条观测的情况,所以各组观测数未必完全相等),并对组内观测数与坏样本数进行统计。
用评分卡模型捕捉到的坏客户的占比,可由该组坏样本数除以总的坏样本数计算得出;而不使用此评分卡,以随机选择的方法覆盖到的坏客户占比,等价于该组观测数占总观测数的比例。对两者取累计值,取其比值,则得到提升度Lift,即该评分卡抓取坏客户的能力是随机选择的多少倍。
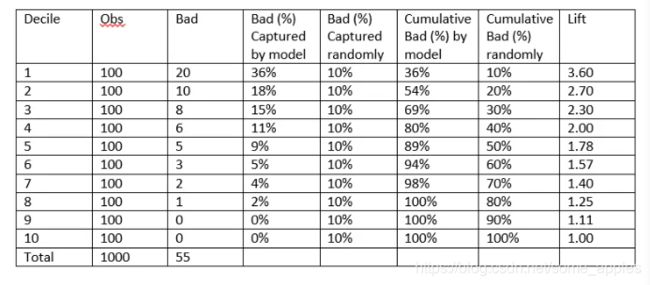
下表是一个提升表(Lift Table)的示例(对应上方的第二个例如):
注意lift是由倒数第三列 / 倒数第二列得到,原因是在每个十分位数描点时,对于lift来说,需要计算的是小于等于这个十分位数时的情况。
比如第一行,此时将0.1作为随机判断的阈值,则对于随机判断,判断得到坏样本的比例则为10%,对于模型,则判断得到坏样本的比例占比为20 / 55 = 36%;
对于第二行,此时将0.2作为随机判断的阈值,则对于随机判断,判断得到坏样本的比例则为20%,对于模型,则判断得到坏样本的比例占比为(20 + 10) / 55 = 54%,以此类推。
以分数段(此处为各个十分位数)为横轴,以提升度为纵轴,可绘制出提升图,示例如下:
Lift曲线图,当在很高的提升值上保持一段后,迅速下降至1时,表示模型较好。(为什么呢?)
(我觉得是这样的。以上方所述信用评分卡模型(假设评分卡得分为300-900)代入,这种情况表明,在前一部分(用户信用评分较低时,比如300-550)时,提升值较高则表示模型比之于无模型的时候有更好的效果。而如若一旦过了某个点(比如600),迅速下降到1,则表明该阈值下有无模型差别不大了。因此当模型有这种情况时,模型较好。优点总结为:
- 迅速下降的位置可以指导我们选择作为是否放贷的标准;
- 在信用评分较低的区间这一段保持较高的提升值,说明,在信用评分较低的区间,模型能够比无模型更能找出不良用户,且提升值还不错。)
5.2.Gain曲线
Gain曲线是整体精准度的指标。
G a i n = T P T P + F P Gain=\frac{TP}{TP+FP} Gain=TP+FPTP
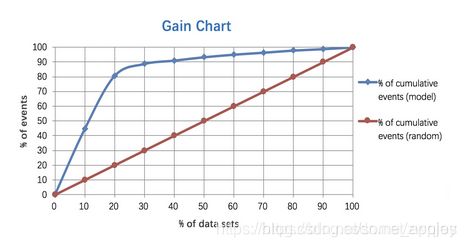
根据预测为正例的样本从大到小排序,依次选取截断点,计算Gain后绘图。(横轴为阈值)绘制出来的曲线图如下所示:
Gain曲线图,当蓝线快速上升至1时,表示模型较好。
6.总结
7.参考资料
[1] https://www.cnblogs.com/dataxon/p/12538524.html#gainlift-chart
[2] https://www.jianshu.com/p/ff0eb70d31ec
[3] https://blog.csdn.net/Orange_Spotty_Cat/article/details/82425113
以上只是自己查阅网上资料所作的学习总结,如若有说得不好的地方,也欢迎留言友善讨论。谢谢