吴恩达机器学习课程-作业8-异常检测和推荐系统(python实现)
Machine Learning(Andrew) ex8-Anomaly Detection and Recommender Systems
椰汁笔记
Anomaly detection
这是也是一个非监督学习算法
- 异常检测做什么?
从一组数据中找到那些“异常”的数据,基于高斯分布(正太分布)。生活中的很多事情都是符合高斯分布的,对于数据也是如此。我们通过参数估计,估计出数据符合的高斯分布参数,当其中的数据分布在高斯分布中概率很小的地方,就认为这是异常数据。 - 具体怎么做?
选择可以描述异常状态的特征作为输入
x ( 1 ) , x ( 2 ) , … , x ( m ) x^{(1)},x^{(2)},\dots,x^{(m)} x(1),x(2),…,x(m)
根据以往的数据估计高斯分布的参数(对每一个特征)
μ j = 1 m ∑ i = 0 m x j ( i ) σ j 2 = 1 m ∑ i = 0 m ( x j ( i ) − μ j ) 2 \mu_j=\frac{1}{m}\sum_{i=0}^{m}x_j^{(i)} \\\sigma_j^2=\frac{1}{m}\sum_{i=0}^{m}(x_j^{(i)}-\mu_j)^2 μj=m1i=0∑mxj(i)σj2=m1i=0∑m(xj(i)−μj)2
对于一个新的数据,预测其发生概率
P ( x ) = ∏ j = 1 n P ( x j ; μ j ; σ j 2 ) = ∏ j = 1 n 1 2 π σ j e − ( x j − μ ) 2 j 2 σ j 2 P(x)=\prod_{j=1}^nP(x_j;\mu_j;\sigma_j^2)=\prod_{j=1}^n\frac{1}{\sqrt{2\pi}\sigma_j}e^{-\frac{(x_j-\mu_)^2j}{2\sigma_j^2}} P(x)=j=1∏nP(xj;μj;σj2)=j=1∏n2πσj1e−2σj2(xj−μ)2j
当概率小于一定阈值后认定为异常。 - 这个算法有什么缺点?
可以看到,之前的模型中对每个特征都是独立地处理,最后的组合只是简单的相乘。这样就是存在一些问题,特征之间的关联没有捕捉到。
升级的方式就是多元高斯分布,将不再单独考虑特征,而是将特征一起考虑,自动捕捉之间的关联。
参数的估计变为,其中的sigma为协方差矩阵
μ = 1 m ∑ i = 1 m x ( i ) Σ = 1 m ∑ i = 1 m ( x ( i ) − μ ) ( x ( i ) − μ ) T \mu=\frac{1}{m}\sum_{i=1}^{m}x^{(i)} \\\Sigma=\frac{1}{m}\sum_{i=1}^{m}(x^{(i)}-\mu)(x^{(i)}-\mu)^T μ=m1i=1∑mx(i)Σ=m1i=1∑m(x(i)−μ)(x(i)−μ)T
预测变为
P ( x ; μ ; Σ ) = 1 ( 2 π ) n 2 ∣ Σ ∣ 1 2 e − 1 2 ( x − μ ) T Σ − 1 ( x − μ ) P(x;\mu;\Sigma)=\frac{1}{(2\pi)^{\frac{n}{2}}|\Sigma|^{\frac{1}{2}}}e^{-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)} P(x;μ;Σ)=(2π)2n∣Σ∣211e−21(x−μ)TΣ−1(x−μ)
这个模型有个前提就是m>n,而且协方差矩阵是非奇异矩阵。另外这个计算也是复杂的。 - 怎么评估算法的效果?
使用标签化的数据,计算F1score - 怎么感觉异常检测可以用监督学习做呢?
总结一下异常检测和监督学习的适合场景- 异常检测
(1)异常数据很少,y=1的数据很少
(2)正常数据很多,y=0的数据很多
(3)异常的类型太多
(4)未来异常的类型是未知的
典型应用:欺骗检测,监测机器 - 监督学习
(1)y=0和y=1的数据都很多
(2)异常的例子够多,且未来的异常与以往相同
典型应用:垃圾邮件分类,天气预测
- 异常检测
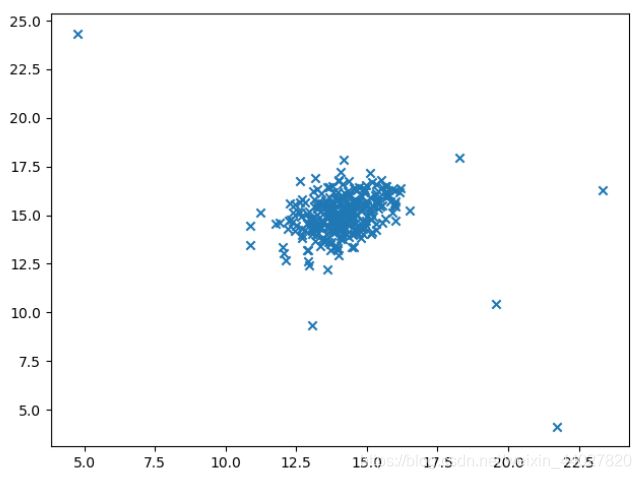
下面进行作业,先可视化数据
data = sio.loadmat("data\\ex8data1.mat")
X = data['X'] # (307,2)
plt.scatter(X[..., 0], X[..., 1], marker='x', label='point')
plt.show()
- 1.1 Gaussian distribution
假设我们已经知道了高斯模型的参数,计算概率
def gaussian_distribution(X, mu, sigma2):
"""
根据高斯模型参数,计算概率
:param X: ndarray,数据
:param mu: ndarray,均值
:param sigma2: ndarray,方差
:return: ndarray,概率
"""
p = (1 / np.sqrt(2 * np.pi * sigma2)) * np.exp(-(X - mu) ** 2 / (2 * sigma2))
return np.prod(p, axis=1) # 横向累乘
- 1.2 Estimating parameters for a Gaussian
根据数据估计出模型的参数
def estimate_parameters_for_gaussian_distribution(X):
"""
估计数据估计参数
:param X: ndarray,数据
:return: (ndarray,ndarray),均值和方差
"""
mu = np.mean(X, axis=0) # 计算方向因该是沿着0,遍历每组数据
sigma2 = np.var(X, axis=0) # N-ddof为除数,ddof默认为0
return mu, sigma2
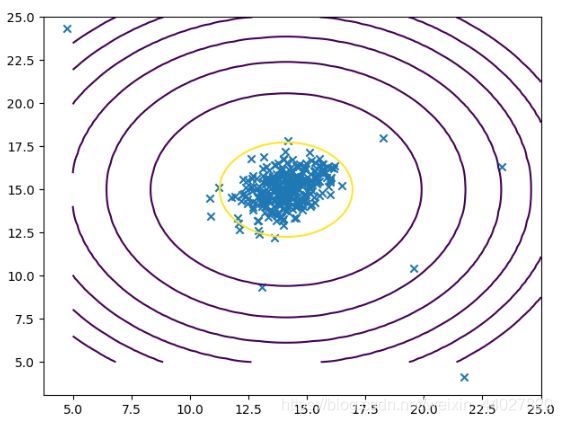
根据估计出的参数,画出高斯分布的等高线
def visualize_contours(mu, sigma2):
"""
画出高斯分布的等高线
:param mu: ndarray,均值
:param sigma2: ndarray,方差
:return: None
"""
x = np.linspace(5, 25, 100)
y = np.linspace(5, 25, 100)
xx, yy = np.meshgrid(x, y)
X = np.concatenate((xx.reshape(-1, 1), yy.reshape(-1, 1)), axis=1)
z = gaussian_distribution(X, mu, sigma2).reshape(xx.shape)
cont_levels = [10 ** h for h in range(-20, 0, 3)] # 当z为当前列表的值时才绘出等高线
plt.contour(xx, yy, z, cont_levels)
mu, sigma2 = estimate_parameters_for_gaussian_distribution(X)
p = gaussian_distribution(X, mu, sigma2)
visualize_contours(mu, sigma2)
- 1.3 Selecting the threshold, ε
要判断出是否为异常,需要一个阈值。可以通过取不同的阈值,计算标签数据的F1score等量化的评价的标准,选取最好的阈值。
首先需要对模型计算出的结果,进行误差分析,计算F1-score。这里需要注意,F1-score,precision和recall的计算,需要判断分母为0的情况。
def error_analysis(yp, yt):
"""
计算误差分析值F1-score
:param yp: ndarray,预测值
:param yt: ndarray,实际值
:return: float,F1-score
"""
tp, fp, fn, tn = 0, 0, 0, 0
for i in range(len(yp)):
if yp[i] == yt[i]:
if yp[i] == 1:
tp += 1
else:
tn += 1
else:
if yp[i] == 1:
fp += 1
else:
fn += 1
precision = tp / (tp + fp) if tp + fp else 0 # 防止除以0
recall = tp / (tp + fn) if tp + fn else 0
f1 = 2 * precision * recall / (precision + recall) if precision + recall else 0
return f1
封装阈值选择函数,阈值从预测值的最小到最大的范围中遍历,计算F1-score选择出最好的阈值选择
def select_threshold(yval, pval):
"""
根据预测值和真实值确定最好的阈值
:param yval: ndarray,真实值(这里是0或1)
:param pval: ndarray,预测值(这里是[0,1]的概率)
:return: (float,float),阈值和F1-score
"""
epsilons = np.linspace(min(pval), max(pval), 1000)
l = np.zeros((1, 2))
for e in epsilons:
ypre = (pval < e).astype(float)
f1 = error_analysis(ypre, yval)
l = np.concatenate((l, np.array([[e, f1]])), axis=0)
index = np.argmax(l[..., 1])
return l[index, 0], l[index, 1]
测试
Xval = data['Xval'] # (307,2)
yval = data['yval'] # (307,1)
e, f1 = select_threshold(yval.ravel(), gaussian_distribution(Xval, mu, sigma2))
print('best choice of epsilon is ', e, ',the F1 score is ', f1)
# best choice of epsilon is 8.999852631901393e-05 ,the F1 score is 0.8750000000000001
利用选择出来的阈值完善模型,对异常进行预测。
def detection(X, e, mu, sigma2):
"""
根据高斯模型检测出异常数据
:param X: ndarray,需要检查的数据
:param e: float,阈值
:param mu: ndarray,均值
:param sigma2: ndarray,方差
:return: ndarray,异常数据
"""
p = gaussian_distribution(X, mu, sigma2)
anomaly_points = np.array([X[i] for i in range(len(p)) if p[i] < e])
return anomaly_points
我们将异常的数据点圈出来
def visualize_dataset(X):
plt.scatter(X[..., 0], X[..., 1], marker='x', label='point')
def circle_anomaly_points(X):
plt.scatter(X[..., 0], X[..., 1], s=80, facecolors='none', edgecolors='r', label='anomaly point')
anomaly_points = detection(X, e, mu, sigma2)
circle_anomaly_points(anomaly_points)
plt.title('anomaly detection')
plt.legend()
plt.show()
- 1.4 High dimensional dataset
异常检测的方法都写好了,对于高维的数据,也是一样的操作就行
data2 = sio.loadmat("data\\ex8data2.mat")
X = data2['X']
Xval = data2['Xval']
yval = data2['yval']
mu, sigma2 = estimate_parameters_for_gaussian_distribution(X)
e, f1 = select_threshold(yval.ravel(), gaussian_distribution(Xval, mu, sigma2))
anomaly_points = detection(X, e, mu, sigma2)
print('\n\nfor this high dimensional dataset \nbest choice of epsilon is ', e, ',the F1 score is ', f1)
print('the number of anomaly points is', anomaly_points.shape[0])
# for this high dimensional dataset
# best choice of epsilon is 1.3786074982000235e-18 ,the F1 score is 0.6153846153846154
# the number of anomaly points is 117
Recommender Systems
拿电影网站来说,通常我们都会给自己看过的电影评分,作为网站运营者要进行其他电影的推荐,那么就需要根据你之前的评分。
假设我们对每个电影给出一个向量x代表一系列特征,那么根据用户对部分电影的评分,我们可以使用线性回归的方式求出一个向量theta这个向量代表用户的一系列特征,那么我们就可以通过计算theta^T·x得到对于用户未评分电影的预测评分,就可以通过这个进行推荐。
从令一个角度看,假设我们对每个用户给出一个向量theta,与上面相同的方法,也可以求出电影的特征向量x,同样进行电影评分预测。
但是不管是用户特征还是电影特征都难以手动确定,那怎么实现推荐系统呢?
协同过滤算法
现实情况是我们都不知道用户特征和电影特征,只知道用户对哪些电影评分,评分的分数。协同过滤算法的思路是我们直接一起训练用户特征和电影特征,首先随机初始化用户特征和电影特征,在每一次梯度下降过程中,先后更新用户特征和电影特征,最后就能得到用户特征和电影特征并进行预测。
为什么可以先后跟新用户特征和电影特征呢?因为他们的优化目标函数是相同的。
J ( x ( 1 ) , … , x ( n m ) ; θ ( 1 ) , … , θ ( n u ) ) = 1 2 ∑ ( i , j ) : r ( i , j ) = 1 ( ( θ ( j ) ) T x ( i ) − y ( i , j ) ) 2 + λ 2 ∑ i = 1 n m ∑ k = 1 n ( x k ( i ) ) 2 + λ 2 ∑ j = 1 n u ∑ k = 1 n ( θ k ( j ) ) 2 J(x^{(1)},\dots,x^{(n_m)};\theta^{(1)},\dots,\theta^{(n_u)})=\frac{1}{2}\sum_{(i,j):r(i,j)=1}((\theta^{(j)})^Tx^{(i)}-y^{(i,j)})^2+\frac{\lambda}{2}\sum_{i=1}^{n_m}\sum{k=1}{n}(x_k^{(i)})^2+\frac{\lambda}{2}\sum_{j=1}^{n_u}\sum{k=1}{n}(\theta_k^{(j)})^2 J(x(1),…,x(nm);θ(1),…,θ(nu))=21(i,j):r(i,j)=1∑((θ(j))Tx(i)−y(i,j))2+2λi=1∑nm∑k=1n(xk(i))2+2λj=1∑nu∑k=1n(θk(j))2
只需要保证用户特征和电影特征的特征数量是相同的即可
具体的算法流程是:
1.随机初始化用户特征theta和电影特征x,这里需要保证两个维度一样
2.使用梯度下降或其他优化算法更新两个特征参数
x k ( i ) = x k ( i ) − α ( ∑ ( i , j ) : r ( i , j ) = 1 ( ( θ ( j ) ) T x ( i ) − y ( i , j ) ) θ k ( j ) + λ x k ( i ) ) θ k ( j ) = θ k ( j ) − α ( ∑ ( i , j ) : r ( i , j ) = 1 ( ( θ ( j ) ) T x ( i ) − y ( i , j ) ) x k ( i ) + λ θ k ( j ) ) x_k^{(i)}=x_k^{(i)}-\alpha(\sum_{(i,j):r(i,j)=1}((\theta^{(j)})^Tx^{(i)}-y^{(i,j)})\theta_k^{(j)}+\lambda x_k^{(i)}) \\\theta_k^{(j)}=\theta_k^{(j)}-\alpha(\sum_{(i,j):r(i,j)=1}((\theta^{(j)})^Tx^{(i)}-y^{(i,j)})x_k^{(i)}+\lambda \theta_k^{(j)}) xk(i)=xk(i)−α((i,j):r(i,j)=1∑((θ(j))Tx(i)−y(i,j))θk(j)+λxk(i))θk(j)=θk(j)−α((i,j):r(i,j)=1∑((θ(j))Tx(i)−y(i,j))xk(i)+λθk(j))
3.用着两个特征预测评分,进行排序推荐
p r e d i c t = θ T x predict=\theta^Tx predict=θTx
- 2.2.1 Collaborative filtering cost function
实现目标函数,参数应该是一维向量,需要将用户特征和电影特征一维序列化,在计算损失值内部还原为原来的形式
def serialize(X, theta):
"""
参数一维向量化
:param X: ndarray,电影特征
:param theta: ndarray,用户特征
:return: ndarray,一维化向量
"""
return np.concatenate((X.flatten(), theta.flatten()), axis=0)
def deserialize(params, nm, nu, nf):
"""
将一维化参数向量还原
:param params: ndarray,一维化的用户特征和电影特征
:param nm: int,电影数量
:param nu: int,用户数量
:param nf: int,特征数量
:return: (ndarray,ndarray) 电影特征,用户特征
"""
X = params[:nm * nf].reshape(nm, nf)
theta = params[nm * nf:].reshape(nu, nf)
return X, theta
然后我们再来实现损失值计算,这里直接将正则化项加入。这里与线性回归不同的地方就是不用添加x0和theta0,正则化项里面就不需要去掉0项
def collaborative_filtering_cost(params, Y, R, nm, nu, nf, l=0.0):
"""
协同过滤算法目标函数
:param params: ndarray,一维化的用户特征和电影特征
:param Y: ndarray,表明用户的评分
:param R: ndarray,表明哪些用户评价了哪些电影
:param nm: int,电影数量
:param nu: int,用户数量
:param nf: int,特征数量
:param l: float,惩罚参数
:return: float,损失值
"""
X, theta = deserialize(params, nm, nu, nf)
part1 = np.sum(((X.dot(theta.T) - Y) ** 2) * R) / 2
part2 = l * np.sum(theta ** 2) / 2
part3 = l * np.sum(X ** 2) / 2
return part1 + part2 + part3
测试不带正则化项时,直接将参数赋为 0
data1 = sio.loadmat("data\\ex8_movies.mat")
Y = data1["Y"] # (1682,943)
R = data1["R"] # (1682,943)
data2 = sio.loadmat("data\\ex8_movieParams.mat")
X = data2["X"] # (1682,10)
theta = data2["Theta"] # (943,10)
nu = data2["num_users"][0][0] # (1,1) 943
nm = data2["num_movies"][0][0] # (1,1) 1682
nf = data2["num_features"][0][0] # (1,1) 10
# 题目中计算数据不是全部数据,取nm=5,nu=4,nf=3,值为22.224603725685675
nu = 4
nm = 5
nf = 3
X = X[:nm, :nf]
theta = theta[:nu, :nf]
Y = Y[:nm, :nu]
R = R[:nm, :nu]
print(collaborative_filtering_cost(serialize(X, theta), Y, R, nm, nu, nf))
# 22.224603725685675
- 2.2.2 Collaborative filtering gradient
实现协同过滤梯度下降,这里也先实现正则部分
def collaborative_filtering_gradient(params, Y, R, nm, nu, nf, l=0.0):
"""
协同过滤梯度下降
:param params: ndarray,一维化的用户特征和电影特征
:param Y: ndarray,表明用户的评分
:param R: ndarray,表明哪些用户评价了哪些电影
:param nm: int,电影数量
:param nu: int,用户数量
:param nf: int,特征数量
:param l: float,惩罚参数
:return: ndarray,跟新后的一维化的用户特征和电影特征
"""
X, theta = deserialize(params, nm, nu, nf)
g_X = ((X.dot(theta.T) - Y) * R).dot(theta) + l * X
g_theta = ((X.dot(theta.T) - Y) * R).T.dot(X) + l * theta
return serialize(g_X, g_theta)
- 2.2.3 Regularized cost function
上面已经完成,直接使用,当惩罚参数为1.5时的
# 正则化时选择的lambda为1.5
print(collaborative_filtering_cost(serialize(X, theta), Y, R, nm, nu, nf, 1.5))
# 31.34405624427422
- 2.2.4 Regularized gradient
已经实现
测试需要用到梯度下降检测,就是求一个近视的导数。不知道为什么,梯度下降检测运行得太慢,没有跑出结果。
def check_gradient(params, Y, R, nm, nu, nf):
# X, theta = deserialize(params, nm, nu, nf)
e = 0.0001
m = len(params)
g_params = np.zeros((m,))
for i in range(m):
temp = np.zeros((m,))
temp[i] = e
g_params[i] = (collaborative_filtering_cost(params + temp, Y, R, nm, nu, nf) -
collaborative_filtering_cost(params - temp, Y, R, nm, nu, nf)) / (2 * e)
return g_params
- 2.3 Learning movie recommendations
这里训练模型,首先添加自定义数据
# 先添加一组自定义的用户数据
my_ratings = np.zeros((1682, 1))
my_ratings[0] = 4
my_ratings[97] = 2
my_ratings[6] = 3
my_ratings[11] = 5
my_ratings[53] = 4
my_ratings[63] = 5
my_ratings[65] = 3
my_ratings[68] = 5
my_ratings[182] = 4
my_ratings[225] = 5
my_ratings[354] = 5
Y = np.concatenate((Y, my_ratings), axis=1)
R = np.concatenate((R, my_ratings > 0), axis=1)
nu += 1
利用scipy.optimize.minimize()的高级优化方法去做
params = serialize(np.random.random((nm, nf)), np.random.random((nu, nf)))
res = opt.minimize(fun=collaborative_filtering_cost, x0=params, args=(Y, R, nm, nu, nf, 10),
method='TNC',
jac=collaborative_filtering_gradient)
利用优化后的参数进行预测
trained_X, trained_theta = deserialize(res.x, nm, nu, nf)
predict = trained_X.dot(trained_theta.T)
my_predict = predict[..., -1]
选出十个最高的评分,显示推荐结果。我们还要读入电影名。
# 读入电影标签
f = open("data\\movie_ids.txt", "r")
movies = []
for line in f.readlines():
movies.append(line.split(' ', 1)[-1][:-1])
# 先打印构造的用户数据
for i in range(len(my_ratings)):
if my_ratings[i] > 0:
print(my_ratings[i], movies[i])
# 从预测结果中选10个最优推荐
# 由于训练初始化参数的不同会导致最后的结果不同
print("Top recommendations for you:")
for i in range(10):
index = int(np.argmax(my_predict))
print("Predicting rating ", my_predict[index], " for movie ", movies[index])
my_predict[index] = -1

由于初始化参数的问题,推荐的结果可能出现差异。我们用可量化的评价方法进行评价看看模型的误差怎么样就行了。这里的评价是将预测和实际评分计算方差,未评分的不计算。可以看到还是不错
# 用均方误差来评价
Y = Y.flatten()
R = R.flatten()
predict = predict.flatten()
true_y = []
pre_y = []
for i in range(len(Y)):
if R[i] == 1:
true_y.append(Y[i])
pre_y.append(predict[i])
print("当前训练对岳原始数据集的均方误差", mean_squared_error(true_y, pre_y))
# 当前训练对岳原始数据集的均方误差 0.6400023155268085
另外当用户没有任何评分记录时,学习结果将会是theta为0.为了避免所有都是0,导致计算出的所有预测评分都是0,我们可以先将评分数据减去均值。最后预测再加上。
最后在再记录一下,后面课程学习的内容
随机梯度下降
之前我们使用的都是批量梯度下降,每次迭代需要遍历所有数据。在现在,为了使算法更加的好,通常都会使用大量的数据去训练算法。随着数据量的增多,数据无法完全存储在内存中,数据读取需要到磁盘,反复读取操作将会是非常地费时。
因此随机梯度下降是个很好的选择,将数据排列顺序打乱,每次迭代只根据一组数据进行拟合。外层循环为1-10次,通常情况下只需要遍历一次数据即可
Repeat{
for i=0 to m:
θ j = θ j − α ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) (for j=0 to n) \theta_j=\theta_j-\alpha(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)}\textrm{(for j=0 to n)} θj=θj−α(hθ(x(i))−y(i))xj(i)(for j=0 to n)
}
另外还有一种叫做mini-batch gradient descent,他的想法就是每次迭代使用b个样本而不是随机梯度下降中的一个样本,这个b一般取2到100。当向量化做得好时,可以比随机梯度下降的速度更快。
Repeat{
while(i
}
}
怎么判断随机梯度下降收敛呢?
每迭代1000轮,计算最后1000个样本的平均损失值,并画出图像
这个1000的选择需要注意,如果太小图像产生很多噪声,越大图像越平滑。
同时如果学习速率不变,随机梯度下降的收敛值会在局部最小周围扰动。为了使扰动尽可能的小,可以动态改变学习速率
α = c o n s t 1 c o n s t 2 + i t e r a t i o n s \alpha=\frac{const1}{const2+iterations} α=const2+iterationsconst1
由于随机梯度下降每次只对一个数据进行拟合,我们可以用这个构建一个在线学习算法,每次到来一个数据就用随机梯度下降进行拟合这个数据。
完整的代码会同步 在我的github
欢迎指正错误