神经网络学习小记录5——利用Keras进行回归运算

学习前言

看了好多Github，用于保存模型的库都是Keras，我觉得还是好好学习一下的好。

什么是Keras

Keras是一个由Python编写的开源人工神经网络库，可以作Tensorflow、Microsoft-CNTK和Theano的高阶应用程序接口，进行深度学习模型的设计、调试、评估、应用和可视化。
Keras相当于比Tensorflow和Theano更高一层的库，其可以以Tensorflow或者Theano为底层框架，以更加简洁、高效的方式添加代码。
在2018年Tensorflow 2.0.0公开后，Keras被正式确立为Tensorflow高阶API。

Keras中基础的重要函数

1、Sequential

Sequential又称为序贯模型。
序贯模型为最简单的线性、从头到尾的结构顺序，不分叉，是多个网络层的线性堆叠。
在利用Keras进行模型构建前，只需要用如下函数建立模型就够了。

model = Sequential()

此时便已经建立了一个按次序的模型，之后在往模型中添加层的时候，就是按照次序添加的。

2、Dense

Dense用于往Sequential中添加全连接层。全连接层示意图如下。（图片源自百度百科）

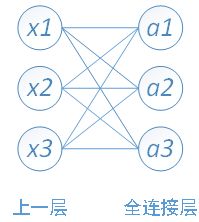
具体而言，简单的BP神经网络中，输入层到隐含层中间的权值连接，其实与全连接层的意义相同。
在Keras中，如果需要往model中添加全连接层，可使用如下函数。

model.add(Dense(output_dim = 1,input_dim = 1))

此时表示输入维度为1，输出维度也为1。

3、model.compile

model.compile在Keras中的作用主要用于定义loss函数和优化器。
其调用方式如下：

model.compile(loss='mse', optimizer='sgd', metrics=['accuracy'])

其中loss用于定义计算损失的损失函数，其可以选择的内容如下：
1、mse：均方根误差，常用于回归预测。
2、categorical_crossentropy：亦称作多类的对数损失，注意使用该目标函数时，需要将标签转化为形如(nb_samples, nb_classes)的二值序列，常用于分类。
3、sparse_categorical_crossentrop：如上，但接受稀疏标签。

optimizer用于定义优化器，可以使用默认的，也可以从keras.optimizers导出。其可以选择的内容可以参照Keras中文文档。上文中选择的是随机梯度下降法sgd。
Keras中文文档

metrics=[‘accuracy’]常用于分类运算中，本例子中不适用，accuracy代表计算分类精确度。

全部代码

该例子为一元线性回归例子。

import numpy as np
from keras.models import Sequential
from keras.layers import Dense  ## 全连接层
import matplotlib.pyplot as plt 

# 生成测试数据
X = np.linspace(-1,1,200)
np.random.shuffle(X)
Y = 0.5*X + 2 + np.random.normal(0,0.05,(200,))

# 划分训练集和测试集
X_train,Y_train = X[:160],Y[:160]
X_test,Y_test = X[160:],Y[160:]

# start
model = Sequential()
model.add(Dense(output_dim = 1,input_dim = 1))

# compile
model.compile(loss = 'mse',optimizer = 'sgd')


# 训练
print("\ntraining")
for step in range(2001):
    cost = model.train_on_batch(X_train,Y_train)
    if step%100 == 0:
        print("tarin_cost:",cost)

# 测试
print("\nTest")
cost = model.evaluate(X_test,Y_test,batch_size=40)
W,b = model.layers[0].get_weights()
print("Weights",W,"biaxes",b)

# 预测结果
Y = model.predict(X_test)
plt.scatter(X_test,Y_test)
plt.plot(X_test,Y)
plt.show()

实现结果为：

tarin_cost: 4.506874
tarin_cost: 0.21098542
tarin_cost: 0.041809298
tarin_cost: 0.013134768
tarin_cost: 0.0055761375
tarin_cost: 0.0035068158
tarin_cost: 0.0029388934
tarin_cost: 0.002783
tarin_cost: 0.0027402083
tarin_cost: 0.002728462
tarin_cost: 0.0027252387
tarin_cost: 0.0027243525
tarin_cost: 0.0027241106
tarin_cost: 0.0027240426
tarin_cost: 0.002724025
tarin_cost: 0.0027240203
tarin_cost: 0.0027240184
tarin_cost: 0.0027240182
tarin_cost: 0.0027240175
tarin_cost: 0.0027240175
tarin_cost: 0.0027240175

Test
40/40 [==============================] - 0s 874us/step
Weights [[0.5041559]] biaxes [1.9961643]

有不懂的朋友可以评论询问噢。