图与搜索 Graph&Search
图的介绍
图是节点集合的一个拓扑结构,节点之间通过边相连。图分为有向图和无向图。有向图的边具有指向性,即A-B仅表示由A到B的路径,但并不意味着B可以连到A。与之对应地,无向图的每条边都表示一条双向路径。
可称为:DAG Directed acyclic graph
图的表达方式

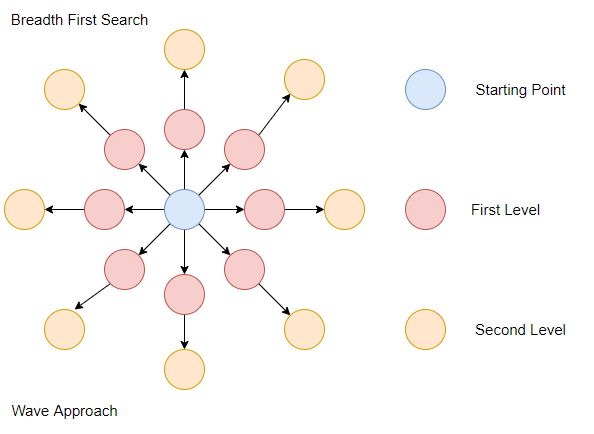
宽度优先搜索——BFS(Breadth First Search)
BFS(G, s)
For each vertex u exept s
Do Color[u] = WHITE
Distance[u] = MAX
Parent[u] = NIL
Color[s] = GRAY
Distance[s] = 0
Parent[s] = NIL
Enqueue(Q, s)
While Q not empty
Do u = Dequeue(Q)
For each v is the neighbor of u
Do if Color[v] == WHITE
Color[v] = GRAY
Distance[v] = Distance[u] + 1
Parent[v] = u
Enqueue(Q, v)
Color[u] = BLACK
BFS特点
搜索所有可以到达的状态,转移顺序为『初始状态->只需一次转移就可到达的所有状态->只需两次转移就可到达的所有状态->…』,所以对于同一个状态,BFS 只搜索一次
BFS 通常配合队列一起使用,搜索时先将状态加入到队列中,然后从队列顶端不断取出状态,再把从该状态可转移到的状态中尚未访问过的部分加入队列,知道队列为空或已找到解。因此 BFS 适合用于『由近及远』的搜索,比较适合用于求解最短路径、最少操作之类的问题。
深度优先
DFS(G)
For each vertex v in G
Do Color[v] = WHITE
Parent[v] = NIL
For each vertex v in G
DFS_Visit(v)
DFS_Visit(u)
Color[u] = GRAY
For each v is the neighbor of u
If Color[v] == WHITE
Parent[v] = u
DFS_Visit(v)
Color[u] = BLACK
回溯
DFS 通常从某个状态开始,根据特定的规则转移状态,直至无法转移(节点为空),然后回退到之前一步状态,继续按照指定规则转移状态,直⾄至遍历完所有状态
回溯法包含了多类问题,模板类似。
排列组合模板->搜索问题(是否要排序,哪些情况要跳过)
使用回溯法的一般步骤:
确定所给问题的解空间:⾸首先应明确定义问题的解空间,解空间中至少包含问题的一个解。
确定结点的扩展搜索规则以深度优先方式搜索解空间,并在搜索过程中用剪枝函数避免无效搜索。
模式识别
⽤用Backtracking( Top-Down )解决发散结构问题
对于发散性问题(例如“所有组合”,“全部解”),可以选取其问题空间“收敛”的一端作为起点,沿着节点发散的方向(或者说,当前节点的多种选择)进行递归,直到a.当前节点“不合法” 或 b.当前节点发散方向搜索完毕,才会return。
如果需要记录决策的路径,可以用vector沿着搜索的方向记录,在满足胜利条件时记录当前path(通常是将path存入vector。
Backtracking的典型模板c
void backtracking( P node, vector<P> &path, vector<vector<P> >&paths ){
if(!node ) // invalid node
return;
path.push_back(node);
bool success = ; // condition for success
if( success )
paths.push_back( vector<P>(path.begin(),path.end()) ); // don't return here
for( P next: all directions )
backtracking( next, path, paths );
path.pop_back();
return;
}
Typical Examples 典型例题
Parentheses
Given n pairs of parentheses, generate all valid combinations of parentheses.
E.g. if n = 2, you should return ()(), (())
void parenthesesCombination(int leftRem, int rightRem, string &path, vector<string> &paths)
{
if(leftRem<0 || rightRem<0)
return;;
if(leftRem>0){
//make choice
path.push_back('(');
parenthesesCombination(leftRem-1,rightRem,path,paths);
//backtracking
path.pop_back;
}
if(leftRem<rightRem){
//make choicepath.push_back(')');
rightRem -= 1;
if(rightRem == 0)
path.push_back(path); //winning
parenthesesCombination(leftRem, rightRem,path, paths);
//breaktracking
path.pop_back();
}
}
vector<string> generateParenthesis(int n){
vector<string> res;
if(n<=0)
return res;
string path;
parenthesesCombination(n,n,path,res);
return res;
}
N Queen
Please write a function to find all ways to place n queens on an n×n chessboard such that no two queens attack each other.

bool checkValid(int row1,int col1,int *rowCol){
for(int row2 = row1 - 1;row2>=0; row2--){
if(rowCol[row2[ == col1)
return false;
if(abs(row1 - row2) == abs(rowCol[row2] - col1))
return false;
}
return true;
}
void placeQ(int row,int rowCol[], vector<int*>& res){
if(row == GRID_SIZE){
//winning
int p[GRID_SIZE];
for(int i=0; i<GRID_SIZE; i++)
p[i] = rowCol[i];
res.push_back(p);
}
itn col=0;
for(col=0; col<GRID_SIZE; col++){
if(checkValid(row,col,rowCol)){
rowCol[row] = col;
placeQ(row+1, rowCol, res);
//breacuse we rewrite rowCol[row] everytime, so backtracking is inferred here
}
}
}
const int GRID_SIZE;
//OR
vector<int*>& placeQ(int N){
GRID_SIZE = N;
int [] rowCol = new int[N];
vector<int*>& res;
placeQ(0, rowCol, res);
return res;
}
部分排列
问题:从0-9这⼗十个数字中选取3个数字进⾏行排列,打印所有的组合结果。
全排列是求出了所有字母的排列方式,该题是求出了部分字母排列的⽅方法。只需要将结束的条件由if (index == size - 1)改为 if (index == m)即可,其中m是指要进行全排列的字符个数
//全排列
void Permutation(char*pStr,char*pBegin){
assert(pStr&&pBegin);
if(*pBegin=='\0')
printf("%s\n",pStr);
else{
for(char*pCh=pBegin;*pCh!='\0';pCh++){
swap(*pBegin,*pCh);
Permutation(pStr,pBegin+1);
swap(*pBegin,*pCh);
}
}
}
void swap(int&a,int&b){
int temp=a;
a=b;
b=temp;
}
//从size个字符中选取m个字符进行全排列,打印排列结果
void Permutation(char str[],int index,int m,int size){
if(index==m){
//和本文第一个程序比只是这里打印时不太相同
for(inti=0;i<m;i++)
cout << str[i];
cout <<"\t";
}else{
for(int i=index;i< size;i++){
swap(str[index],str[i]);
Permutation(str,index+1,m,size);
swap(str[index],str[il);
}
}
}
有重复的全排列
a, b, b
b, a, b
b, b, a
1.全排列就是从第一个数字起每个数分别与它后面的数字交换。
2.去重的全排列就是从第一个数字起每个数分别与它后面非重复出现的数字交换。
3.全排列的非递归就是由后向前找替换数和替换点,然后由后向前找第一个比替换数大的数与替换数交换,最后颠倒替换点后的所有数据。
//解法1:在pszStr数组中,[nBegin,nEnd)中是否有数字与下标为nEnd的数字相等
bool IsSwap(char*pszStr,int nBegin,int nEnd){
for(int i=nBegin;i< nEnd;i++)
if(pszStr[i]==pszStr[nEnd])
return false;
return true;
}
//k表示当前选取到第几个数,m表示共有多少数。
void PermutationHaveSameword(char*pszStr,int k,int m){
if(k==m){
printf("%s\n",pszStr);r
}else{
for(inti=k;i<=m;i++){
//第i个数分别与它后面的数字交换就能得到新的排列
if(IsSwap(pszStr,k,i)){
swap(pszStr[k],pszStr[il);
PermutationHaveSameword(pszStr,k+1,m);
swap(pszStr[k],pszStr[il);
}
}
}
}
void main(){
char* str="abb";
PermutationHaveSameword(str,0,strlen(str));
}
//解法2:使用set去消重
void permuteHelper(int index,vectorsint > & num,vectorsvector<int >> &paths){
if(index > num.size()){
return;
}
if(index == num.size()){
paths.push_back(num);
}
unordered_set<int> used;
for(int i = index;i < num.size();i++){
//handle duplicates
if(used.count(num[i]))
continue;
//make choice
swap(num,index,i);
permuteHelper(index+1,num,paths);
//backtracking
swap(num,index,i);
used.insert(num[i]);
}
}
void swap(vector<int>& num, int start, int end) {
int temp = num[start];
num[start] = num[end];
num[end] = temp;
}
vector<vector<int>> permuteUnique(vector<int> & num) {
vector<vector<int>> paths;
permuteHelper(0, num, paths);
return paths;
}