浅谈网络流(最大流,最小割,mcmf,最大匹配)
前言:
对于网络流的基础知识,网上许多大佬解释得很透彻了,我在这里也不去挑战大佬权威了!
这篇博客记录我一周学习网络流的学习笔记!以后还会逐渐完善!
一、最大流
最大流定理:
如果残留网络上找不到增广路径,则当前流为最大 流;反之,如果当前流不为最大流,则一定有增广路径。
用最大流的增广路经求二分图匹配:
求二分图匹配的过程就是求最大曾广路的问题,而最大流定理就是将两者之间联系起来,所以,二分图最大匹配问题用最大流做也是一个好方法。所以,用网络流在求二分图匹配时候,我们首先要做的就是求出最大流。
说到最大流,最大流求法呢也是有很多的!对比一下哈~
FF(Ford-Fulkerson)算法 :
步骤:
(1)如果存在增广路径,就找出一条增广路径 DFS(EK算法为BFS)
(2)然后沿该条增广路径进行更新流量 (增加流量)
While 有增广路径 :
do 更新该路径的流量
时间复杂度:
O(cn^2),c(边的容量和C,顶点数N)
代码:
参考https://blog.csdn.net/m0_37846371/article/details/76348989
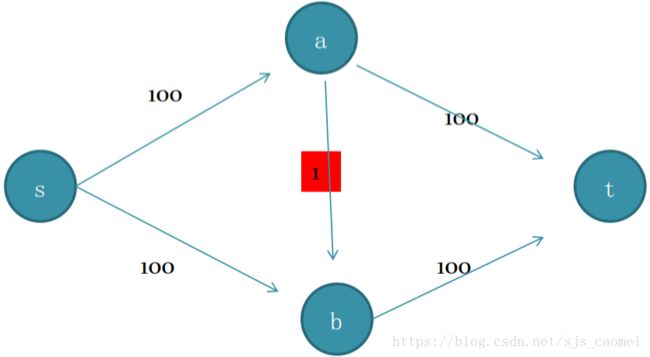
缺点:如果运气不好 这种图会让你的程序执行200次dfs 虽然实际上最少只要2次我们就能得到最大流
EK(Edmonds-Karp)算法:
步骤:
(1)如果存在增广路径,就找出一条增广路径 BFS
(2)然后沿该条增广路径进行更新流量 (增加流量)
时间复杂度:
O(nm^2)(顶点数N,边数M)
代码:
以hdu3549为例的ac代码
//O(m^2*n)
#include
using namespace std;
const int maxm=1e4+5;
const int maxn=15+5;
const int inf=0x7f7f7f7f;
struct edge
{
int next,v,w;
}edge[maxm];
int head[maxn];
int vis[maxn];//存储是否被访问
int pre[maxn];//记录前驱
int last[maxn];//记录前驱顶点和当前顶点的边的编号
int cnt;
void init()
{
cnt=0;
memset(head,-1,sizeof(head));
}
void add_edge(int u,int v,int w)
{
//正向边
edge[cnt].v=v;
edge[cnt].w=w;
edge[cnt].next=head[u],head[u]=cnt++;
//反向边
edge[cnt].v=u,edge[cnt].w=0;
edge[cnt].next=head[v],head[v]=cnt++;
}
bool bfs(int s,int e)
{
queue q;
memset(vis,0,sizeof(vis));
//memset(pre,-1,sizeof(pre));
vis[s]=1;
q.push(s);
while(!q.empty())
{
int u=q.front();
q.pop();
for(int i=head[u];i!=-1;i=edge[i].next)
{
int v=edge[i].v,w=edge[i].w;
if(!vis[v] && w)
{
last[v]=i;
pre[v]=u;
vis[v]=1;
if(v==e)
return true;
q.push(v);
}
}
}
return false;
}
int EK(int s,int e)
{
int flow=0;
while(bfs(s,e))
{
int d=inf;
/*for(int i=e;i!=s;i=pre[i])
cout<>t;
while(t--)
{
cin>>n>>m;
init();
for(int i=0;i>u>>v>>w;
add_edge(u,v,w);
}
printf("Case %d: %d\n",flag++,EK(1,n) );
}
return 0;
}
dinic算法:
这个算法是基于FF与EK的联合提出来的算法,同时用到BFS与DFS。
步骤:
(1):建造原网络G的一个分层网络L。
(2):用增广路算法计算L的最大流F,若在L中找不 到增广路,算法结束。
(3):根据F更新G中的流f,转STEP1。
分层网络的构造算法:
STEP1:标号源节点s,M[s]=0。
STEP2:调用广度优先遍历算法,执行一步遍历操作, 当前遍历的弧e=v1v2,令r=G.u(e)-G.f(e)。
若r>0,则
(1) 若M[v2]还没有遍历,则M[v2]=M[v1]+1,且将 弧e加入到L中,容量L.u(e)=r。
(2) 若M[v2]已经遍历且M[v2]=M[v1]+1,则将边e 加入到L中,容量L.u(e)=r。
(3) 否则L.u(e)=0。 否则L.u(e)=0。 重复本步直至G遍历完。其中的G.u(e)、G.f(e)、L.u(e) 分别表示图G中弧e的容量上界和当前流量,图L中弧e 的容量上界。
时间复杂度:O(mn^2)邻接表表示图,空间复杂度为O(n+m)。
又是hdu3549哈,以下是未优化以及优化过的dinic:
未优化代码:
//链式前向星dinic
//O(mn^2)
#include
using namespace std;
const int maxm=1e4+5;
const int maxn=15+5;
const int inf=0x7f7f7f7f;
struct edge
{
int next;
int v,w;
}edge[maxm];
int m,n;
int cnt,head[maxn];
int dis[maxn];
void init()
{
cnt=0;
memset(head,-1,sizeof(head));
}
void add_edge(int u,int v,int w)
{
edge[cnt].v=v,edge[cnt].w=w;
edge[cnt].next=head[u],head[u]=cnt++;
edge[cnt].v=u,edge[cnt].w=0;
edge[cnt].next=head[v],head[v]=cnt++;
}
//分层
bool bfs()
{
memset(dis,-1,sizeof(dis));
queue q;
dis[1]=0;
q.push(1);
while(!q.empty())
{
int u=q.front();
q.pop();
if(u==n)
return true;
for(int i=head[u];~i;i=edge[i].next)
{
int v=edge[i].v,w=edge[i].w;
if(dis[v]==-1 && w)
{
dis[v]=dis[u]+1;
q.push(v);
}
}
}
return false;
}
//求增广路
int dfs(int s,int t,int flow)
{
if(s==t)
return flow;
int pre=0;
for(int i=head[s];~i;i=edge[i].next)
{
int v=edge[i].v,w=edge[i].w;
if(dis[s]+1==dis[v] && w>0)
{
int tmp=min(flow-pre,w);
int tf=dfs(v,t,tmp);
edge[i].w-=tf;
edge[i^1].w+=tf;
pre+=tf;
if(pre==flow)
return pre;
}
}
return pre;
}
int dinic()
{
int ret = 0;
while(bfs())
ret+=dfs(1,n,inf);
return ret;
}
int main()
{
int t;
cin>>t;
int flag=1;
while(t--)
{
cin>>n>>m;
init();
for(int i=0;i>u>>v>>w;
add_edge(u,v,w);
}
cout<<"Case "< 优化:
/*
HDU3549
*/
#include
#include
#include
#include
#include
using namespace std;
const int MAXN = 10000 + 5;
const int MAXM = 100000 + 5;
const int INF = 1e9;
int n,m;
int s,t;//源点 汇点
int maxflow;//答案
struct Edge {
int next;
int to,flow;
} l[MAXM << 1];
int head[MAXN],cnt = 1;
int deep[MAXN],cur[MAXN];//deep记录bfs分层图每个点到源点的距离
queue q;
inline void add(int x,int y,int z) {
cnt++;
l[cnt].next = head[x];
l[cnt].to = y;
l[cnt].flow = z;
head[x] = cnt;
return;
}
int min(int x,int y) {
return x < y ? x : y;
}
int dfs(int now,int t,int lim) {//分别是当前点,汇点,当前边上最小的流量
if(!lim || now == t) return lim;//终止条件
// cout<<"DEBUG: DFS HAS BEEN RUN!"< INF && l[i].flow) {//有流量就增广
//deep我赋的初值是0x7f7f7f7f 大于 INF = 1e9)
deep[l[i].to] = deep[tmp] + 1;
q.push(l[i].to);
}
}
}
if(deep[t] < INF) return true;
else return false;
}
void dinic(int s,int t) {
while(bfs(s,t)) {
maxflow += dfs(s,t,INF);
// cout<<"DEBUG: BFS HAS BEEN RUN!"<>t;
while(t--)
{
init();
cin>>n>>m;//点数边数
int x,y,z;
for(int i = 1; i <= m; i++) {
scanf("%d%d%d",&x,&y,&z);
add(x,y,z);
add(y,x,0);
}
// cout<<"DEBUG: ADD FININSHED!"< 话说这到底优化了什么呢,我看到一篇博客说的很好哈:
每次增广一条路后可以看做“榨干”了这条路,既然榨干了就没有再增广的可能了。但如果每次都扫描这些“枯萎的”边是很浪费时间的。那我们就记录一下“榨取”到那条边了,然后下一次直接从这条边开始增广,就可以节省大量的时间。这就是 当前弧优化 。
在DFS中用cur[x]表示当前应该从x的编号为cur[x]的边开始访问,也就是说从0到cur[x]-1的这些边都不用再访问了,相当于删掉了(上面说的榨干),达到了满流。DFS(x,a)表示当前在x节点,有流量a,到终点t的最大流。当前弧优化在DFS里的关键点在if(a==0) break;也就是说对于结点x,如果x连接的前面一些弧已经能把a这么多的流量都送到终点,就不需要再去访问后面的一些弧了,当前未满的弧和后面未访问的弧等到下次再访问结点x的时候再去增广。
以上就是计算最大流的一些简单算法,再回到最开始的那个问题,怎么求最大匹配?
最大匹配:
匈牙利算法和em算法也是处理最大匹配的一个好算法,非常好用,但是呢,网络流更全面,除了最大匹配,还可以用在其他许许多多方面,比较万能吧!下面就最大流来求最大匹配:
超级原点与超级汇点:
想想就知道哈,二分图就是两个集合之间有联系,然而,就知道,他们有无数个源点与无数个汇点,所以呢,就要把它变换成只有一个源点与一个汇点的网络,这就需要超级原点与超级汇点!之后呢,就把每条边的流量改成1就迎刃而解了。
求最大匹配步骤:
(1)增加一个源点s和一个汇点t;
(2)从s向集合X的每一个顶点引一条有向边,从集合Y的每一个顶点向t引一条有向边;
(3)将原图的每条边改为从集合X向集合Y的有向边;
(4)置每条边的容量为1;
代码以后附上吧。。。
MCMF(最小费用最大流):
顾名思义,就是求最大流花费的最小费用,对于费用(就是最短路啊)可以用SPFA来解(不能用dij,因为反向边是负值),所以,就是在以上求最大流的基础上加上SPFA及妥妥的!
代码:
#include
#include
#include
#include
using namespace std;
const int maxn=100010;
bool vis[maxn];
int n,m,s,t,x,y,z,f,dis[maxn],pre[maxn],last[maxn],flow[maxn],maxflow,mincost;
struct Edge{
int to,next,flow,dis;
}edge[maxn];
int head[maxn],num_edge;
queue q;
void add_edge(int from,int to,int flow,int dis)
{
edge[++num_edge].next=head[from];
edge[num_edge].to=to;
edge[num_edge].flow=flow;
edge[num_edge].dis=dis;
head[from]=num_edge;
}
bool spfa(int s,int t)
{
memset(dis,0x7f,sizeof(dis));
memset(flow,0x7f,sizeof(flow));
memset(vis,0,sizeof(vis));
q.push(s); vis[s]=1; dis[s]=0; pre[t]=-1;
while (!q.empty())
{
int now=q.front();
q.pop();
vis[now]=0;
for (int i=head[now]; i!=-1; i=edge[i].next)
{
if (edge[i].flow>0 && dis[edge[i].to]>dis[now]+edge[i].dis)
{
dis[edge[i].to]=dis[now]+edge[i].dis;
pre[edge[i].to]=now;
last[edge[i].to]=i;
flow[edge[i].to]=min(flow[now],edge[i].flow);
if (!vis[edge[i].to])
{
vis[edge[i].to]=1;
q.push(edge[i].to);
}
}
}
}
return pre[t]!=-1;
}
void MCMF()
{
while (spfa(s,t))
{
int now=t;
maxflow+=flow[t];
mincost+=flow[t]*dis[t];
while (now!=s)
{
edge[last[now]].flow-=flow[t];
edge[last[now]^1].flow+=flow[t];
now=pre[now];
}
}
}
int main()
{
memset(head,-1,sizeof(head)); num_edge=-1;
scanf("%d%d%d%d",&n,&m,&s,&t);
for (int i=1; i<=m; i++)
{
scanf("%d%d%d%d",&x,&y,&z,&f);
add_edge(x,y,z,f); add_edge(y,x,0,-f);
}
MCMF();
printf("%d %d",maxflow,mincost);
return 0;
}
上下限有待更新。。。