题目部分
题目描述
给出N个圆,保证任意两个圆都相离,然后给出两个点(x1,y1)、(x2,y2),保证均不在某个圆上,要从点(x1,y1)到(x2,y2)画条曲线,问这条曲线最少穿过多少次圆的边界?
输入输出格式
输入格式:
第一行为一个整数N,表示圆的个数;
第二行是N个整数,表示N个圆的X坐标;
第三行是N个整数,表示N个圆的Y坐标;
第四行是N个整数,表示N个圆的半径R;
第五行是四个整数x1,y1,x2,y2.
【数据规模】
1≤N≤50,坐标范围[-1000,1000],每个圆的半径1<=R<=1000。
保证没有两个圆有公共点,起点和终点不会落到某个圆的边界上。
输出格式:
仅一个整数,表示最少要穿过多少次圆的边界。
输入输出样例
输入样例#1:
7
1 -3 2 5 -4 12 12
1 -1 2 5 5 1 1
8 1 2 1 1 1 2
-5 1 12 1输出样例#1:
3分析
所以,这题真的是。。。太厉害了
分析No.1(Wrong)
一开始以为只有四种情况:如图
1
2
3
4
所以
所以,只有三种答案:0,1,2
然而我发现:
对了:就是,有3?!!!!
mmpmmpmmpmmp
既然这样,我就生气了,所以
分析No.2
画图
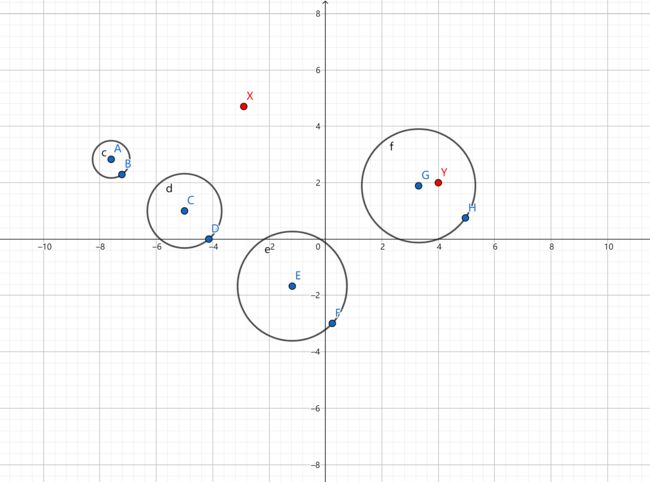
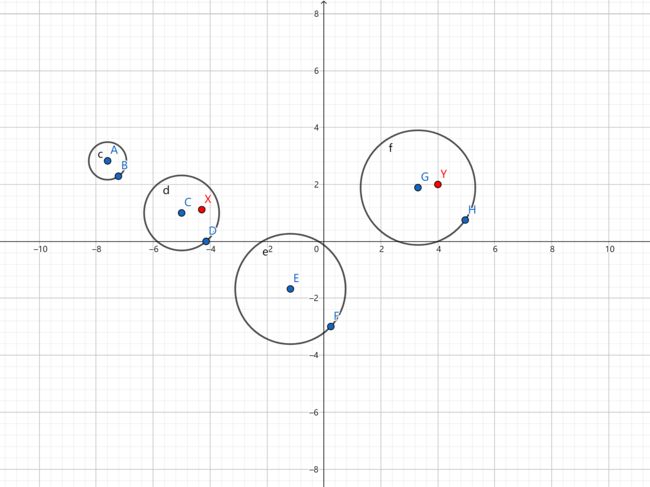
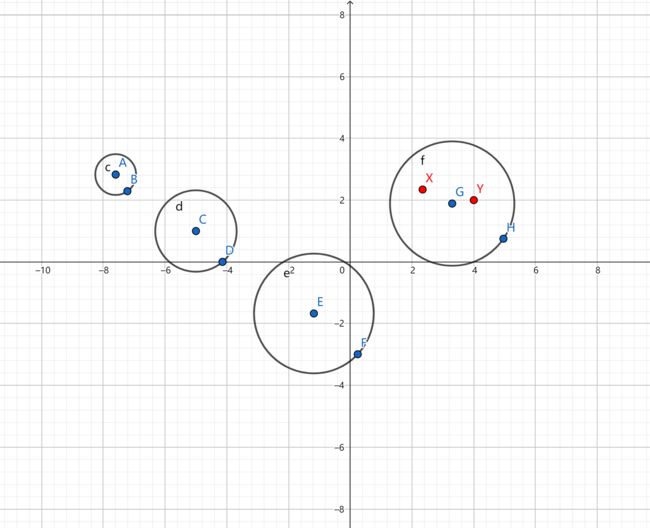
我把样例画了一下,然后发现。。。
发现
他所谓的相离, 包含内含!!!!
那就明了了,我说怎么会有3。。。
代码
#include
#include
#include
using namespace std;
int x[60],y[60];
double r[60];
int x1,yy,x2,y2;//这里不知道为什么用有y1会报错。。。可能是我没学到那种东西。。。
bool f1,f2;
int ans;
int main()
{
int n;
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&x[i]);
for(int i=1;i<=n;i++) scanf("%d",&y[i]);
for(int i=1;i<=n;i++) scanf("%lf",&r[i]);
scanf("%d%d%d%d",&x1,&yy,&x2,&y2);
for(int i=1;i<=n;i++)
{
double tmp1=sqrt(((x1-x[i])*(x1-x[i]))+((yy-y[i])*(yy-y[i])));
double tmp2=sqrt(((x2-x[i])*(x2-x[i]))+((y2-y[i])*(y2-y[i])));
if(tmp1 好了我记住了,分析样例,分析样例,分析样例!!!!!