\(\\\)
定义
介绍一些写法和数组的含义,首先要知道 字典序 。
- \(len\):字符串长度
\(s\):字符串数组,我们的字符串存储在 \(s[0]...s[len-1]\) 中。
\(suffix(i) ,i\in[0,len-1]\): 表示子串 \(s[i]...s[len-1]\),即从 \(i\) 开始的后缀 。
加入我们提取出了 \(suffix(1)...suffix(len-1)\) ,将他们按照字典序从小到达排序。
- \(sa[i]\) :排名为 \(i\) 的后缀的第一个字符在原串里的位置 。
- \(rank[i]\) :\(suffix(i)\) 的排名。
显然这两个数组可以在 \(O(N)\) 的时间内互相推出。
\(\\\)
Doubling Algorithm
由于博主太蒟并不会DC3,想看DC3的同志们可以溜了
\(\\\)
倍增构造法。
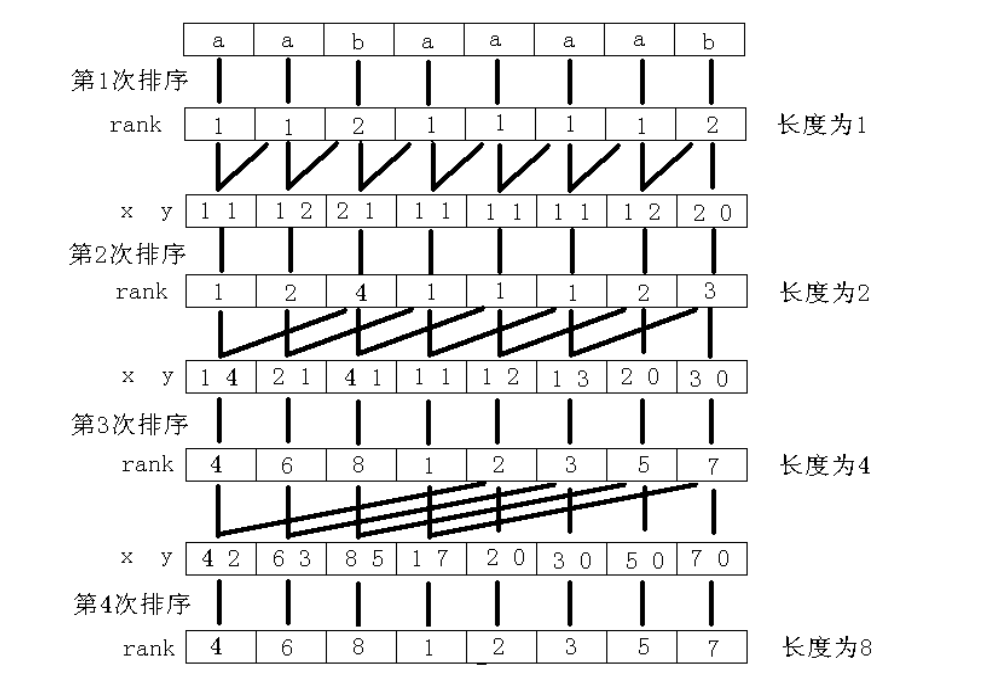
从小到大枚举 \(k\) ,每次按照字典序排序,每一个后缀的长度为 \(2^k\) 的前缀,直到没有相同排名的为止。
若有的后缀不够长就在后面补上:比当前串全字符集最小字符还要小的字符,结果显然符合字典序的定义。
\(\\\)
如何确定长度为 \(2^k\) 的每一个后缀对应前缀的排名?
倍增。有点像数学归纳法的感觉。
首先我们显然可以直接求出来 \(k=0\) 的答案。
然后对于一个 \(k\) ,我们显然已经完成了 \(k-1\) 部分的工作。
所以对于一个长度为 \(2^k\) 的前缀,它显然可以由两个长度为 \(2^{k-1}\) 的前缀拼成。
也就是说,我们可以把长度为 \(2^k\) 的前缀,写成两个长度为 \(2^{k-1}\) 的前缀的有序二元组。
有一个显然的结论,因为长度 \(2^{k-1}\) 的所有前缀有序,所以我们对这些二元组排序法则可以写成:
以前一个长度为 \(2^{k-1}\) 的前缀的 \(rank\) 为第一关键字,以后一个长度为 \(2^{k-1}\) 的前缀的 \(rank\) 为第二关键字排序。
对于此方法得到的顺序,与将整个长度为 \(2^k\) 的前缀字典序排序得到的顺序,想一想发现是相同的,因为它符合字典序定义。
\(\\\)
比较到什么时候为止?显然是求到一个 \(k\),使得每一个后缀 \(rank\) 不同时。
\(\\\)
附上 \(2009\) 年国家集训队论文中的排序图片,可以加深体会一下整个排序的思想。
\(\\\)
代码实现
下面重点说一下代码实现,算法的精华也就体现在这里。附上一个写的不错的博客 。
\(\\\)
再次声明一些数组的定义:
\(sa[i]\) :排名为 \(i\) 的后缀第一个字符在字符串内的位置,注意字符串数组是从 \(0\) 开始存储的。
需要注意的是,在倍增过程中 \(sa[i]\) 只表示对每一个后缀的长度为 \(2^k\) 的前缀排序的结果。
同时需要注意的是,在 \(rank\) 相同时我们按照第一个字符在字符串出现的位置从小到大排序。
\(x[i]\) :上面的 \(rank[i]\) 我们在这里写作 \(x[i]\) ,含义还是 \(suffix(i)\) 的排名。
同理,在倍增过程中,\(x[i]\) 只表示每一个后缀的长度为 \(2^k\) 的前缀的排名,两个位置的 \(x\) 可以相同。
\(y[i]\) :排序时的辅助数组,代表二元组的第二个元素排序的结果。
其中 \(y[i]\) 表示 排名为 \(i\) 的第二个长度为 \(2^{k-1}\) 的前缀,对应整个前缀的开头位置 。
注意,此时下标表示名次,值代表第二关键字的首字符位置,与 \(x\) 数组的定义为逆运算。
\(cnt[i]\) :计数器数组,用于基数排序。
\(\\\)
第一步,将长度为 \(1\) 的每一个字符排序。
这个过程就是基数排序。过程中的 \(n\) 表示数组长度,\(m\) 表示原串字符集范围为 \([1,m-1]\) 。
注意体会最后一行的倒序循环,此时体现了 \(rank\) 相同时按照第一个字符在字符串出现的位置排序的原则。
for(R int i=0;i\(\\\)
然后我们就要开始倍增构造,设 \(k\) 直接表示当前考虑的前缀长度。
for(R int k=1,p=0;k<=n;k<<=1)\(\\\)
首先看本次排序构造的 \(y[i]\) 。
由于 \(sa\) 数组是有序的,所以我们没必要对 \(y[i]\) 数组进行一次基数排序。
p=0;
for(R int i=n-k;i=k) y[p++]=sa[i]-k; 第二行的含义是,因为字符串的后 \(k\) 个后缀一定不能再找到长度为 \(k\) 的后缀继续拼接了。
根据字典序的定义,空串字典序优于任何一个字符串,所以他们的 \(y\) 应该最靠前。
同时因为 \(rank\) 相同时按照第一个字符在字符串出现的位置排序的原则,循环是正序。
第三行的含义是,如果一个长度为 \(k\) 的前缀起始位置 \(\le k\) ,那它必然作为一个后一段接在前面的某一个位置上。
可以注意到的是, \(sa\) 数组和 \(y\) 数组的定义形式是一致的,也就是说, 我们按照 \(sa\) 的顺序构造 \(y\) 没有问题。
\(\\\)
然后就要构造 \(sa[i]\) 。这也是构造过程中最精华的一部分。
for(R int i=0;i这其实是一个双关键字基数排序的过程。
双关键字基数排序时,我们需要先将第二关键字直接排序,然后再使用上面的代码。
现在 \(y[i]\) 显然已经是有序的了。
这个过程的理解可以参考最开始的单关键字基数排序。
为什么那时我们做到了在 \(rank\) 相同时我们按照第一个字符在字符串出现的位置从小到大排序的要求?
因为我们是倒着扫描的。
同理,为了让 \(x\) 相同的 \(y\) 越劣的越靠后,我们直接倒着扫描 \(y\) 不就可以了吗!
此时我们成功在 \(sa\) 数组内完成了第一第二关键字合并后的排序。
\(\\\)
然后要做的就是还原 \(rank\) 数组了。
注意 \(rank\) 数组的定义中可以有相同的排名,所以第一第二关键字 \(rank\) 相同的注意要特殊对待。
inline bool cmp(int *a,int x,int y,int k){return a[x]==a[y]&&a[x+k]==a[y+k];}
swap(x,y); p=1; x[sa[0]]=0;
for(R int i=1;i注意这个指针交换的过程,它优化掉了 \(swap\) 两个数组的复杂度。
因为 \(x\) 数组是上一个 \(k\) 的 \(rank\) 结果,所以可以直接比对新的即将拼合的两段是否相同。
\(\\\)
最后还有一个小优化。
if(p>=n) break;
m=p;就是 \(p=n\) 时,可以发现当前长度的前缀已经具有了区分每一个后缀的作用,所以我们没必要继续比下去了。
同时,上一次不同 \(rank\) 的个数显然是下一次基数排序的字符集大小。
\(\\\)
最后再多说一句,值得注意的是,不管是哪种实现方式,除了空字符外 \(rank\) 必须从 1 开始,否则会造成最小字符与空字符运行时混淆。
\(\\\)
一道例题
给出一个字符串,写出其所有循环同构串,将其按字典序从小大排序,输出排序后每一个串的尾字符。
\(\\\)
环的问题一般可以破环成链去搞。
拆开之后复制一倍接在后面,直接跑后缀数组,按 \(sa\) 顺序输出所有长度大于 \(len\) 的后缀对应答案。
\(\\\)
#include
#include
#include
#include
#include
#include
#include
#define N 200005
#define R register
using namespace std;
char ss[N];
int s[N],sa[N],cnt[N],t1[N],t2[N];
void da(int n,int m){
int *x=t1,*y=t2;
s[n++]=0;
for(R int i=0;i=k) y[p++]=sa[i]-k;
for(R int i=0;i