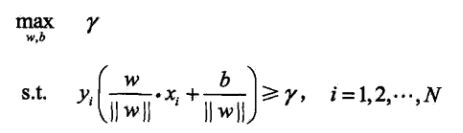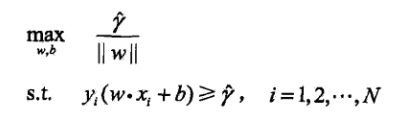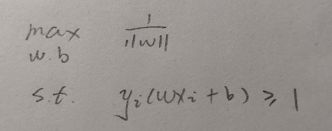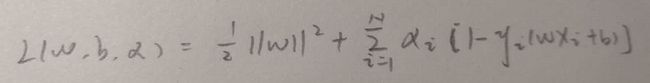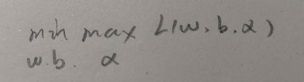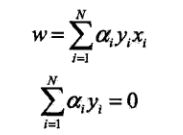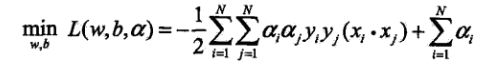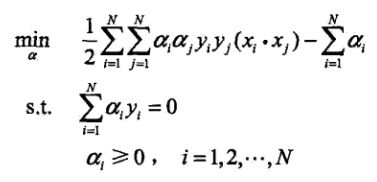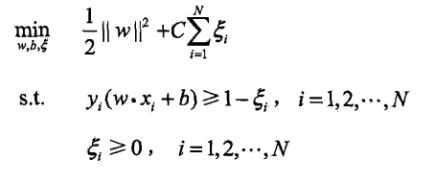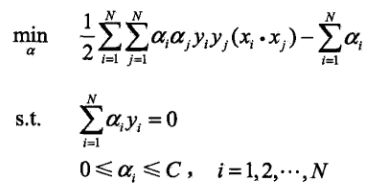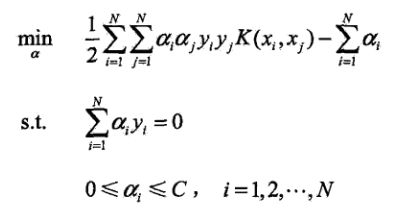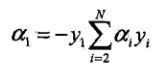统计学习方法|支持向量机(SVM)原理剖析及实现

欢迎直接到我的博客查看最近文章：www.pkudodo.com。更新会比较快，评论回复我也能比较快看见，排版也会更好一点。

原始blog链接： http://www.pkudodo.com/2018/12/16/1-8/

 

前言

《统计学习方法》一书在前几天正式看完，由于这本书在一定程度上对于初学者是有一些难度的，趁着热乎劲把自己走过的弯路都写出来，后人也能走得更顺畅一点。

以下是我的github地址，其中有《统计学习方法》书中所有涉及到的算法的实现，也是在写博客的同时编写的。在编写宗旨上是希望所有人看完书以后，按照程序的思路再配合书中的公式，能知道怎么讲所学的都应用上。（有点自恋地讲）程序中的注释可能比大部分的博客内容都多。希望大家能够多多捧场，如果可以的话，为我的github打颗星，也能让更多的人看到。

github：

GitHub|手写实现李航《统计学习方法》书中全部算法

相关博文：

1. 统计学习方法|感知机原理剖析及实现
2. 统计学习方法|K近邻原理剖析及实现
3. 统计学习方法|朴素贝叶斯原理剖析及实现
4. 统计学习方法|决策树原理剖析及实现
5. 统计学习方法|逻辑斯蒂原理剖析及实现
6. 统计学习方法|最大熵原理剖析及实现
7. 统计学习方法|支持向量机(SVM)原理剖析及实现

 

 

正文

SVM的直观理解

在刚踏入机器学习世界时，经常会听到周围讨论SVM的声音，很多时候一讨论SVM，周围的人好像就会开始瞪大了眼睛看你，仿佛在说这你都能懂？当然了，这件事情也许是个个例，但确实在初学的我身边发生过几回。有趣的是，当大家都学会了SVM以后，反而讨论的人少了。

当我真正感觉到学会了SVM以后，我突然发现其实SVM也就那样。如果你再仔细回想一下，学习机器学习前是不是感觉人工智能好高大上，现在几个模型走下来，心里也就没有多大的波澜起伏了。

有感而发说起这些，想让读者在阅读前先知道，SVM不是什么很难的算法。当你跟着本文走完以后，可能会感叹一下前人的智慧，但绝不会仍然觉得这是一个很难的模型。

好了，我们正式开始。

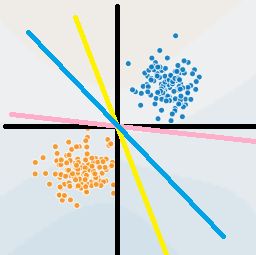
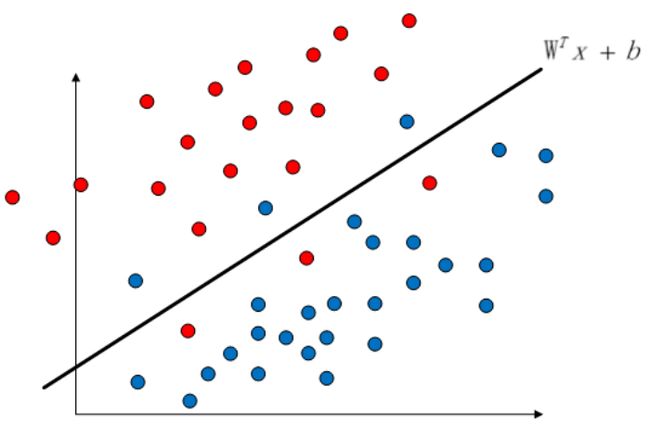
机器学习算法中可以说预测一个样本所属的类是一件很重要的事情。我们在过去的几个模型中通常做法是给定训练集，划分超平面，预测样本所在类。那我们不得不重新拿出感知机中给出的这张图：

感知机和逻辑斯蒂都是属于划分一个超平面来对点进行划分的模型，就像图中蓝点和黄点中间的几条线一样。在当时我们也分析过，从图上直观来看，我们认为似乎蓝色的超平面更好一点，但实际上感知机和逻辑斯蒂回归都没有找到一个最佳的超平面，那么有没有一个办法去找到最好的这个蓝色的超平面呢？也就是说：

有没有一种算法能够找到最优划分超平面？

SVM可以，但在介绍SVM前，我们首先需要讨论一个问题：我们试图找到最优的超平面，但我们还没有给出过定义什么样的超平面是最优的。我们给出下面这张图：

图中有红蓝两类，分别标记为圆圈和方框。图中存在A、B、C三个超平面，很明显我们感觉A是三个超平面中最优的（实际上SVM找到的仍然不是一个最优的超平面，但一定在最优附近，本文的最优是相对于感知机、逻辑斯蒂等算法而言。望读者了解其中的细节），为什么最优？因为它与两个类的距离都足够大。那定义上的距离该怎么描述？

我们看上面这张图，也许可以给出这样一个定义：两个类中距离超平面最近的那个点的距离要足够大。比如说超平面C，距离1和6就太近了，B距离4和5太近了。怎么算太近？我们看A，最近的可能是4、5、1、2，很明显它们的距离都比B、C的大，所以A是最优的。

SVM就是基于这样一个理论，它试图去找到一个超平面，这个超平面可以使得与它最近的样本点的距离必须大于其他所有超平面划分时与最近的样本点的距离。在SVM当中这叫间隔最大化。

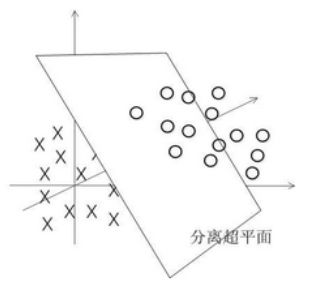
此外SVM还解决了一个问题，就是我们之前划分样本时解决背景是在可以用一个超平面划分的情况下。比如说在之前的例子中两类点是可以很明显分开的，那如果是下面这张图呢？

可能用一个线性的超平面就不太够了。所以我们的超平面是上图中的一个圆圈？这好像不太对劲。但是我们都知道样本中的每一个点都是真实的点，我们也许就在二维平面上表示是不太够的，也许我们在三维空间中将样本一个个地描述出来是下面这样的。

那在三维中我们依然可以用一个超平面去表示。读者可能要问：

你怎么就能确信在三维中一定是上面这张图？如果他们依然是像第一张图一样一类点在中间，另一类点像个篮球皮一样把它包住呢？

我当时也有这个疑惑，事实上我们可以想象一个情景：我们假想有一根棍子，但是它是垂直地对着你的眼睛的，只能看到棍子的一端，就好像有人拿着棍子指着你一样，你只能看到棍子的那个横截面。如果这是根透明的棍子，在棍子上分布着两个点，但是你从横截面看过去，只有一个点。这是一维的情况。

如果升到二维呢？就是对面拿着棍子那个人，把棍子横着给你看，整条根子就像线一样，那你就能很清楚地看到两个点。那有没有一维线性不可分，二维仍然线性不可分的情况呢？有。我们假想棍子里有10个点，5个红点5个黑点，但他们是交错排布的，在棍子中（红，黑，红，黑......红，黑）这样的顺序，我们仍然不能用一把刀把它们一切为二进行划分。

所以我们可以提升到三维，这时候棍子真的成了棍子，它有体积，它很长，同时是个圆柱体。如果把棍子竖直地放在地上然后仔细观察内部的10个点，也许我们会发现红点全在向南面，黑点全在向北面，这是我们可以拿把砍刀把棍子一劈为二，就能划分开来了。

那如果三维中仍然不线性可分呢？就好像上面的例子一样，红点在棍子内部正中间，黑点像个篮球皮一样把它包起来。这是完全可能存在的，所以我们需要到四维的情况下再去判断。

这就好像一场博弈，我们每失败一次，就升维一次，直到某一维N时两类点出现了一个失误，他们线性可分了。

这就是SVM解决线性不可分的过程，但它并不是逐渐升维的，而是直接上升到无穷维。

为什么是无穷维？

我们去找具体是第几维这种过程太复杂了，事实上我们的维度只需要大于等于N维就可以了，所以考虑到所有的应用场景、不同问题下的样本特征，我们直接上升到无穷维使得其必定可以线性可分。

为什么样本随着维度的升高一定是线性可分的？有没有存在无穷维也不可分的情况呢？

没有，样本之间只要存在差异，也就是说只要不是相同的样本点，一定能在某种程度上对其进行区分。就好像上面棍子的例子一样，我们无法划分，只是维度太低观察到的信息不够。随着维度的上升，我们的信息量越来越充足，只要是有差异的样本并且找到其差异，一定能够使用该差异来划分的。

为什么大于N维也可以？会不会存在大于N维的某一维又突然线性不可分了呢？

不会，就像上一个问题一样，当你在某一维突然获取到了能够划分样本的足够多的信息后，随着维度的上升，我们得到的信息量只会越来越多，而第N维的信息量就足够我们划分了，更多的信息量并不会出现问题中的这种情况。

 

写到这里，除了直观认知以外，我希望能用数学角度来阐述一下上面的问题。当然了，并不涉及公式，也许称为数学的直观角度更合理一点。

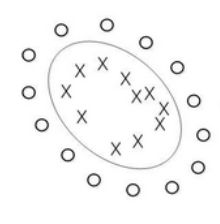
在讨论这种有趣的现象时，我希望能够将讨论限制在二维内，这样更直观，所以在二维中的划分超平面wx+b也许可以写成ax+b。我们无数次见过并且用过ax+b这个式子，那么下面这张图中的圆圈我们怎么表示呢？

为了方便讨论，我们假设上面的圆圈是个正儿八经地圆（虽然是个椭圆），圆心是坐标原点，直径为1,。那么它的公式是：x²+y²=1。

事实上我们不得不承认，如果划分超平面的公式是x²+y²=1，我们也能完美地划分这两类点不是吗？但是你发现一个有趣的事情没有，x的幂是平方了，也可以说，它升维了。

如果按照我们上面例子说的，在三维中x点在内部，O点像篮球皮一样包起来了呢？回忆一下x³+y³+z³=1。

变成三次方了，再次升维。

但是SVM实际上最后产出的超平面仍然是wx+b的形式，x仍然是1次方，问题在于我们上面的讨论是将超平面变形，但在SVM中，我们是将坐标轴变形，举个例子就像x轴上的每个数x转换成2x，那轴还是轴，但坐标轴中的图形在x轴方向上被压缩到了原来的1/2，坐标轴内的图形也就跟着变形了。

所以数学上来讲，SVM中升维的过程本质上是变换坐标轴，就好像捏橡皮泥一样不停地变换内部的图形，而升的维度越高，变形也就能越复杂。到最后也就越能直接线性可分。

 

总结一下，SVM通过上面的思路主要解决了两类问题：

1.寻找到最优的超平面

2.能够划分非线性可分的样本

 

SVM的数学角度（配合《统计学习方法》食用更佳）

在引出数学公式前，我们回忆一下上文中SVM寻找最优超平面的过程，其中涉及到了距离的计算。但凡涉及到距离，我们不得不谈一下几何间隔和函数间隔的差别。在感知机一节中我们已经提到过相关概念，但考虑到部分读者可能对其还不是很了解，因此简单做个介绍，如果阅读完还是感觉有些不太明白的，可以阅读感知器一节。

以划分超平面为原理支撑的模型通常会使用wx+b，用wx+b=0表示超平面。当要预测一个样本x1时，我们将其代入wx1+b通过结果的正负来判断是在超平面的左侧还是右侧。若结果为wx1+b=h，将h取绝对值后也就是该样本点与超平面之间的距离大小。

例如SVM我们虽然还不太清楚内部原理，但涉及到将超平面与样本点之间的间距最大化，我们假设间距为h，那么h=wx1+b，等同于在运算过程中一定会涉及将wx1+b最大化。同时我们一定要记住wx+b=0这个式子，w和h也就是说要遵循wx+b=0这个约束。如果此时我让w和b同时增大为2w和2b呢？2wx+b=0仍然满足超平面的需要，但此时对于要预测的样本x1来说，2wx1+2b=2h，距离增大为原先的二倍了。这也就意味着，我不需要去找什么最优的划分超平面，我只要不停地等比例增大w和b就可以了。在寻找最优超平面的过程中，这是绝对不允许的。这里的距离，被称为函数间隔。

那什么是几何间隔？我们知道w是超平面的单位法向量，所以会将wx+b=0转换成w/||w|| * x + b/||w||。简单来说，w就好像现实世界的单位——米一样，我如果将其变为2倍，比如说有个大高个原先身高1.8米，那现在可能量完身高发现是3.6米了——函数间距增大了，与此同时单位米从原先的1米变为2米，也就是说我们原先长度为1米的东西变成了2米，这时候将我们的长度重新除以这个2米，又变回了1.8m。这就是几何间距，可以认为是物理意义上现实的距离，并不会因为参照物单位的增大缩小而发生变化。因为大高个自始至终都是1.8米。

显然，在进行距离最大化的过程中，我们需要使用几何间隔。

间隔最大化

我们需要找到一个超平面，该超平面使得其最近的点的距离始终大于其他超平面与最近点的距离。我们可以找到它的一个对偶的说法：

我们要找到一个超平面，它与样本点中最近的样本点的距离是所有超平面中最远。

一个最近一个最远，有点绕嘴，换句话说，就是再也找不到另一个超平面，能够和样本点隔开这么远的距离了。我们假设这个距离是γ，所有有了下面的式子：

γ是所有样本与超平面之间的距离，就是所有的样本的距离都要大于这个γ，于此同时我们要最大化γ。需要注意的是，SVM遵循了感知机和逻辑斯蒂的一贯做法，反正例分别为+1和-1，当在超平面左边时，距离为负，反之为正。所以在第2行的约束中求得几何间隔后要乘以yi，保证结果一定为正。

为了写得更简单一点，我们通常会写成下面这样，实际上两个式子是相同的。（γ上面带帽表示该γ是函数间隔，做除法以后就变回几何间隔了）

要主要到γ帽是函数间隔，我们如果增大和缩小w，实际上是可以改变γ帽的值得，但与此同时除以了||w||，在求解的过程中没有影响。所以为了简化运算，我们可以假设w和b等比例缩放成γ帽为1的一个值，就变成了下式：

如果将第一行中的w移到分子上去，max同时变成min，继而变成下式：

可能有读者发现约束条件中书上用的是大于等于，我用的是小于等于，实际上小于等于才是符合正常写法的。

此外要注意的是w的平方和前面的1/2只是为了后续的运算方便。实际上在最小化过程中，1/2和平方并没有影响。（读者可以发现该式求导以后很干净，主要是为了这一方便）

所以我们只需要找到满足上式约束，同时||w||最小的w即可，通过w继而求得最优的b。（关于超平面的存在性和唯一性书中证明看似复杂其实原理很朴素，本文不再阐述。）

有了约束以后，一切看起来就又和以前一样了，拉格朗日乘子法干起来。

进而求

有些人会有疑惑，这是啥？

我们先不看外面的min，内部对α求max，也就是说此时求L的最大值，但只有α是参数，w和b是常数。

我们回忆一下以前我们写出拉格朗日乘子法时，是对其求导然后得0，现在只不过把求的是极大值还是极小值写出来而已，并没有什么差别。

那为什么是max而不是min呢？都是极值呀

我们需要仔细观察一下，如果我们最后求得的参数是符合约束的，那么1-yi(wxi+b)也就必定小于等于0，而α依据拉格朗日乘子法的规则是一定要大于0的，也就是说L最后的结果一定会小于1/2*||w||，它只有最大值没有最小值，所以这里用的是max。

于此同时我们不要忘记了最后要求的是1/2*||w||的最小值，所以再将w和b作为参数，求得最小值。所以也就是求极小极大值。

但为了计算上的方便，我们通常会转换成极大极小值，也就是：

为什么这两个等价？

实际上对于任何函数而言，maxminf(x)<=minmaxf(x)，正是依据这一理论，我们需要求最小值，那我们通过转换求一个更小值，也一点问题都没有。

那什么时候等号成立呢？建议读者自行去详细查阅一下。其实从很不严谨地角度来说，如果约束的那个小于等于变成小于号，等号就成立。

既然对偶形式的式子也有了，那就先求minL吧，对w求偏导令为0：

得到了两个结果，将其代入L原式中，得到下式：

代入到外面的max中，取个负号变成求min：

到这里可以暂停一个段落休息会了，我们已经得到了要求的最小值，同时需要满足约束。此时w可以表示为：

此外根据KKT互补条件可得：

关于KKT条件本文不打算过多展开，不了解的可以查阅相关资料，这部分资料网上比较容易找到。

那么我们这里要分析一件事情，w最后依赖于上式等号后面的求和项，w是不可能等于0的（书中有证明，较为简单），那么最后产生的w如果要有意义，α >= 0中必然会存在某些α是大于0的（如果等于0的话，那一项就是0了），于此同时注意上式KKT中的出来的条件，当α不等于0是，后面括号内的一定是0。这代表了该样本点x与超平面的间隔是1。对1眼熟吗？我们在最前面时提到了令γ帽=1，这表示了它就是离超平面最近的那个点。也被称为支持向量。

所以最后发现了一个很有意思的现象，算到最后对w的计算有意义的竟然只有那些离超平面距离为1的样本点，也就是支持向量，其他的样本多几个少几个对w一点意义都没有，因为在求和式中都是0了。

这也是为什么SVM速度比较慢的原因，它要去遍历样本来找到最近的这些点，然后再去计算得到w。

我们现在已经知道该怎么去找这个最优的超平面了，但还有一片乌云盘旋在我们脑袋上空：

如果样本有噪音呢？比如说下面的图：

按照之前的算法，这个超平面就没法计算出来了，因为我们不可能找到一条这样的直线去满足我们之前的约束。所以引入了一个新的概念——软间隔

我们都知道原式yi(wx+b)>=1保证的是所有的样本点与超平面的距离都大于1，那么现在引入一个松弛变量，比如说松弛变量四0.1，那么所有样本之间的距离只需要大于0.9即可了，如果噪音仍然不能被包含进去，那就再增大一点松弛变量。就像它的名字一样，将距离的要求进行放宽，以此满足噪音的情况。

于此同时我们的约束也要修改：

在min式子中加入了松弛变量的求和，称为惩罚项。就像名字说的一样，我们不能一味地去放宽限制以此来满足噪音的存在，如果放宽的太多了，min式子就会相应的变大，也就不再是求最小问题了，这时候需要惩罚。C是调和系数，如果C很小，那么松弛变量就能相应地设置得大一点，因为乘上C之后再总式子中体现地就很小了。C决定了我们想让这个SVM有多软还是多硬。

关于软间隔我不打算做一些展开，因为书中内容还是比较简单的，总体来说引入了松弛变量和C之后，最大的变化是根据KKT条件得到0<=αi<=C，之后所有发生的变化都是围绕着α的范围改变而展开的。最后得到：

之后我们要做的就是求得满足条件地所有αi的值，然后再以此求得

 

核函数

我们现在已经知道求得满足约束并找到最优解的α即可，之后通过w的计算公式根据α求得，而w知道后将w带入wx+b=0也可知道b。目前来看我们掌握的信息已经足够支撑我们找到一个最优超平面了。实际上后续的核函数已经SMO都是在进行一个优化的过程，知道它们最终只是为优化做服务以后，学起来似乎也没有那么难的。事实上，目前你已经掌握了SMV不是吗？只不过这样子直接寻找最优解，比别人慢了很多很多而已。

要引出核函数，我们重新看下面这张图：

我们看min后面这个式子，其中α和y都是标量，直接计算就可以，唯一让人难受的是xi与xj的点积，它是向量之间的点积，同时前面有求和项，也就是说在计算过程中是需要计算任意两个向量之间的点积的。这里就引申出一个问题，例如在Mnist数据集中，训练集有6万个样本，也就是6万个向量，现在计算机速度越来越快了，6万*6万个标量还行，算起来没多久，可是如果是向量呢？Mnist中每个向量由784维，也就是说单独的两个向量点积就需要784次运算，再加上6万个样本，其实速度是非常慢的。

关于核函数的有效性及相关证明书上有详细说明，把大段公式搬到文章里可能不是我想做的。所以这里我提一下核函数的核心概念，我相信在了解了核函数的运行机理后再去看证明过程会好很多。

我们先看一个式子，它就是核函数，核函数就是为了解决这个问题而提出的：

有两个高维向量分别是x和z，那么x与z的点积等于上面的K(x, z)。什么意思？

我们先将概念理一遍，由于公式的需要，我们目前需要计算向量x和z的点积（公式中是xi和xj），我们可以使用核函数将其映射到高维空间去（还记得SVM可以在高维空间中划分原先非线性的样本吗？），在高维空间中再运行但SVM，使得划分非线性样本成为可能。另一方面，点积的两个样本维度都很高，我们可以使用核函数方便地通过另一种方式去计算，结果是一样的，同样减少了复杂度，使得算法能够在有限的时间内计算完成。

那怎么使用呢？很简单，将上文中所有xi和xj的点积替换为K(x, z)即可。在SVM中我们通常使用的是高斯核：

也就是在计算x和z的点积时，只需要计算上面的式子就好了。

 

序列最小最优化算法

这是SVM的最后一个部分了，老实说每次写博客都写挺累的，昨天晚上十点写到1点将第一部分写完，刚才吃过午饭从核函数开始写，想把脑子里的东西拿出来让所有人都明白是一件不太容易的事。

我们将核函数代入后重新回顾这个式子：

其式子中α是一个仍然存在的未知数，但其他好像我们目前都是可以得到的。那我们怎么求解这个问题的最优解呢？有一个定理是这样的：如果一个问题是最优解，那么它一定满足KKT条件，如果不满足，一定不是最优解，这是充分必要条件。所以这里引发出了一个思考，如果我们找到了最优解，那α的取值一定是满足KKT条件地。所以我需要不断得去调整α的值，直到最后所有的α都满足KKT条件，这时候我一定得到了最优解。

那么该怎么调整呢？有个算法叫SMO。

它的核心是这样的：我们有N个α（有α1、α2、....αN），这么多参数，咱们没法一下子全部知道哪个α值是哪个啊。这样，我先把其他α都当成参数，先找α1，让α1满足KKT，但是咱们要想起来上图中的第一个约束，它是一个求和式子，和必须为0。里面的每一项是一个α，如果我们只将其中一个α作为优化变量，比如说α1，那么其实可以直接求得α1：

也就没有办法再优化了，解决的办法是同时优化两个α，我们下面都以α1和α2举例：

又因为在下图的求最优式子中只有α1和α2，所以可以进行改写，将作为常数的α去掉。

整理以后变成下式：

关于α1和α2的优化问题，我觉得手写过程可能会更容易理解一点：

 

 

在图中最后的线与曲线的交点就是最优的α2，得到α2以后α1也就有了。但必须要考虑一个问题，如果交点在0-C的范围外，也就是说如果α大于C，那必须将其限制到C，如果小于0，必须限制为0。

实际上这只是其中的一条曲线，根据y1和y2值的不同，可能存在以下两种情形：

我希望读者能自己推自己推以下在这两种情况下α不同的取值，这里直接给出结果：

好了，现在从里面拿出两个α，怎么优化已经知道了，那我们该怎么从那么多个α里面去拿出两个呢？所有α两两组合吗？那如果样本数目很大的话，也太慢了，如何挑选合适的两个α就是SMO的核心所在。

 

SMO变量的选择方法

第一个变量的选择

我们选择违反KKT条件最严重的点。我们都知道最终的目的就是让所有的α都符合KKT条件，那么在找第一个的时候，我们倾向于最不符合KKT条件的，这样子步子能迈得大一点，从KKT条件上来看，也就是：

可以通过量化违反的程度来判断哪个违反的最严重，每次遍历样本找到违反最严重的。但我在程序中并没有这么做，而是直接遍历，找到的第一个违反KKT的就作为第一个变量。怎么说呢，其实效果也还好，我没有测过找最严重的时间会多长。我这么做的理由主要是发现几乎所有α都违反，每次遍历找最违反感觉有点慢。可能是我理解还没到位吧，在程序中读者看到这一部分的时候，希望不要对此感到疑惑。

第二个变量的选择

第二个变量选择的宗旨就是在原先步子迈得比较大的情况下，再找一个步子迈得最大的α。它的量化方式是|E1-E2|，其中Ei的计算方式是：

在程序中我对于E做了一些小的修改，但选择原理其实是不变的。主要是SVM如果照着书上说的没有任何的优化方法，那实在是跑得太慢了。所以在第二个变量的选择中，我将范围做了一些限制，详细可以在我的注释中看到。

两个α都找到一个，进行优化，然后找下一对α，直到再也找不到不违反KKT的α了为止。α求得以后，w也就顺理成章能够得到了，之后再得到b，也没啥好说的，就不细说了。

 

以上就是SVM的全部理论了。

贴代码：（建议去本文最上方的github链接下载，有书中所有算法的实现以及详细注释）

#coding=utf-8
#Author:Dodo
#Date:2018-12-03
#Email:[email protected]
#Blog:www.pkudodo.com
'''
数据集：Mnist
训练集数量：60000(实际使用：1000)
测试集数量：10000（实际使用：100)
------------------------------
运行结果：
    正确率：99%
    运行时长：50s
'''

import time
import numpy as np
import math
import random

def loadData(fileName):
    '''
    加载文件
    :param fileName:要加载的文件路径
    :return: 数据集和标签集
    '''
    #存放数据及标记
    dataArr = []; labelArr = []
    #读取文件
    fr = open(fileName)
    #遍历文件中的每一行
    for line in fr.readlines():
        #获取当前行，并按“，”切割成字段放入列表中
        #strip：去掉每行字符串首尾指定的字符（默认空格或换行符）
        #split：按照指定的字符将字符串切割成每个字段，返回列表形式
        curLine = line.strip().split(',')
        #将每行中除标记外的数据放入数据集中（curLine[0]为标记信息）
        #在放入的同时将原先字符串形式的数据转换为0-1的浮点型
        dataArr.append([int(num) / 255 for num in curLine[1:]])
        #将标记信息放入标记集中
        #放入的同时将标记转换为整型
        #数字0标记为1  其余标记为-1
        if int(curLine[0]) == 0:
            labelArr.append(1)
        else:
            labelArr.append(-1)
    #返回数据集和标记
    return dataArr, labelArr

class SVM:
    '''
    SVM类
    '''
    def __init__(self, trainDataList, trainLabelList, sigma = 10, C = 200, toler = 0.001):
        '''
        SVM相关参数初始化
        :param trainDataList:训练数据集
        :param trainLabelList: 训练测试集
        :param sigma: 高斯核中分母的σ
        :param C:软间隔中的惩罚参数
        :param toler:松弛变量
        注：
        关于这些参数的初始值：参数的初始值大部分没有强要求，请参照书中给的参考，例如C是调和间隔与误分类点的系数，
            在选值时通过经验法依据结果来动态调整。（本程序中的初始值参考于《机器学习实战》中SVM章节，因为书中也
            使用了该数据集，只不过抽取了很少的数据测试。参数在一定程度上有参考性。）
            如果使用的是其他数据集且结果不太好，强烈建议重新通读所有参数所在的公式进行修改。例如在核函数中σ的值
            高度依赖样本特征值范围，特征值范围较大时若不相应增大σ会导致所有计算得到的核函数均为0
        '''
        self.trainDataMat = np.mat(trainDataList)       #训练数据集
        self.trainLabelMat = np.mat(trainLabelList).T   #训练标签集，为了方便后续运算提前做了转置，变为列向量

        self.m, self.n = np.shape(self.trainDataMat)    #m：训练集数量    n：样本特征数目
        self.sigma = sigma                              #高斯核分母中的σ
        self.C = C                                      #惩罚参数
        self.toler = toler                              #松弛变量

        self.k = self.calcKernel()                      #核函数（初始化时提前计算）
        self.b = 0                                      #SVM中的偏置b
        self.alpha = [0] * self.trainDataMat.shape[0]   # α 长度为训练集数目
        self.E = [0 * self.trainLabelMat[i, 0] for i in range(self.trainLabelMat.shape[0])]     #SMO运算过程中的Ei
        self.supportVecIndex = []


    def calcKernel(self):
        '''
        计算核函数
        使用的是高斯核 详见“7.3.3 常用核函数” 式7.90
        :return: 高斯核矩阵
        '''
        #初始化高斯核结果矩阵 大小 = 训练集长度m * 训练集长度m
        #k[i][j] = Xi * Xj
        k = [[0 for i in range(self.m)] for j in range(self.m)]

        #大循环遍历Xi，Xi为式7.90中的x
        for i in range(self.m):
            #每100个打印一次
            #不能每次都打印，会极大拖慢程序运行速度
            #因为print是比较慢的
            if i % 100 == 0:
                print('construct the kernel:', i, self.m)
            #得到式7.90中的X
            X = self.trainDataMat[i, :]
            #小循环遍历Xj，Xj为式7.90中的Z
            # 由于 Xi * Xj 等于 Xj * Xi，一次计算得到的结果可以
            # 同时放在k[i][j]和k[j][i]中，这样一个矩阵只需要计算一半即可
            #所以小循环直接从i开始
            for j in range(i, self.m):
                #获得Z
                Z = self.trainDataMat[j, :]
                #先计算||X - Z||^2
                result = (X - Z) * (X - Z).T
                #分子除以分母后去指数，得到的即为高斯核结果
                result = np.exp(-1 * result / (2 * self.sigma**2))
                #将Xi*Xj的结果存放入k[i][j]和k[j][i]中
                k[i][j] = result
                k[j][i] = result
        #返回高斯核矩阵
        return k

    def isSatisfyKKT(self, i):
        '''
        查看第i个α是否满足KKT条件
        :param i:α的下标
        :return:
            True：满足
            False：不满足
        '''
        gxi =self.calc_gxi(i)
        yi = self.trainLabelMat[i]

        #判断依据参照“7.4.2 变量的选择方法”中“1.第1个变量的选择”
        #式7.111到7.113
        #--------------------
        #依据7.111
        if (math.fabs(self.alpha[i]) < self.toler) and (yi * gxi >= 1):
            return True
        #依据7.113
        elif (math.fabs(self.alpha[i] - self.C) < self.toler) and (yi * gxi <= 1):
            return True
        #依据7.112
        elif (self.alpha[i] > -self.toler) and (self.alpha[i] < (self.C + self.toler)) \
                and (math.fabs(yi * gxi - 1) < self.toler):
            return True

        return False

    def calc_gxi(self, i):
        '''
        计算g(xi)
        依据“7.101 两个变量二次规划的求解方法”式7.104
        :param i:x的下标
        :return: g(xi)的值
        '''
        #初始化g(xi)
        gxi = 0
        #因为g(xi)是一个求和式+b的形式，普通做法应该是直接求出求和式中的每一项再相加即可
        #但是读者应该有发现，在“7.2.3 支持向量”开头第一句话有说到“对应于α>0的样本点
        #(xi, yi)的实例xi称为支持向量”。也就是说只有支持向量的α是大于0的，在求和式内的
        #对应的αi*yi*K(xi, xj)不为0，非支持向量的αi*yi*K(xi, xj)必为0，也就不需要参与
        #到计算中。也就是说，在g(xi)内部求和式的运算中，只需要计算α>0的部分，其余部分可
        #忽略。因为支持向量的数量是比较少的，这样可以再很大程度上节约时间
        #从另一角度看，抛掉支持向量的概念，如果α为0，αi*yi*K(xi, xj)本身也必为0，从数学
        #角度上将也可以扔掉不算
        #index获得非零α的下标，并做成列表形式方便后续遍历
        index = [i for i, alpha in enumerate(self.alpha) if alpha != 0]
        #遍历每一个非零α，i为非零α的下标
        for j in index:
            #计算g(xi)
            gxi += self.alpha[j] * self.trainLabelMat[j] * self.k[j][i]
        #求和结束后再单独加上偏置b
        gxi += self.b

        #返回
        return gxi

    def calcEi(self, i):
        '''
        计算Ei
        根据“7.4.1 两个变量二次规划的求解方法”式7.105
        :param i: E的下标
        :return:
        '''
        #计算g(xi)
        gxi = self.calc_gxi(i)
        #Ei = g(xi) - yi,直接将结果作为Ei返回
        return gxi - self.trainLabelMat[i]

    def getAlphaJ(self, E1, i):
        '''
        SMO中选择第二个变量
        :param E1: 第一个变量的E1
        :param i: 第一个变量α的下标
        :return: E2，α2的下标
        '''
        #初始化E2
        E2 = 0
        #初始化|E1-E2|为-1
        maxE1_E2 = -1
        #初始化第二个变量的下标
        maxIndex = -1

        #这一步是一个优化性的算法
        #实际上书上算法中初始时每一个Ei应当都为-yi（因为g(xi)由于初始α为0，必然为0）
        #然后每次按照书中第二步去计算不同的E2来使得|E1-E2|最大，但是时间耗费太长了
        #作者最初是全部按照书中缩写，但是本函数在需要3秒左右，所以进行了一些优化措施
        #--------------------------------------------------
        #在Ei的初始化中，由于所有α为0，所以一开始是设置Ei初始值为-yi。这里修改为与α
        #一致，初始状态所有Ei为0，在运行过程中再逐步更新
        #因此在挑选第二个变量时，只考虑更新过Ei的变量，但是存在问题
        #1.当程序刚开始运行时，所有Ei都是0，那挑谁呢？
        #   当程序检测到并没有Ei为非0时，将会使用随机函数随机挑选一个
        #2.怎么保证能和书中的方法保持一样的有效性呢？
        #   在挑选第一个变量时是有一个大循环的，它能保证遍历到每一个xi，并更新xi的值，
        #在程序运行后期后其实绝大部分Ei都已经更新完毕了。下方优化算法只不过是在程序运行
        #的前半程进行了时间的加速，在程序后期其实与未优化的情况无异
        #------------------------------------------------------

        #获得Ei非0的对应索引组成的列表，列表内容为非0Ei的下标i
        nozeroE = [i for i, Ei in enumerate(self.E) if Ei != 0]
        #对每个非零Ei的下标i进行遍历
        for j in nozeroE:
            #计算E2
            E2_tmp = self.calcEi(j)
            #如果|E1-E2|大于目前最大值
            if math.fabs(E1 - E2_tmp) > maxE1_E2:
                #更新最大值
                maxE1_E2 = math.fabs(E1 - E2_tmp)
                #更新最大值E2
                E2 = E2_tmp
                #更新最大值E2的索引j
                maxIndex = j
        #如果列表中没有非0元素了（对应程序最开始运行时的情况）
        if maxIndex == -1:
            maxIndex = i
            while maxIndex == i:
                #获得随机数，如果随机数与第一个变量的下标i一致则重新随机
                maxIndex = int(random.uniform(0, self.m))
            #获得E2
            E2 = self.calcEi(maxIndex)

        #返回第二个变量的E2值以及其索引
        return E2, maxIndex

    def train(self, iter = 100):
        #iterStep：迭代次数，超过设置次数还未收敛则强制停止
        #parameterChanged：单次迭代中有参数改变则增加1
        iterStep = 0; parameterChanged = 1

        #如果没有达到限制的迭代次数以及上次迭代中有参数改变则继续迭代
        #parameterChanged==0时表示上次迭代没有参数改变，如果遍历了一遍都没有参数改变，说明
        #达到了收敛状态，可以停止了
        while (iterStep < iter) and (parameterChanged > 0):
            #打印当前迭代轮数
            print('iter:%d:%d'%( iterStep, iter))
            #迭代步数加1
            iterStep += 1
            #新的一轮将参数改变标志位重新置0
            parameterChanged = 0

            #大循环遍历所有样本，用于找SMO中第一个变量
            for i in range(self.m):
                #查看第一个遍历是否满足KKT条件，如果不满足则作为SMO中第一个变量从而进行优化
                if self.isSatisfyKKT(i) == False:
                    #如果下标为i的α不满足KKT条件，则进行优化

                    #第一个变量α的下标i已经确定，接下来按照“7.4.2 变量的选择方法”第二步
                    #选择变量2。由于变量2的选择中涉及到|E1 - E2|，因此先计算E1
                    E1 = self.calcEi(i)

                    #选择第2个变量
                    E2, j = self.getAlphaJ(E1, i)

                    #参考“7.4.1两个变量二次规划的求解方法” P126 下半部分
                    #获得两个变量的标签
                    y1 = self.trainLabelMat[i]
                    y2 = self.trainLabelMat[j]
                    #复制α值作为old值
                    alphaOld_1 = self.alpha[i]
                    alphaOld_2 = self.alpha[j]
                    #依据标签是否一致来生成不同的L和H
                    if y1 != y2:
                        L = max(0, alphaOld_2 - alphaOld_1)
                        H = min(self.C, self.C + alphaOld_2 - alphaOld_1)
                    else:
                        L = max(0, alphaOld_2 + alphaOld_1 - self.C)
                        H = min(self.C, alphaOld_2 + alphaOld_1)
                    #如果两者相等，说明该变量无法再优化，直接跳到下一次循环
                    if L == H:   continue

                    #计算α的新值
                    #依据“7.4.1两个变量二次规划的求解方法”式7.106更新α2值
                    #先获得几个k值，用来计算事7.106中的分母η
                    k11 = self.k[i][i]
                    k22 = self.k[j][j]
                    k21 = self.k[j][i]
                    k12 = self.k[i][j]
                    #依据式7.106更新α2，该α2还未经剪切
                    alphaNew_2 = alphaOld_2 + y2 * (E1 - E2) / (k11 + k22 - 2 * k12)
                    #剪切α2
                    if alphaNew_2 < L: alphaNew_2 = L
                    elif alphaNew_2 > H: alphaNew_2 = H
                    #更新α1，依据式7.109
                    alphaNew_1 = alphaOld_1 + y1 * y2 * (alphaOld_2 - alphaNew_2)

                    #依据“7.4.2 变量的选择方法”第三步式7.115和7.116计算b1和b2
                    b1New = -1 * E1 - y1 * k11 * (alphaNew_1 - alphaOld_1) \
                            - y2 * k21 * (alphaNew_2 - alphaOld_2) + self.b
                    b2New = -1 * E2 - y1 * k12 * (alphaNew_1 - alphaOld_1) \
                            - y2 * k22 * (alphaNew_2 - alphaOld_2) + self.b

                    #依据α1和α2的值范围确定新b
                    if (alphaNew_1 > 0) and (alphaNew_1 < self.C):
                        bNew = b1New
                    elif (alphaNew_2 > 0) and (alphaNew_2 < self.C):
                        bNew = b2New
                    else:
                        bNew = (b1New + b2New) / 2

                    #将更新后的各类值写入，进行更新
                    self.alpha[i] = alphaNew_1
                    self.alpha[j] = alphaNew_2
                    self.b = bNew

                    self.E[i] = self.calcEi(i)
                    self.E[j] = self.calcEi(j)

                    #如果α2的改变量过于小，就认为该参数未改变，不增加parameterChanged值
                    #反之则自增1
                    if math.fabs(alphaNew_2 - alphaOld_2) >= 0.00001:
                        parameterChanged += 1

                #打印迭代轮数，i值，该迭代轮数修改α数目
                print("iter: %d i:%d, pairs changed %d" % (iterStep, i, parameterChanged))

        #全部计算结束后，重新遍历一遍α，查找里面的支持向量
        for i in range(self.m):
            #如果α>0，说明是支持向量
            if self.alpha[i] > 0:
                #将支持向量的索引保存起来
                self.supportVecIndex.append(i)

    def calcSinglKernel(self, x1, x2):
        '''
        单独计算核函数
        :param x1:向量1
        :param x2: 向量2
        :return: 核函数结果
        '''
        #按照“7.3.3 常用核函数”式7.90计算高斯核
        result = (x1 - x2) * (x1 - x2).T
        result = np.exp(-1 * result / (2 * self.sigma ** 2))
        #返回结果
        return np.exp(result)


    def predict(self, x):
        '''
        对样本的标签进行预测
        公式依据“7.3.4 非线性支持向量分类机”中的式7.94
        :param x: 要预测的样本x
        :return: 预测结果
        '''

        result = 0
        for i in self.supportVecIndex:
            #遍历所有支持向量，计算求和式
            #如果是非支持向量，求和子式必为0，没有必须进行计算
            #这也是为什么在SVM最后只有支持向量起作用
            #------------------
            #先单独将核函数计算出来
            tmp = self.calcSinglKernel(self.trainDataMat[i, :], np.mat(x))
            #对每一项子式进行求和，最终计算得到求和项的值
            result += self.alpha[i] * self.trainLabelMat[i] * tmp
        #求和项计算结束后加上偏置b
        result += self.b
        #使用sign函数返回预测结果
        return np.sign(result)



    def test(self, testDataList, testLabelList):
        '''
        测试
        :param testDataList:测试数据集
        :param testLabelList: 测试标签集
        :return: 正确率
        '''
        #错误计数值
        errorCnt = 0
        #遍历测试集所有样本
        for i in range(len(testDataList)):
            #打印目前进度
            print('test:%d:%d'%(i, len(testDataList)))
            #获取预测结果
            result = self.predict(testDataList[i])
            #如果预测与标签不一致，错误计数值加一
            if result != testLabelList[i]:
                errorCnt += 1
        #返回正确率
        return 1 - errorCnt / len(testDataList)




if __name__ == '__main__':
    start = time.time()

    # 获取训练集及标签
    print('start read transSet')
    trainDataList, trainLabelList = loadData('../Mnist/mnist_train.csv')

    # 获取测试集及标签
    print('start read testSet')
    testDataList, testLabelList = loadData('../Mnist/mnist_test.csv')

    #初始化SVM类
    print('start init SVM')
    svm = SVM(trainDataList[:1000], trainLabelList[:1000], 10, 200, 0.001)

    # 开始训练
    print('start to train')
    svm.train()

    # 开始测试
    print('start to test')
    accuracy = svm.test(testDataList[:100], testLabelList[:100])
    print('the accuracy is:%d'%(accuracy * 100), '%')

    # 打印时间
    print('time span:', time.time() - start)