一,算法原理
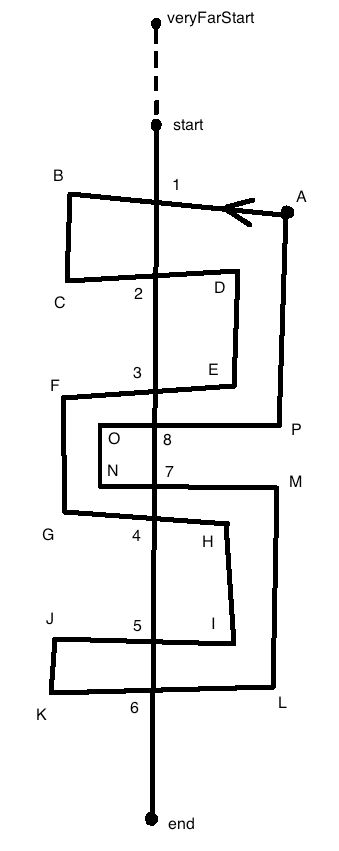
以上图为例,直线(start,end)切割凹多边形ABCDEFGHIJKLMNOP。
记
切割线divLine=(start,end)。
多边形顶点序列vertexList=(A,B,C,D,E,F,G,H,I,J,K,L,M,N,O,P)。
边序列edgeList=(AB,BC,CD,DE,EF,FG,GH,HI,IJ,JK,KL,LM,MN,NO,OP,PA)。
下面开始计算:
1,求切割点。
遍历edgeList,拿其中各edge与divLine求交,得切割点序列divPointList=(1,2,3,4,5,6,7,8)。
注:线段与直线求交,见:http://www.cnblogs.com/wantnon/p/6384543.html
插入切割点后顶点序列vertexList_afterDiv=(A,1,B,C,2,D,E,3,F,G,4,H,I,5,J,K,6,L,M,7,N,O,8,P)。
插入切割点后的边序列edgeList_afterDiv=(A1,1B,BC,C2,2D,DE,E3,3F,FG,G4,4H,HI,I5,5J,JK,K6,6L,LM,M7,7N,NO,O8,8P,PA)。
2,求各边在切割线哪一侧。
所谓“点在切割线左侧”是指:当站在start面朝end时,点在左手边。
可以使用点到直线的带符号距离来判断点在直线的哪一侧,参考:http://www.cnblogs.com/wantnon/p/6384543.html
求得结果为:B,C,F,G,J,K,N,O在切割线右侧,A,D,E,H,I,L,M,P在切割线左侧。
则切割后的边集edgeList_afterDiv被划分为两个集合:
右侧边集合:rightSideEdgeSet={1B,BC,C2,3F,FG,G4,5J,JK,K6,7N,NO,O8}。
左侧边集合:leftSideEdgeSet={A1,2D,DE,E3,4H,HI,I5,6L,LM,M7,8P,PA}。
3,求封口边。
将divLine反向延长得到点veryFarStart,我们假定点veryFarStart足够远,以至于divPointList中的所有点都在射线[veryFarStart,end)上。
然后我们根据到veryFarStart的距离对divPointList中的点进行排序,得到divPointList_sorted=(1,2,3,8,7,4,5,6)。
然后把divPointList_sorted中的点相邻两个结对儿,得到12,38,74,56。可以发现规律:
线段12,线段38,线段74,线段56,正好都是左侧子多边形的封口。
而将上面每个线段都反向,得到:线段21,线段83,线段47,线段65,正好都是右侧子多边形的封口。
所以有:
leftSideCapSet={12,38,74,56},
rightSideCapList={21,83,47,65}。
4,重新组装。
右侧边和封口形成的集合为rightSideEdgeAndCapSet=rightSideEdgeSet与rightSideCapSet的并集={1B,BC,C2,3F,FG,G4,5J,JK,K6,7N,NO,O8,21,83,47,65},
左侧边和封口形成的集合为leftSideEdgeAndCapSet=leftSideEdgeSet与leftSideCapSet的并集={A1,2D,DE,E3,4H,HI,I5,6L,LM,M7,8P,PA,12,38,74,56}。
对rightSideEdgeAndCapSet中的边进行组装,可得多边形:1BC2,3FG47NO8,5JK6,
对leftSideEdgeAndCapSet中的边形行组装,可得多边形:A12DE38P,4HI56LM7
(注意,组装过程并不需要比较坐标(比较坐标的方法不但效率低,而且特殊情况还有可能产生错误),只需对线段端点字母进行匹配即可)。
所以凹多边形ABCDEFGHIJKLMNOP被直线(start,end)切割成五个子多边形:1BC2,3FG47NO8,5JK6,A12DE38P,4HI56LM7。
计算完毕。
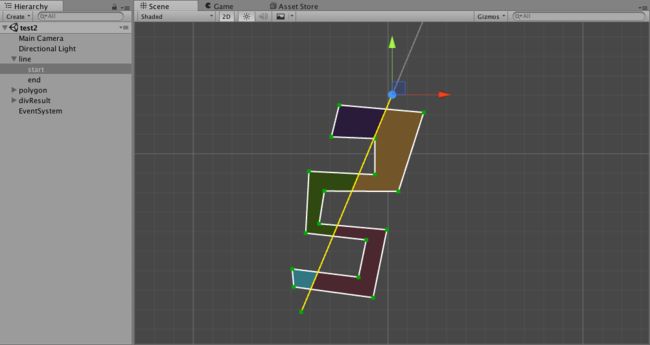
二,实现
在unity里进行了试验,效果如下:
开源地址:http://git.oschina.net/wantnon2/polygonDiv