《空间谱估计理论与算法》学习笔记004-空间谱估计基础知识

2.4 空间谱估计基础知识

2.4.1 阵列的方向图

概念：阵列输出的绝对值与来波方向之间的关系称为天线的方向图。
分类：阵列输出的直接相加（不考虑信号及其来向），即静态方向图；带指向的方向图（考虑信号指向），信号的指向是通过控制加权的相位来实现的。
根据信号模型，对于某一确定的$m$元空间阵列，在忽略噪声的条件下，第$l$个阵元的复振幅为
$$x_l=g_0{e}^{-j\omega {\tau }_l},l=1,2,\cdots ,m$$

式中$g_0$为来波的复振幅，${\tau }_l$为第$l$个阵元与参考点之间的延迟。设第$l$个阵元的权值为${\omega }_l$，那么所有阵元加权的输出相加得到阵列的输出为
$$Y_0=\sum _{l=1}^m{\omega }_l{g}_0{e}^{-j\omega {\tau }_l},l=1,2,\cdots ,m$$

对上式取绝对值并归一化后可得到空间阵列的方向图$G(\theta )$为
$$G(\theta )=\frac{|Y_0|}{\max \left\{|Y_0|\right\}}$$

若式中${\omega }_l=1(l=1,2,\cdots ,m)$，上式为静态方向图$G_0(\theta )$。
下面考虑空间谱估计中经常碰到的几种阵列的方向图：
1.均匀线阵
假设均匀线阵的间距为$d$，且以最左边的阵元为参考点（位于原点），另假设信号入射方位角为$\theta$，其中方位角表示与线阵法线方向的夹角，则
$${\tau }_l=\frac{1}{c}(x_k\sin \theta )=\frac{1}{c}(l-1)d\sin \theta$$

$$Y_0=\sum _{l=1}^m{\omega }_l{g}_0{e}^{-j\omega {\tau }_l}=\sum _{l=1}^m{\omega }_l{g}_0{e}^{-j\frac{2\pi }{\lambda }(l-1)d\sin \theta }=\sum _{l=1}^m{\omega }_l{g}_0{e}^{-j(l-1)\beta }$$

式中$\beta =\frac{2\pi d\sin \theta }{\lambda }$，$\lambda$为入射信号的波长。若式中${\omega }_l=1(l=1,2,\cdots ,m)$，上式可简化为
$$Y_0=m{g}_0{e}^{-j(m-l)\beta /2}\frac{\sin (m\beta /2)}{m\sin (\beta /2)}$$

可得均匀线阵的静态方向图
$$G_0(\theta )=\left|\frac{\sin (m\beta /2)}{m\sin (\beta /2)}\right|$$

当式中${\omega }_l=e^{j(l-1){\beta }_d}$，${\beta }_d=\frac{2\pi d\sin {\theta }_d}{\lambda }(l=1,2,\cdots ,m)$时，可简化为
$$Y_0=m{g}_0{e}^{-j(m-1)(\beta -{\beta }_d)/2}\frac{\sin [m(\beta -{\beta }_d)/2]}{m\sin [(\beta -{\beta }_d)/2]}$$

可得指向为${\theta }_d$的阵列方向图
$$G(\theta )=\left|\frac{\sin [m(\beta -{\beta }_d)/2]}{m\sin [(\beta -{\beta }_d)/2]}\right|$$

因此，静态方向图其实就是指向为${\theta }_d=0^{\circ }$时的阵列方向图。正是因为${\theta }_d=0^{\circ }$，有${\beta }_d=0$，即${\omega }_l=e^{-j(l-1){\beta }_d}=1$。
下图为16阵元的均匀线阵的方向图，阵元间距为半波长，（a）为静态方向图，（b）为指向为$30^{\circ }$的方向图，另外加了旁瓣电平为-30dB的切比雪夫权。

2.平面阵
假设平面阵是在水平面仿制的矩形阵，由$m\times n$个阵元组成，几何关系如图所示。

以阵列的左上角的阵元为参考点，$x$轴上有$n$个间距为$d$的均匀线阵，$y$轴上有$m$个间距为$d$的均匀线阵，另假设信号入射方位角为$\theta$，俯仰角为$\phi$，其中方位角表示与$x$轴夹角。则信号入射到第$k$个阵元上引起的与参考阵元间的时延为
$${\tau }_k=\frac{1}{c}(x_k\cos \theta \cos \phi +y_k\sin \theta \cos \phi )$$

若平面阵竖立放置在$xz$平面，则信号入射到第$k$个阵元上引起的与参考阵元间的时延$（y=0）$为
$${\tau }_k=\frac{1}{c}(x_k\cos \theta \cos \phi +z_k\sin \phi )$$

因此，${\omega }_i=1$，$g_0=1$时的水平面放置的平面阵的方向图为
$$\begin{array}{rl}G(\theta )& =\sum _{i=1}^{mn}{g}_0{e}^{-j(x_i\cos \theta \cos \phi +y_i\sin \theta \cos \phi )\frac{2\pi }{\lambda }}\\ & =\sum _{i=1}^m\sum _{k=1}^n{e}^{-j(i-1)\frac{2\pi d}{\lambda }\cos \theta \cos \phi }{e}^{-j(k-1)\frac{2\pi d}{\lambda }\sin \theta \cos \phi }\\ & =\sum _{i=1}^m{e}^{-j(i-1)\frac{2\pi d}{\lambda }\cos \theta \cos \phi }\sum _{k=1}^n{e}^{-j(k-1)\frac{2\pi d}{\lambda }\sin \theta \cos \phi }\\ & =G_{row}(\theta )G_{col}(\theta )\end{array}$$

即平面阵的方向图相当于合成行子阵（平行于$x$方向）方向图$G_{row}(\theta )$与合成列子阵（平行于$y$方向）方向图$G_{col}(\theta )$的乘积。
${\omega }_i=1$，$g_0=1$时的竖面放置的平面阵的方向图为
$$\begin{array}{rl}G(\theta )& =\sum _{i=1}^{mn}{g}_0{e}^{-j(x_i\cos \theta \cos \phi +z_i\sin \phi )\frac{2\pi }{\lambda }}\\ & =\sum _{i=1}^m\sum _{k=1}^n{e}^{-j(i-1)\frac{2\pi d}{\lambda }\cos \theta \cos \phi }{e}^{-j(k-1)\frac{2\pi d}{\lambda }\sin \phi }\\ & =G_{row}(\theta )G_{col}(\theta )\end{array}$$

即竖面放置平面阵的方向图相当于合成行子阵（平行于$x$方向）方向图$G_{row}(\theta )$与合成列子阵（平行于$y$方向）方向图$G_{col}(\theta )$的乘积。
3.均匀圆阵
假设均匀圆阵由$m$个阵元组成，以圆心为参考点，设半径为$r$。如果圆阵水平放置，则信号入射到第$k$个阵元上引起的与参考阵元间的时延（$z=0$）为
$${\tau }_k=\frac{1}{c}(x_k\cos \theta \cos \phi +z_k\sin \phi )$$

${\omega }_i=1$，$g_0=1$时的方向图为
$$\begin{array}{rl}G(\theta )& =\sum _{k=1}^m{e}^{-j(x_k\cos \theta \cos \phi +y_k\sin \theta \cos \phi )\frac{2\pi }{\lambda }}\\ & =\sum _{k=1}^m{e}^{-j\frac{r}{c}\cos (2\pi (k-1)/m-\theta )\cos \phi }\end{array}$$

如果圆阵竖立放置，则信号入射到第$k$个阵元上引起的与参考阵元间的时延（$y=0$）为
$${\tau }_k=\frac{1}{c}(x_k\cos \theta \cos \phi +y_k\sin \theta \cos \phi )$$

${\omega }_i=1$，$g_0=1$时的方向图为
$$G(\theta )=\sum _{k=1}^{mn}{e}^{-j(x_k\cos \theta \cos \phi +z_k\sin \phi )\frac{2\pi }{\lambda }}$$

2.4.2 基本原理

基本原理：对于一般的远场信号而言，同一信号到达不同的阵元存在一个波程差，这个波程差导致了各接收阵元间的相位差，利用各阵元间的相位差可估计出信号的方位。

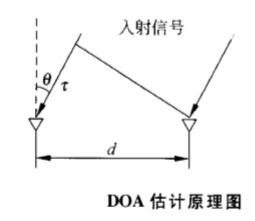
上图中考虑两个阵元，$d$为阵元间的间距，$c$为光速，$\theta$为远场信号的入射角，$\psi$为阵元间的相位延迟。则天线所接收信号由于波程差
$$\tau =\frac{d\sin \theta }{c}$$

可得两阵元间的相位差
$$\psi =e^{-j\omega \tau }=e^{-j\omega \frac{d\sin \theta }{c}}=e^{-j2\pi \frac{d\sin \theta }{\lambda f_0}f}$$

$\lambda$为信号波长，$f_0$为中心频率。对于窄带信号，相位差
$$\psi =e^{-j2\pi \frac{d\sin \theta }{\lambda }}$$

因此，只要知道信号的相位延迟就可得出信号的来向。
一般情况下，对于空间的任意两个阵元而言，波程差应为
$$\tau =\frac{1}{c}(x\cos \theta \cos \phi +y\sin \theta \cos \phi +z\sin \phi )$$

因此，只要知道空间阵元间的相位差，就可以估计入射信号的方位角、俯仰角等信号参数。

2.4.3 波束宽度

DOA估计中，线阵的侧向范围为$[-90^{\circ },90^{\circ }]$，而一般的面阵如圆阵的侧向范围为$[-180^{\circ },180^{\circ }]$。为了说明波束宽度，下面只考虑线阵，$m$个阵元的均匀线阵的静态方向图为
$$G_0(\theta )=\left|\frac{\sin (m\beta /2)}{m\sin (\beta /2)}\right|$$

式中，空间频率
$$\beta =\frac{2\pi d\sin \theta }{\lambda }$$

则对于天线静态方向图主瓣的零点，由$|G_0(\theta ){|}^2=0$可得零点波束宽度$B{W}_0$为
$$B{W}_0=2\arcsin \lambda /md$$

而由$|G_0(\theta ){|}^2=1/2$，可得到半功率点波束宽度$B{W}_{0.5}$，在$md\gg \lambda$的条件下有
$$B{W}_{0.5}\approx 0.886\lambda /md$$

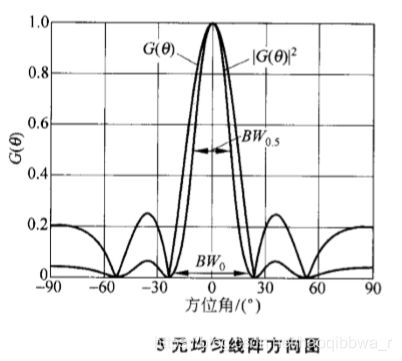
上图时5元均匀线阵的方向图，阵元间距为半波长。
一般考虑静态方向图的半功率点波束宽度，即对于均匀线阵而言，波束宽度为
$$BW\approx \frac{51^{\circ }}{D/\lambda }=\frac{0.89}{D/\lambda }\mathrm{r}\mathrm{a}\mathrm{d}$$

$D$为天线的有效孔径，$\lambda$为信号波长，$\mathrm{r}\mathrm{a}\mathrm{d}$表示弧度单位。对于$m$阵元的等距均匀线阵，阵元间距为$\lambda /2$，则天线的有效孔径为$D=(m-1)\lambda /2$，对于ULA阵，阵列的波束宽度近似计算公式为
$$BW\approx \frac{102^{\circ }}{m}$$

关于波束宽度，要注意：
（1）波束宽度与天线孔径成反比，一般情况下天线的半功率点波束宽度与天线孔径之间有如下关系
$$B{W}_{0.5}\approx (40\sim 60)\frac{\lambda }{D}$$

（2）对于某些阵列，天线的波束宽度与波束的指向有关系，如波束指向为${\theta }_d$时，均匀线阵的波束宽度为
$$B{W}_0=\arcsin (\frac{\lambda }{md}+\sin {\theta }_d)$$

$$B{W}_{0.5}\approx 0.886\frac{\lambda }{md}\cdot \frac{1}{\cos {\theta }_d}$$

（3）波束宽度越窄，阵列的指向性越好，也就是说明阵列分辨空间信号的能力越强。

2.4.4 分辨力

阵列测向中，在某方向上对信源的分辨力与在该方向附近阵列方向矢量的变化率直接相关。在方向矢量变化较快的方向附近，随信源角度变化阵列快排数据变化大，相应的分辨力就高。定义一个表征分辨力的量$D(\theta )$
$$D(\theta )=\Vert \frac{\mathrm{d}a\text{a}a(\theta )}{\mathrm{d}\theta }\Vert \propto \Vert \frac{\mathrm{d}\tau }{\mathrm{d}\theta }\Vert$$

$D(\theta )$越大表明在该方向上的分辨力越高。
对于均匀线阵
$${\tau }_l=\frac{1}{c}(x_k\sin \theta )=\frac{1}{c}(l-1)d\sin \theta$$

则
$$D(\theta )\propto \cos \theta$$

说明信号在$0^{\circ }$方向分辨率最高，而在$60^{\circ }$分辨力已降了一半，所以一般线阵的测向范围为$-60^{\circ }\sim 60^{\circ }$。
对于水平放置的均匀圆阵，令$\psi =0$，可得
$$\begin{array}{rl}{\tau }_k& =\frac{1}{c}(x_k\cos \theta +y_k\sin \theta )\\ & =\frac{r}{c}\cos (\frac{2\pi (k-1)}{m-\theta })\end{array}$$

则
$$D(\theta )\propto {\left|\frac{\mathrm{d}\tau }{\mathrm{d}\theta }\right|}_F=\frac{r}{c}\sqrt{\frac{m}{2}}$$

说明对于水平放置的均匀圆阵，其分辨力是一个与阵列孔径及阵元数有关的常数。

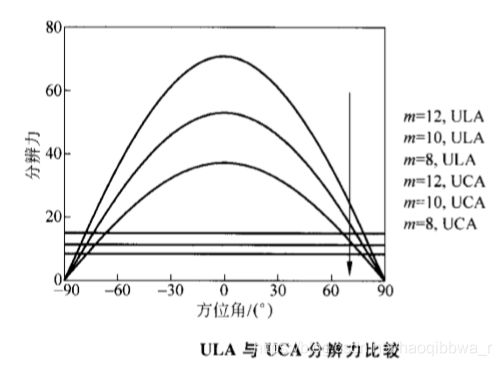
上图是关于均匀线阵（ULA）与均匀圆阵（UCA）两个阵列的分辨力比较，其中阵列阵元间的间距均为半波长，$m$表示阵元数。可以看出，在阵元间距固定的情况下，阵列的分辨力随着阵元数的增加而变好，即与阵列孔径成正比；一般情况下线阵的分辨力好于圆阵。
在空间谱估计技术中大部分算法涉及谱峰搜索，比如为了估计入射信号的方位角，就必须通过搜索阵列的整个视角得到角度谱$\hat{P}(\theta )$，这样$\hat{P}(\theta )$几个极大值点对应的角度就是信号的入射方向。在谱峰搜索的算法中分辨力的界限可定义为两个入射信号角度均值的谱峰，即
$$E[\hat{P}({\theta }_m)]=E[\frac{\hat{P}({\theta }_1)+\hat{P}({\theta }_2)}{2}]$$

式中，${\theta }_m=({\theta }_1+{\theta }_2)/2$。按上式的分辨力界限的定义即当等式左边小于右边时，两个角度是可分辨的，当左边大于右边时，说明两个相近的角度是不可分辨的。

2.4.5 空时等效性

对于空间阵列中按位置放置的一系列阵元，在窄带远场信号的假设下，任两阵元接收信号的时间差为
$${\tau }_s=\frac{d\sin \theta }{c}=\frac{k\lambda \sin \theta }{c}=\frac{k\sin \theta }{f}$$

式中，$k=0.5$，表示阵列阵元间距为半波长，$d$为阵元间距。时域处理中各采样点之间的时间差即采样间隔
$${\tau }_T=\frac{1}{f_S}$$

式中，$f_S$为采样频率。

空域处理的时间差与角度有关（阵元的位置相当于对空间的采样），时域处理的时间差是一个常数。天线的方向图相当于时域的傅里叶变换，加权的方向图相当于时域加权的傅里叶变换。

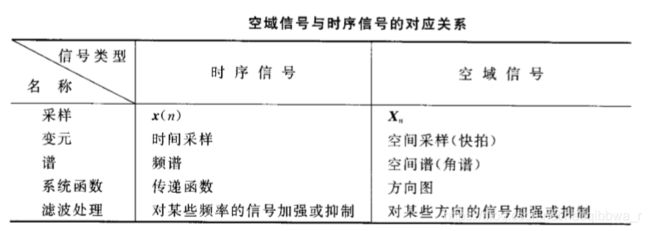
时域的分辨力正比于观察长度，空间阵列的阵元数是有限的，空域分辨力正比于阵列孔径。