leetcode刷题之树专题
文章目录
- 1. 关于层次遍历
- 2. 非递归层次遍历
-
- 2.1 N叉树的层次遍历
- 2.2 二叉树的最大宽度
- 3. 记录层次信息的递归遍历
-
- 3.1 二叉树的锯齿形层次遍历
- 3.2 二叉树的右视图
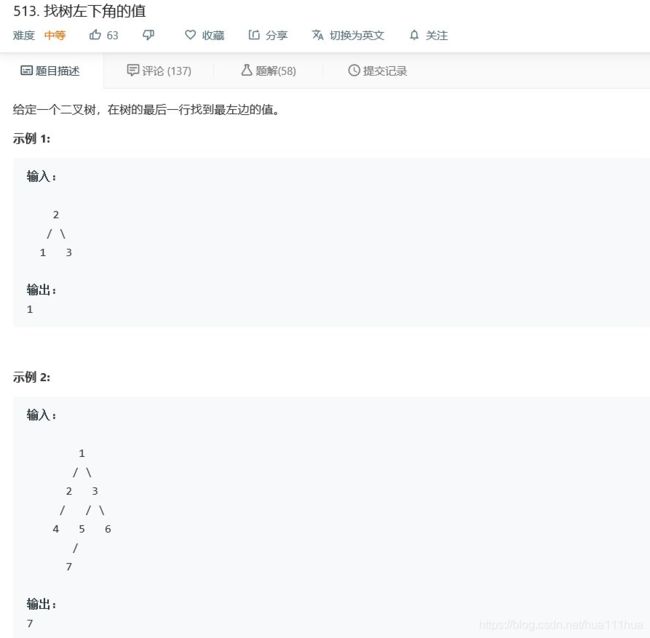
- 3.3 找树左下角的值
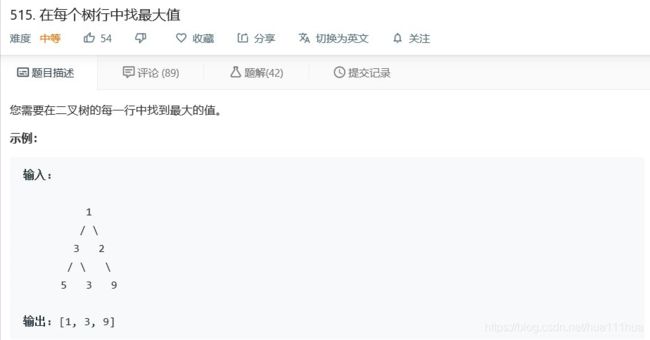
- 3.4 在每个树行中找最大值
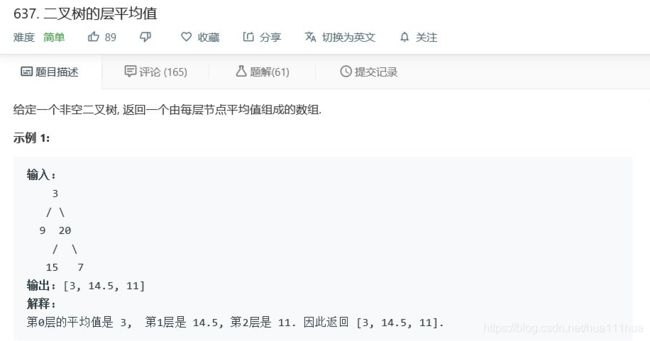
- 3.5 二叉树的层平均值
- 3.6 层数最深叶子节点的和
- 4.关于前中后遍历
-
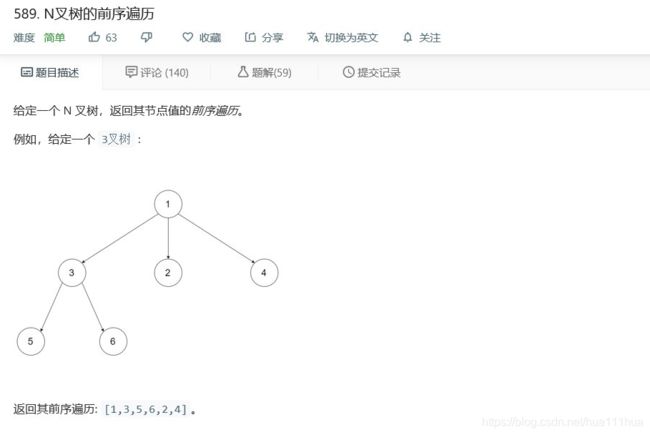
- 4.1 N叉树的前序遍历
- 4.2 N叉树的后序遍历
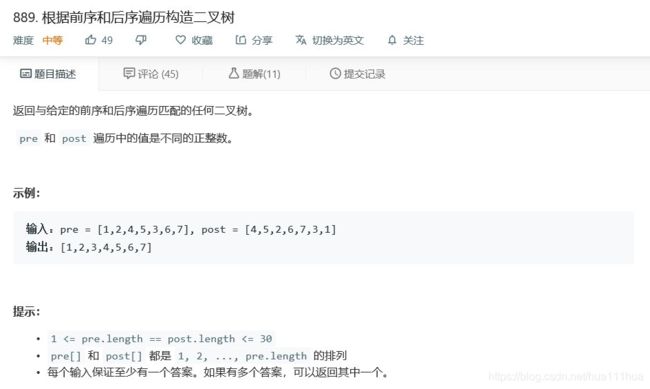
- 4.3 根据前序和后续遍历构造二叉树
- 4.4 从中序与后序遍历序列构造二叉树
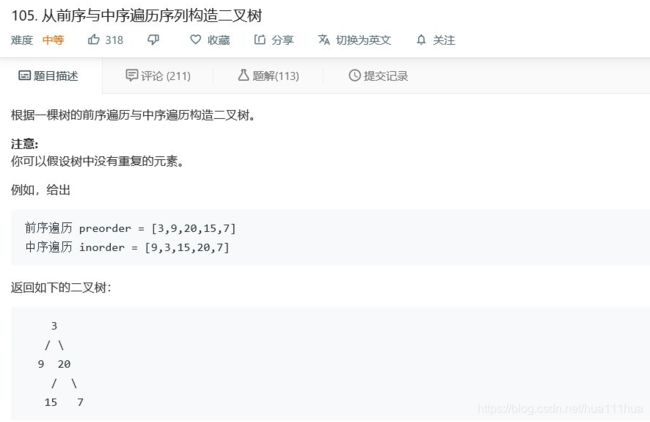
- 4.5 从前序与中序遍历序列构造二叉树
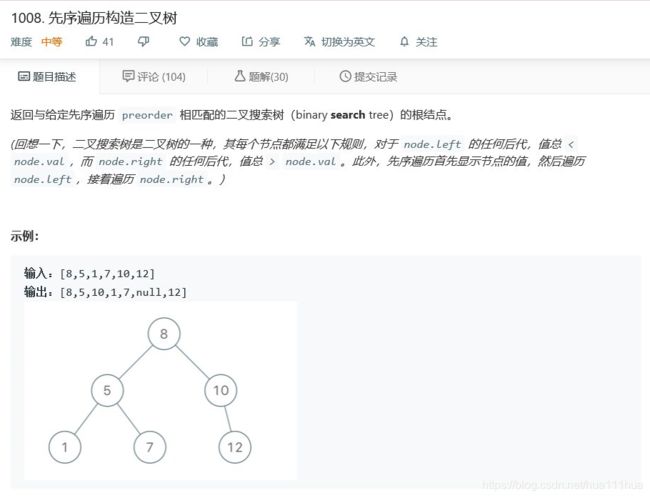
- 4.6 先序遍历构造二叉树
- 4.7 二叉树中第二小的节点
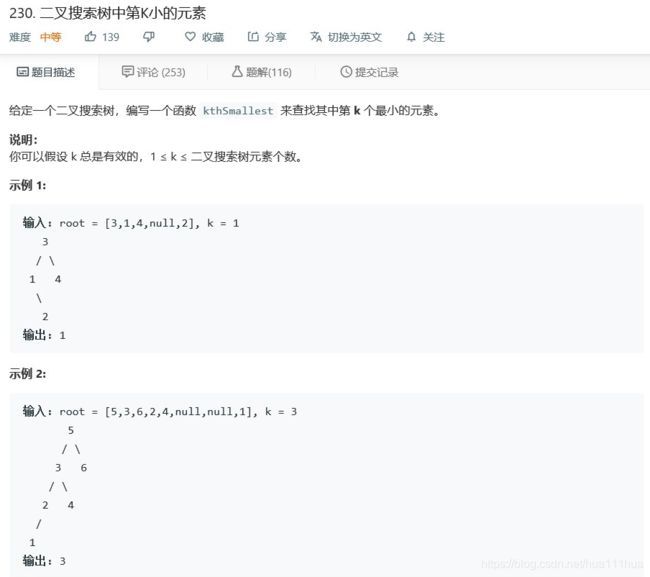
- 4.8 二叉搜索树中第K小的元素
- 5.关于树的操作与性质
-
- 5.1 二叉树剪枝
- 5.2 将有序数组转换为二叉搜索树
- 5.3 二叉树展开为链表
- 5.4 填充每个节点的下一个右侧节点指针
- 5.5 填充每个节点的下一个右侧节点指针II
- 5.6 翻转二叉树
- 5.7 序列化和反序列化二叉搜索树
- 5.8 删除二叉搜索树中的节点
- 5.9 二叉搜索树的最小绝对差
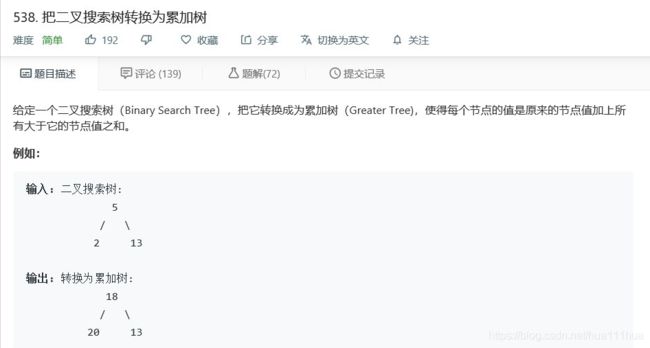
- 5.10 把二叉搜索树转换为累加树
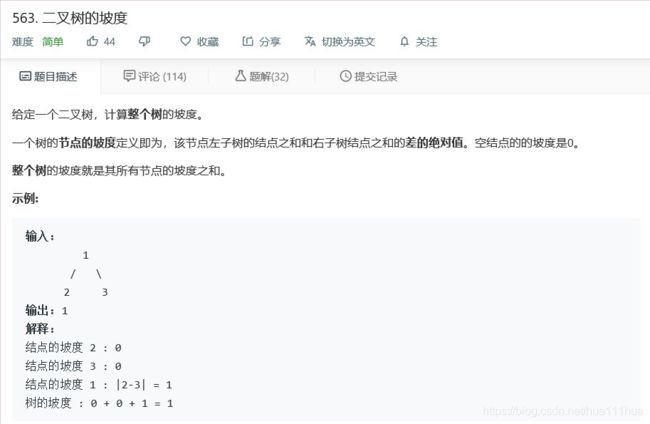
- 5.11 二叉树的坡度
- 5.12 二叉树的直径
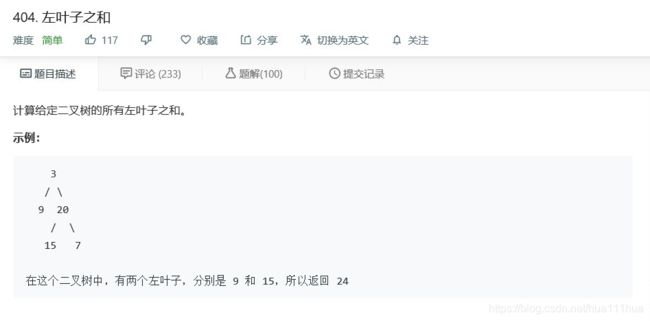
- 5.13 左叶子之和
- 5.14 修剪二叉搜索树
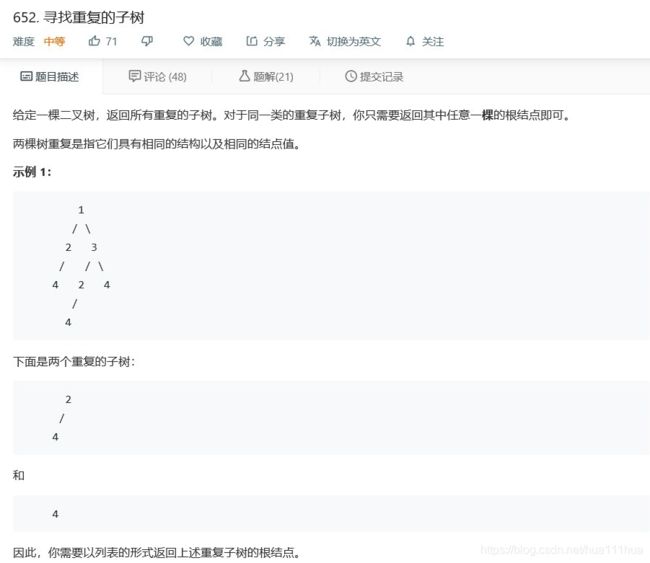
- 5.15 寻找重复的子树
- 5.16 合并二叉树
- 5.17 根据二叉树创建字符串
- 5.18 二叉搜索树中的搜索
- 5.19 二叉搜索树的范围和
- 5.19 二叉树的最小深度
- 5.20 N叉树的最大深度
- 5.21 输出二叉树
- 5.22 验证二叉搜索树
- 5.23 恢复二叉搜索树
- 5.24 二叉树的所有路径
- 5.25 二叉树的最近公共祖先
- 5.26 二叉搜索树的最近公共祖先
- 5.27出现次数最多的子树元素和
- 5.28 二叉搜索树中的众数
- 5.29 二叉树的最大深度
- 5.30 求根到叶子节点数字之和
- 6.关于特殊要求的树
-
- 6.1 叶子相似的树
- 6.2 单值二叉树
- 6.3 最大二叉树
- 6.4 平衡二叉树
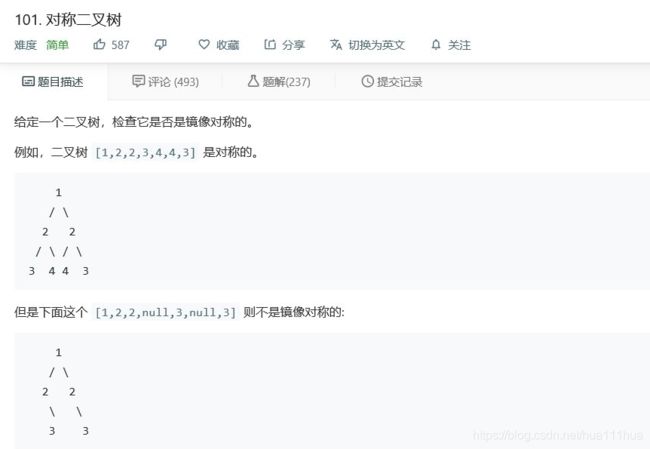
- 6.5 对称二叉树
- 6.6 两数之和IV
- 6.7 相同的树
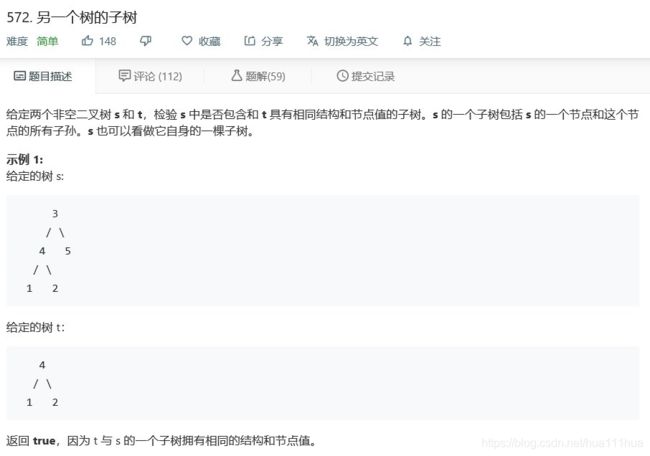
- 6.8 另一个树的子树
- 6.9 不同的二叉搜索树
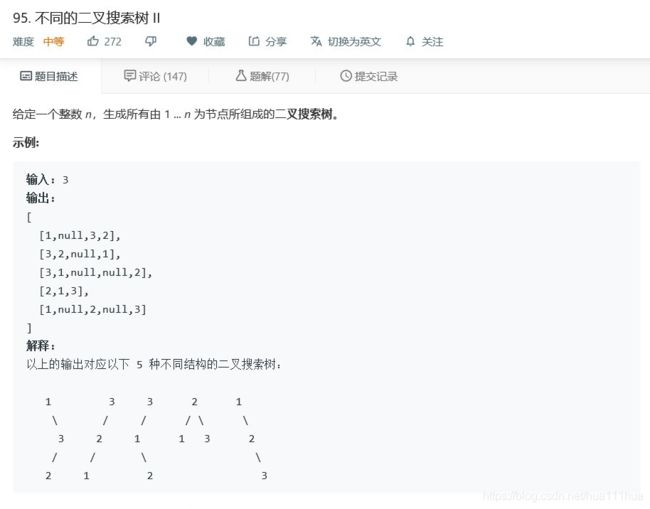
- 6.10 不同的二叉搜索树II
- 6.11 对称二叉树
- 7.关于树的应用
-
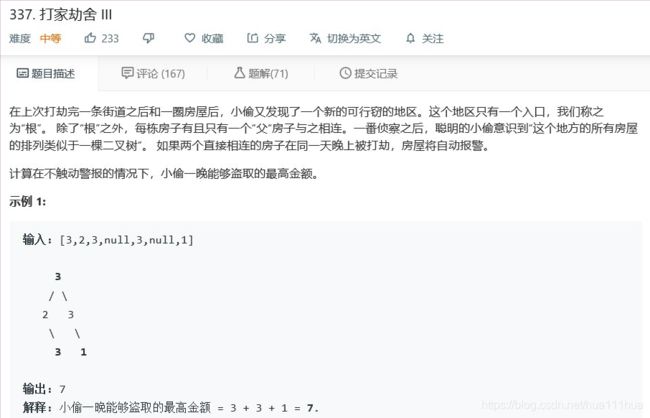
- 7.1 打家劫舍III
- 7.2 二叉树中的最大路径和
- 7.3 路径总和
- 7.4 路径总和II
- 7.5 路径总和III
1. 关于层次遍历
层次遍历在树的遍历中有着非常重要的地位,本篇博客提出两种遍历方式,一种是最基本的使用队列完成的非递归遍历,一种是遍历过程中统计遍历层数的递归遍历,这种统计层数的好处是可以记录下每层的节点信息,对于找特殊层的元素或者对层次进行特殊操作极为方便。
2. 非递归层次遍历
def levelorder(root):
res,queue=[],[root]
if not root:
return res
while queue:
node=queue.pop(0)
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
res.append(node)
return res2.1 N叉树的层次遍历

因为是多叉树,使用二叉树递归左右子树的遍历方式不太合适,所以使用非递归的迭代方式进行遍历。
def levelOrder(self, root: 'Node') :
if not root:
return []
res = []
cur = [root]
while cur:
next = []
temp = []
for node in cur:
temp.append(node.val)
next += node.children
res.append(temp)
cur = next
return res2.2 二叉树的最大宽度
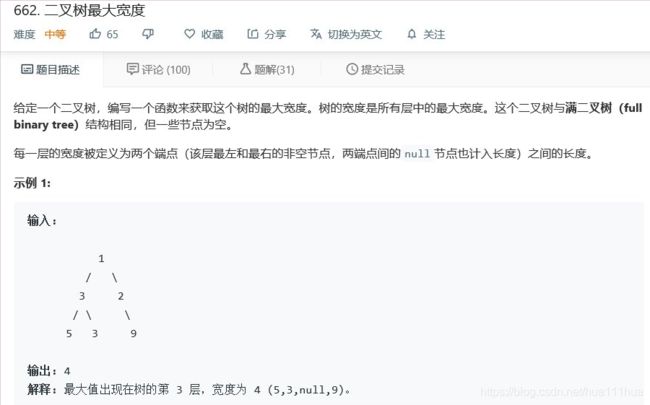
这个题的难点在于有值的两个节点之间空的节点也会被统计进去,所以需要在层次遍历的时候记录下左右节点的index,然后使用动态规划的方法得到最大的宽度值。
def widthOfBinaryTree(self, root: TreeNode) :
if not root:
return 0
queue=[]
res=0
queue.append([root,1])
while queue:
n=len(queue)
left=queue[0][1]
right=0
for i in range(n):
x=queue.pop(0)
right=x[1]
if x[0].left:
queue.append([x[0].left,right*2])
if x[0].right:
queue.append([x[0].right,right*2+1])
res=max(res,right-left+1)
return res3. 记录层次信息的递归遍历
def levelOrderBottom(self, root: TreeNode) :
res=[]
def helper(root, depth):
if not root:
return
if len(res)==depth:
res.append([])
res[depth].append(root.val)
helper(root.left,depth+1)
helper(root.right,depth+1)
helper(root,0)
return res3.1 二叉树的锯齿形层次遍历
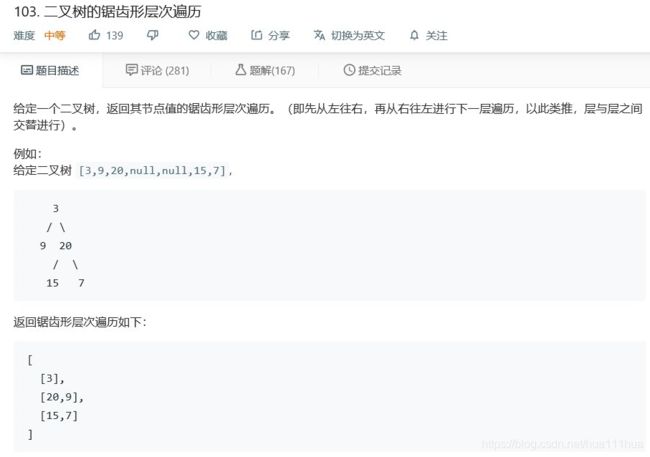
按照3的代码模板,只需要加上对depth的奇偶判断,然后调整插入元素的方向即可。
def zigzagLevelOrder(self, root: TreeNode) :
res=[]
def helper(root,depth):
if not root:
return
if len(res)==depth:
res.append([])
if depth%2==0:
res[depth].append(root.val)
else:
res[depth].insert(0,root.val)
helper(root.left,depth+1)
helper(root.right,depth+1)
helper(root,0)
return res3.2 二叉树的右视图
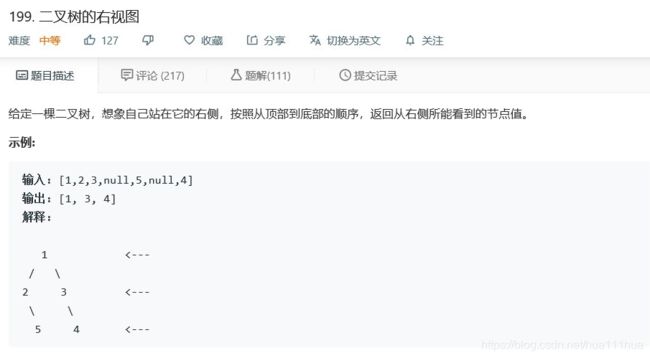
使用3的模板记录下每层的节点信息,保存成list(res),然后遍历res,取出res中的每个元素(list格式)的最后一个元素即可。(如果是左视图,就取出res中的每个元素的第一个元素即可)
def rightSideView(self, root: TreeNode) :
res=[]
def helper(root,depth):
if not root:
return res
if len(res)==depth:
res.append([])
res[depth].append(root.val)
helper(root.left,depth+1)
helper(root.right,depth+1)
helper(root,0)
num=[]
for res_each in res:
num.append(res_each[-1])
return num当然,这个题也可以直接使用非递归层次遍历去做,代码如下:
def rightSideView(self, root: TreeNode):
res=[]
if not root:
return res
queue=[root]
while queue:
new=[]
for i in queue:
if i.left:
new.append(i.left)
if i.right:
new.append(i.right)
res.append(queue[-1].val)
queue=new
return res3.3 找树左下角的值
def findBottomLeftValue(self, root: TreeNode) :
res=[]
def helper(root,depth):
if not root:
return
if len(res)==depth:
res.append([])
res[depth].append(root.val)
helper(root.left,depth+1)
helper(root.right,depth+1)
helper(root,0)
return res[-1][0]3.4 在每个树行中找最大值
def largestValues(self, root: TreeNode) :
res,num=[],[]
def helper(root,depth):
if not root:
return
if len(res)==depth:
res.append([])
res[depth].append(root.val)
helper(root.left,depth+1)
helper(root.right,depth+1)
helper(root,0)
for res_num in res:
num.append(max(res_num))
return num3.5 二叉树的层平均值
def averageOfLevels(self, root: TreeNode):
res=[]
def helper(root,depth):
if not root:
return res
if len(res)==depth:
res.append([])
res[depth].append(root.val)
helper(root.left,depth+1)
helper(root.right,depth+1)
helper(root,0)
num=[]
for res_each in res:
num.append(sum(res_each)/len(res_each))
return num3.6 层数最深叶子节点的和
def deepestLeavesSum(self, root: TreeNode) :
res=[]
def helper(root,depth):
if not root:
return res
if len(res)==depth:
res.append([])
res[depth].append(root.val)
helper(root.left,depth+1)
helper(root.right,depth+1)
helper(root,0)
return sum(res[-1])4.关于前中后遍历
关于前中后遍历可以参看博文面试基本数据结构和算法
4.1 N叉树的前序遍历
def preorder(self, root: 'Node') :
if not root:
return []
result,stack=[],[root]
while stack:
root=stack.pop()
result.append(root.val)
if root.children:
for idx in range(len(root.children)-1,-1,-1):
stack.append(root.children[idx])
return result4.2 N叉树的后序遍历
def postorder(self, root: 'Node') :
if not root:
return []
stack,res=[root],[]
while stack:
node=stack.pop()
res.append(node.val)
if node.children:
stack.extend(node.children)
return res[::-1]4.3 根据前序和后续遍历构造二叉树
def constructFromPrePost(self, pre: List[int], post: List[int]) :
if not pre:
return None
root=TreeNode(pre[0])
if len(pre)==1:
return root
n=post.index(pre[1])
root.left=self.constructFromPrePost(pre[1:n+2],post[:n+1])
root.right=self.constructFromPrePost(pre[n+2:],post[n+1:-1])
return root4.4 从中序与后序遍历序列构造二叉树
def buildTree(self, inorder: List[int], postorder: List[int]) :
if not postorder:
return None
x=postorder.pop(len(postorder)-1)
node=TreeNode(x)
i=inorder.index(x)
node.left=self.buildTree(inorder[:i],postorder[:i])
node.right=self.buildTree(inorder[i+1:],postorder[i:])
return node4.5 从前序与中序遍历序列构造二叉树
def buildTree(self, preorder: List[int], inorder: List[int]) :
if not preorder:
return None
x=preorder.pop(0)
node=TreeNode(x)
i=inorder.index(x)
node.left=self.buildTree(preorder[:i],inorder[:i])
node.right=self.buildTree(preorder[i:],inorder[i+1:])
return node4.6 先序遍历构造二叉树
def bstFromPreorder(self, preorder: List[int]) :
if not preorder:
return None
root=TreeNode(preorder[0])
left,right=[],[]
for x in preorder[1:]:
if x<root.val:
left.append(x)
else:
right.append(x)
root.left=self.bstFromPreorder(left)
root.right=self.bstFromPreorder(right)
return root4.7 二叉树中第二小的节点
def findSecondMinimumValue(self, root: TreeNode):
def inOrder(self, root:TreeNode):
res = []
if(root != None):
res = res + self.inOrder(root.left)
res.append(root.val)
res = res + self.inOrder(root.right)
return res
listNode = set(self.inOrder(root))
sortedNode = sorted(listNode)
if(len(listNode) == 1):
return -1
else:
return sortedNode[1]4.8 二叉搜索树中第K小的元素
def kthSmallest(self, root: TreeNode, k: int) :
lst =[]
def get(r):
if r is not None:
get(r.left)
lst.append(r.val)
get(r.right)
return lst
lst_n = get(root)
return lst_n[k-1]5.关于树的操作与性质
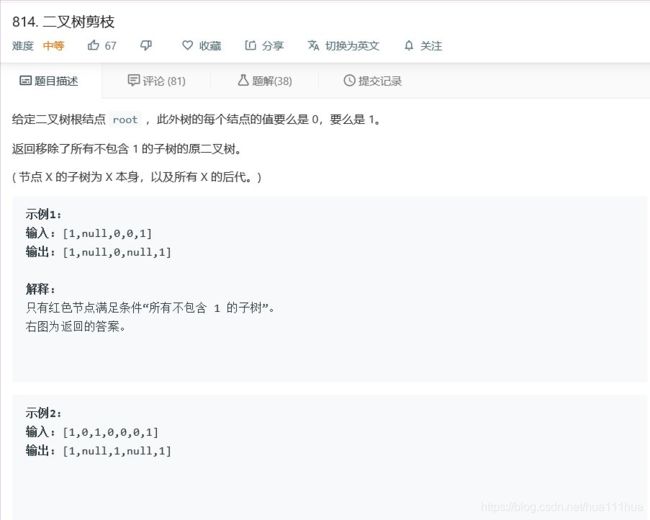
5.1 二叉树剪枝
def pruneTree(self, root: TreeNode):
if not root:
return None
root.left=self.pruneTree(root.left)
root.right=self.pruneTree(root.right)
if root.val==0 and not root.left and not root.right:
return None
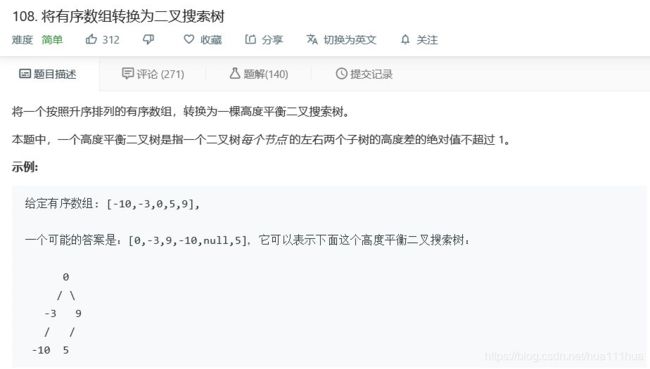
return root5.2 将有序数组转换为二叉搜索树
def sortedArrayToBST(self, nums: List[int]) :
if not nums:
return None
else:
mid=len(nums)//2
node=TreeNode(nums[mid])
node.left=self.sortedArrayToBST(nums[:mid])
node.right=self.sortedArrayToBST(nums[mid+1:])
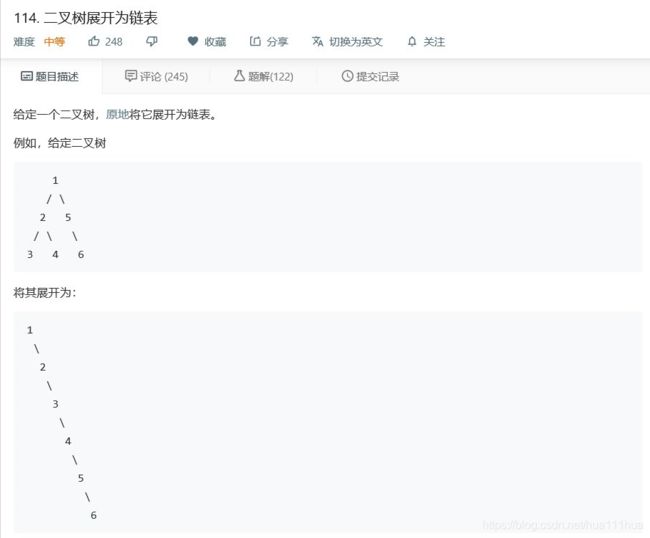
return node5.3 二叉树展开为链表
def flatten(self, root: TreeNode) :
"""
Do not return anything, modify root in-place instead.
"""
def helper(root):
if root == None: return
helper(root.left)
helper(root.right)
if root.left != None: # 后序遍历
pre = root.left # 令 pre 指向左子树
while pre.right: pre = pre.right # 找到左子树中的最右节点
pre.right = root.right # 令左子树中的最右节点的右子树 指向 根节点的右子树
root.right = root.left # 令根节点的右子树指向根节点的左子树
root.left = None # 置空根节点的左子树
root = root.right # 令当前节点指向下一个节点
helper(root)5.4 填充每个节点的下一个右侧节点指针
def connect(self, root: 'Node'):
if not root:
return
if root.left:
root.left.next = root.right
if root.next:
root.right.next = root.next.left
self.connect(root.left)
self.connect(root.right)
return root5.5 填充每个节点的下一个右侧节点指针II
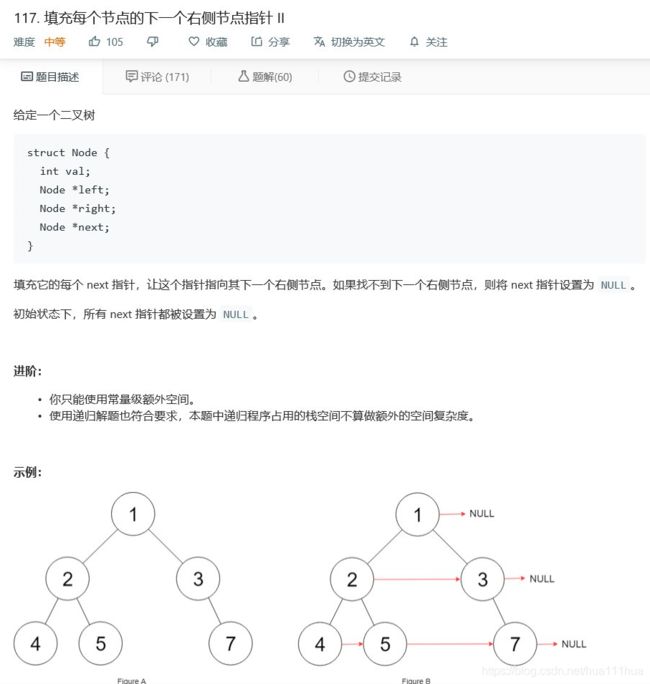

这个跟前一题的主要区别是这里的空指针也被标注出来了,所以还要加上空指针的检测和处理。
def connect(self, root: 'Node'):
if not root:
return None
queue = [root]
while queue:
next_queue = []
for i in range(len(queue)):
if queue[i].left:
next_queue.append(queue[i].left)
if queue[i].right:
next_queue.append(queue[i].right)
if i < len(queue) - 1:
queue[i].next = queue[i + 1]
queue = next_queue
return root5.6 翻转二叉树
def invertTree(self, root: TreeNode):
if not root:
return None
root.left,root.right=self.invertTree(root.right),self.invertTree(root.left)
return root5.7 序列化和反序列化二叉搜索树
def serialize(self, root: TreeNode):
#Encodes a tree to a single string.
def preorder(root):
out=[]
if root:
out+=[str(root.val)]
out+=preorder(root.left)
out+=preorder(root.right)
return out
return ','.join(preorder(root))
def deserialize(self, data: str):
#Decodes your encoded data to tree.
if not data:
return None
def buildTree(pre_o, in_o):
if not pre_o:
return None
mid = pre_o[0]
i = in_o.index(mid)
root = TreeNode(mid)
root.left = buildTree(pre_o[1:i + 1], in_o[:i])
root.right = buildTree(pre_o[i + 1:], in_o[i + 1:])
return root
pre_o = list(map(int, data.split(',')))
in_o = sorted(pre_o)
return buildTree(pre_o, in_o)5.8 删除二叉搜索树中的节点
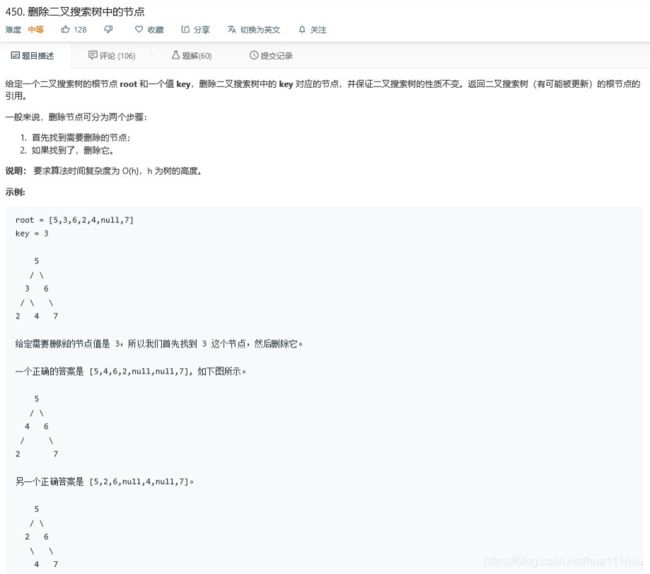
这道题的思路是找到右子树中的最小值,将要删除的节点替换为该值,然后在右子树中删除最小的那个节点。
def deleteNode(self, root: TreeNode, key: int):
if not root:
return None
if root.val>key:
root.left=self.deleteNode(root.left,key)
elif root.val<key:
root.right=self.deleteNode(root.right,key)
else:
if not root.left or not root.right:
root=root.left if root.left else root.right
else:
cur=root.right
while cur.left:
cur=cur.left
root.val=cur.val
root.right=self.deleteNode(root.right,cur.val)
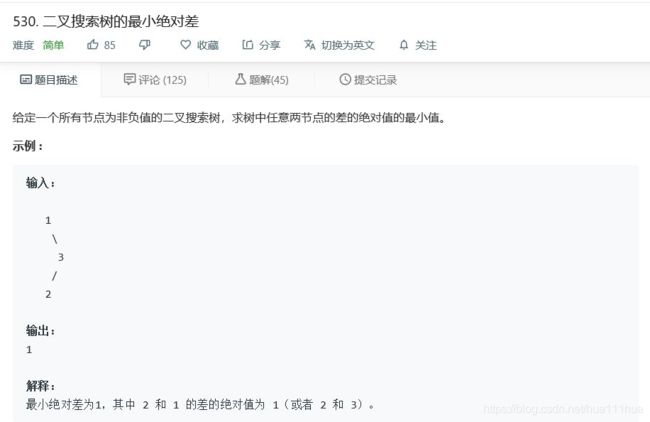
return root5.9 二叉搜索树的最小绝对差
def getMinimumDifference(self, root: TreeNode):
def inorder(node):
if not node:
return []
return inorder(node.left)+[node.val]+inorder(node.right)
res=99999999
l=inorder(root)
for i in range(1,len(l)):
res=min(res,l[i]-l[i-1])
return res5.10 把二叉搜索树转换为累加树
def convertBST(self, root: TreeNode):
def rdl(self,root,preans=0):
if root is None:
return preans
root.val+=self.rdl(root.right,preans)
return self.rdl(root.left,root.val)
rdl(root)
return root5.11 二叉树的坡度
def findTilt(self, root: TreeNode):
ret = [0]
def tile(node):
if not node:return 0
left = tile(node.left)
right = tile(node.right)
ret[0] += abs(left - right)
return left + right + node.val
tile(root)
return ret[0]5.12 二叉树的直径
def diameterOfBinaryTree(self, root: TreeNode) :
self.R=0
self.dfs(root)
return self.R
def dfs(self,root):
if not root:
return 0
l=self.dfs(root.left)
r=self.dfs(root.right)
self.R=max(l+r,self.R)
return max(l,r)+15.13 左叶子之和
def sumOfLeftLeaves(self, root: TreeNode) :
if root==None:
return 0
if root.left and root.left.left==None and root.left.right==None:
return root.left.val+self.sumOfLeftLeaves(root.right)
else:
return self.sumOfLeftLeaves(root.left)+self.sumOfLeftLeaves(root.right)5.14 修剪二叉搜索树
def trimBST(self, root: TreeNode, L: int, R: int) :
if not root:
return None
root.left = self.trimBST(root.left, L, R)
root.right = self.trimBST(root.right, L, R)
if root.val < L:
return root.right
if root.val > R:
return root.left
return root5.15 寻找重复的子树
def findDuplicateSubtrees(self, root: TreeNode):
ans, d = [], {
}
def f(r):
if not r:
return ' '
s = str(r.val) + f(r.left) + f(r.right)
if s not in d:
d[s] = True
elif d[s]:
ans.append(r)
d[s] = False
return s
f(root)
return ans5.16 合并二叉树
def mergeTrees(self, t1: TreeNode, t2: TreeNode):
if t1 and t2:
t1.val+=t2.val
t1.left=self.mergeTrees(t1.left,t2.left)
t1.right=self.mergeTrees(t1.right,t2.right)
return t1
return t1 or t25.17 根据二叉树创建字符串
def tree2str(self, t: TreeNode):
if not t:
return ""
if not t.left and not t.right:
return str(t.val)
result=str(t.val)
if t.left:
result+="("+self.tree2str(t.left)+")"
else:
result+="()"
if t.right:
result+="("+self.tree2str(t.right)+")"
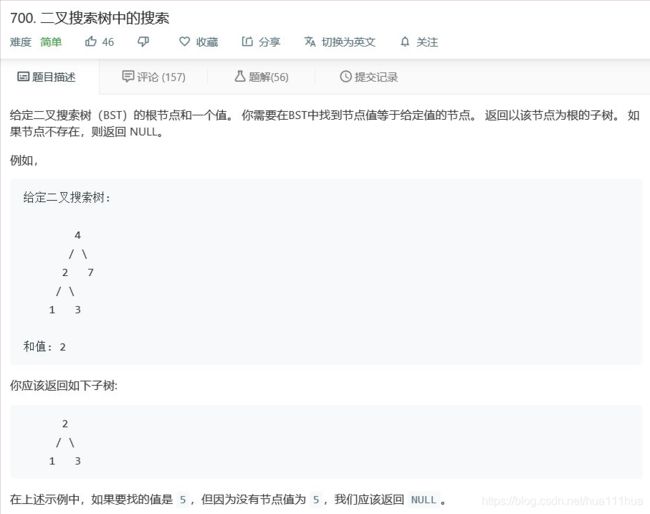
return result5.18 二叉搜索树中的搜索
def searchBST(self, root: TreeNode, val: int) :
if not root:
return None
if root.val==val:
return root
if root.val>val:
return self.searchBST(root.left,val)
else:
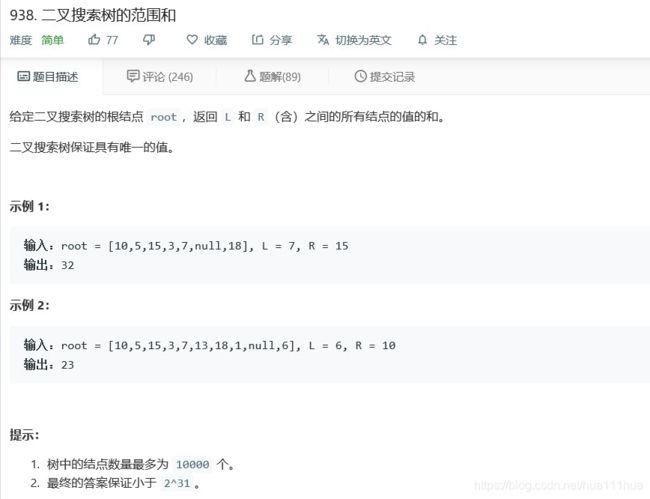
return self.searchBST(root.right,val)5.19 二叉搜索树的范围和
def rangeSumBST(self, root: TreeNode, L: int, R: int) -> int:
self.sum=0
def range(self,root,L,R):
if not root:
return None
self.range(root.left,L,R)
if root.val<=R and root.val>=L:
self.sum+=root.val
self.range(root.right,L,R)
range(root,L,R)
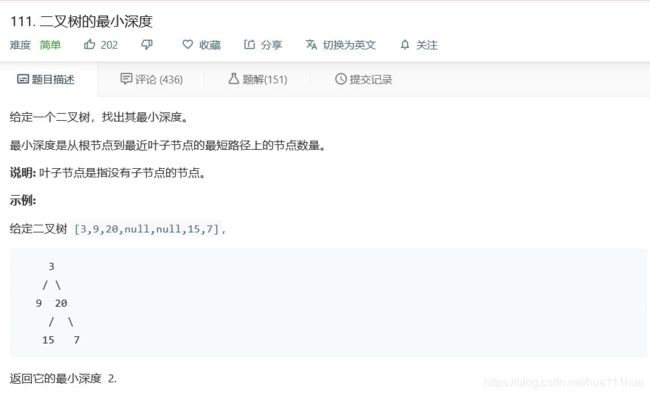
return self.sum5.19 二叉树的最小深度
def minDepth(self, root: TreeNode):
if not root:
return 0
if root.left is None or root.right is None:
return 1+max(self.minDepth(root.left),self.minDepth(root.right))
else:
return 1+min(self.minDepth(root.left),self.minDepth(root.right))5.20 N叉树的最大深度
def maxDepth(self, root: 'Node'):
if not root:
return 0
if not root.children:
return 1
return max(self.maxDepth(child)+1 for child in root.children)5.21 输出二叉树
def printTree(self, root: TreeNode):
h=0
def f(r,i):
if not r:
return
nonlocal h
h=max(h,i)
f(r.left,i+1)
f(r.right,i+1)
f(root,0)
n=2**(h+1)-1
a=[['']*n for _ in range(h+1)]
def g(r,i,j):
if not r:
return
a[i][j]=str(r.val)
s=(2**(h-i)-1)//2+1
g(r.left,i+1,j-s)
g(r.right,i+1,j+s)
g(root,0,n//2)
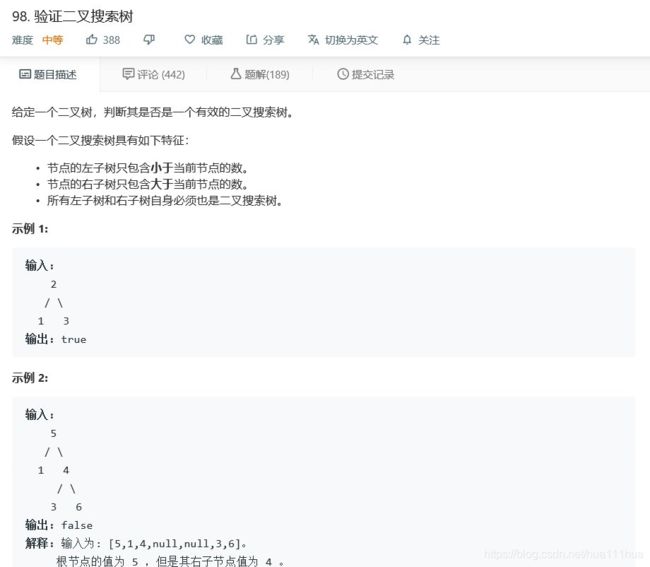
return a5.22 验证二叉搜索树
def isValidBST(self, root: TreeNode) :
inorder=self.inorder(root)
return inorder==list(sorted(set(inorder)))
def inorder(self,root):
if not root:
return []
return self.inorder(root.left)+[root.val]+self.inorder(root.right)5.23 恢复二叉搜索树
def recoverTree(self, root: TreeNode):
point=[]
val=[]
def inorder(root):
if not root:
return
inorder(root.left)
point.append(root)
val.append(root.val)
inorder(root.right)
return
inorder(root)
val=sorted(val)
for i in range(len(point)):
point[i].val=val[i]5.24 二叉树的所有路径
def binaryTreePaths(self, root: TreeNode):
if not root:
return []
if not root.left and not root.right:
return [str(root.val)]
paths=[]
if root.left:
for i in self.binaryTreePaths(root.left):
paths.append(str(root.val)+'->'+i)
if root.right:
for i in self.binaryTreePaths(root.right):
paths.append(str(root.val)+'->'+i)
return paths5.25 二叉树的最近公共祖先
def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') :
if not root or root==p or root==q:
return root
left=self.lowestCommonAncestor(root.left,p,q)
right=self.lowestCommonAncestor(root.right,p,q)
if not left and not right:
return None
elif left and right:
return root
else:
if not left:
return right
else:
return left5.26 二叉搜索树的最近公共祖先
def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode'):
if p.val<root.val and q.val<root.val:
return self.lowestCommonAncestor(root.left,p,q)
if p.val>root.val and q.val>root.val:
return self.lowestCommonAncestor(root.right,p,q)
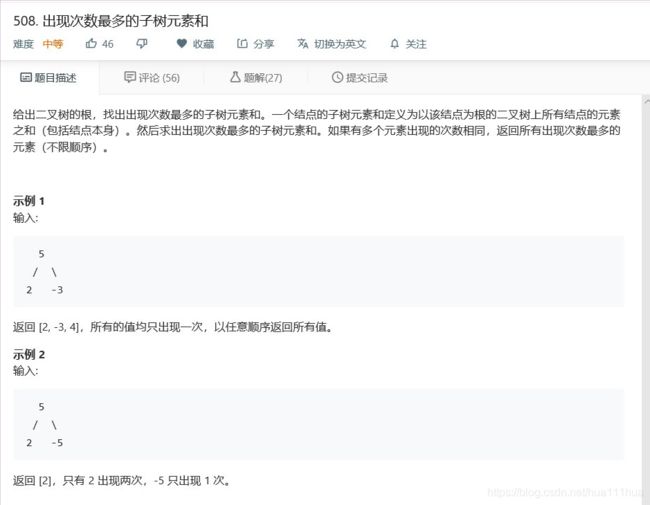
return root5.27出现次数最多的子树元素和
def findFrequentTreeSum(self, root: TreeNode) -> List[int]:
d={
}
def fun(node):
if not node:return
if node.left:
fun(node.left)
node.val+=node.left.val
if node.right:
fun(node.right)
node.val+=node.right.val
d[node.val]=d.get(node.val,0)+1
fun(root)
if not d:return []
m=max(d.values())
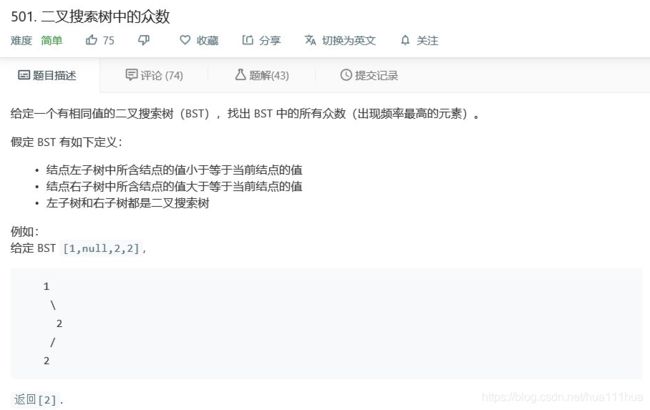
return [k for k,v in d.items() if v==m]5.28 二叉搜索树中的众数
def findFrequentTreeSum(self, root: TreeNode) :
d={
}
def fun(node):
if not node:return
if node.left:
fun(node.left)
node.val+=node.left.val
if node.right:
fun(node.right)
node.val+=node.right.val
d[node.val]=d.get(node.val,0)+1
fun(root)
if not d:return []
m=max(d.values())
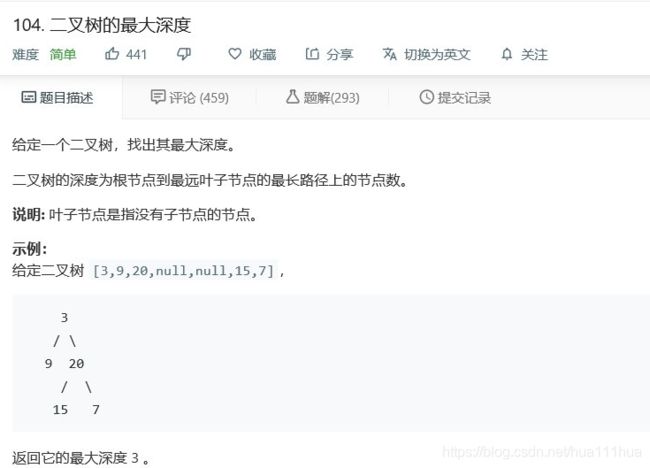
return [k for k,v in d.items() if v==m]5.29 二叉树的最大深度
def maxDepth(self, root: TreeNode) :
if not root :
return 0
else:
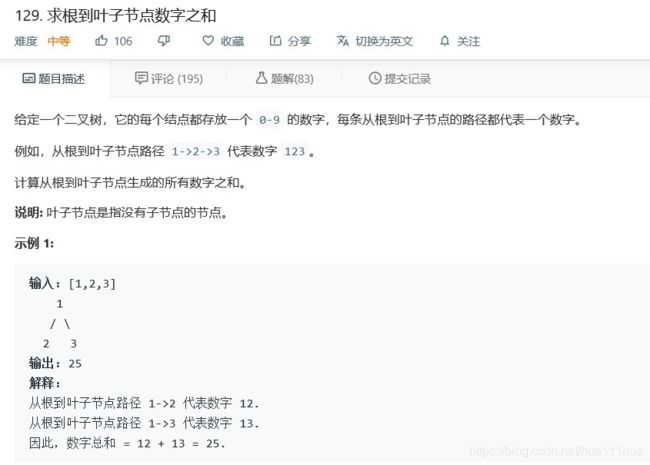
return 1+max(self.maxDepth(root.left),self.maxDepth(root.right))5.30 求根到叶子节点数字之和
def sumNumbers(self, root: TreeNode) :
def helper(root,sum):
if not root:
return 0
sum=sum*10
sum+=root.val
if root.left is None and root.right is None:
return sum
else:
return helper(root.left,sum)+helper(root.right,sum)
return helper(root,0)6.关于特殊要求的树
在树的题目中,会有一些特殊要求或者特殊结构的树,也需要注意下。
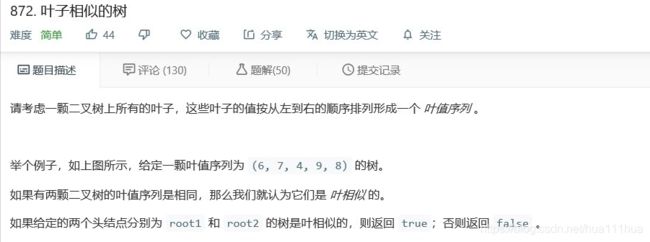
6.1 叶子相似的树
def leafSimilar(self, root1: TreeNode, root2: TreeNode):
def getleaf(self,root,res):
if not root:
return res
if not root.left and not root.right:
res.append(root.val)
if root.left:
self.getleaf(root.left,res)
if root.right:
self.getleaf(root.right,res)
return res
leaves1=getleaf(root1,[])
leaves2=getleaf(root2,[])
if str(leaves1)==str(leaves2):
return True
else:
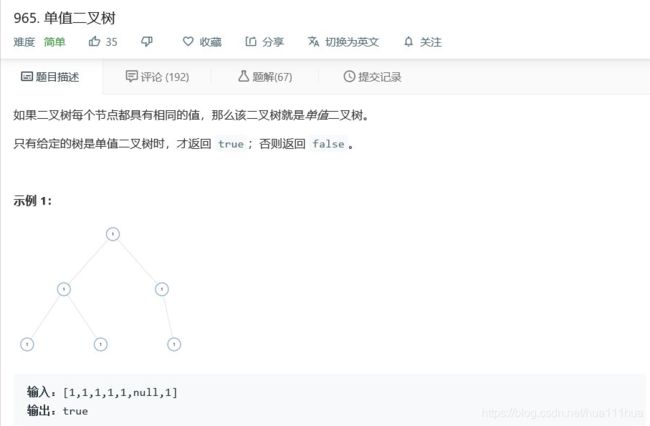
return False6.2 单值二叉树
def isUnivalTree(self, root: TreeNode):
res=[]
def inorder(self,root):
if not root:
return True
inorder(root.left)
res.append(root.val)
inorder(root.right)
inorder(root)
return True if len(set(res))==1 else False 6.3 最大二叉树
def constructMaximumBinaryTree(self, nums: List[int]):
if not nums:
return
max_num=max(nums)
max_num_index=nums.index(max_num)
root=TreeNode(max_num)
root.left=self.constructMaximumBinaryTree(nums[:max_num_index])
root.right=self.constructMaximumBinaryTree(nums[max_num_index+1:])
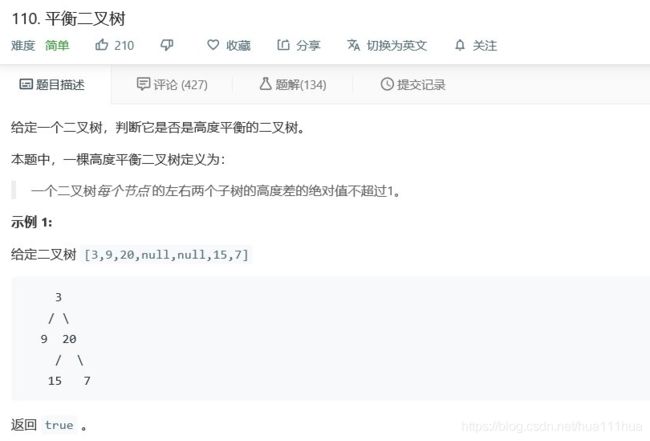
return root6.4 平衡二叉树
def isBalanced(self, root: TreeNode) :
if not root:
return True
if abs(self.depth(root.left)-self.depth(root.right))>1:
return False
return self.isBalanced(root.left) and self.isBalanced(root.right)
def depth(self,root):
if not root:
return 0
return max(self.depth(root.left),self.depth(root.right))+16.5 对称二叉树
def isSymmetric(self, root: TreeNode):
if not root:
return True
else:
return self.childTreeIsSymmetric(root.left,root.right)
def childTreeIsSymmetric(self,p,q):
if not p or not q:
return p==q
if p.val!=q.val:
return False
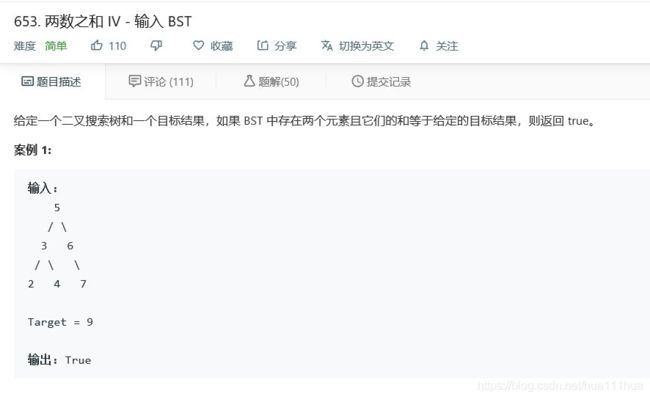
return self.childTreeIsSymmetric(p.left,q.right) and self.childTreeIsSymmetric(p.right,q.left)6.6 两数之和IV
def findTarget(self, root: TreeNode, k: int):
if not root:
return False
# 深度优先搜索
def dfs(node):
# target目标值与当前值求差
if k - node.val in exist:
self.res = True
return
else:
exist.add(node.val)
# 当前没有符合调条件的数据,继续
if not self.res:
if node.left:
dfs(node.left)
if node.right:
dfs(node.right)
exist = set()
self.res = False
dfs(root)
return self.res6.7 相同的树
def isSameTree(self, p: TreeNode, q: TreeNode) :
if not p and not q:
return True
elif p is not None and q is not None:
if p.val==q.val:
return self.isSameTree(p.left,q.left) and self.isSameTree(p.right,q.right)
else:
return False
else:
return False6.8 另一个树的子树
def isSubtree(self, s: TreeNode, t: TreeNode):
if not s:
return False
return self.isSame(s,t) or self.isSubtree(s.left,t) or self.isSubtree(s.right,t)
def isSame(self,s,t):
if s and t:
return s.val==t.val and self.isSame(s.left,t.left) and self.isSame(s.right,t.right)
elif s==t:
return True
else:
return False6.9 不同的二叉搜索树
def numTrees(self, n: int) :
dp = [0] * (n+1)
dp[0] = 1
dp[1] = 1
for i in range(2,n+1):
for j in range(1,i+1):
dp[i] += dp[j-1] * dp[i-j]
return dp[n]6.10 不同的二叉搜索树II
def generateTrees(self, n: int):
def generate_trees(start, end):
if start > end:
return [None,]
all_trees = []
for i in range(start, end + 1): # pick up a root
# all possible left subtrees if i is choosen to be a root
left_trees = generate_trees(start, i - 1)
# all possible right subtrees if i is choosen to be a root
right_trees = generate_trees(i + 1, end)
# connect left and right subtrees to the root i
for l in left_trees:
for r in right_trees:
current_tree = TreeNode(i)
current_tree.left = l
current_tree.right = r
all_trees.append(current_tree)
return all_trees
return generate_trees(1, n) if n else []6.11 对称二叉树
def isSymmetric(self, root: TreeNode):
if not root:
return True
else:
return self.childTreeIsSymmetric(root.left,root.right)
def childTreeIsSymmetric(self,p,q):
if not p or not q:
return p==q
if p.val!=q.val:
return False
return self.childTreeIsSymmetric(p.left,q.right) and self.childTreeIsSymmetric(p.right,q.left)7.关于树的应用
7.1 打家劫舍III
def rob(self, root: TreeNode):
def helper(root):
if not root:
return [0,0]
left=helper(root.left)
right=helper(root.right)
rob=root.val+left[1]+right[1]
skip=max(left)+max(right)
return [rob,skip]
res=helper(root)
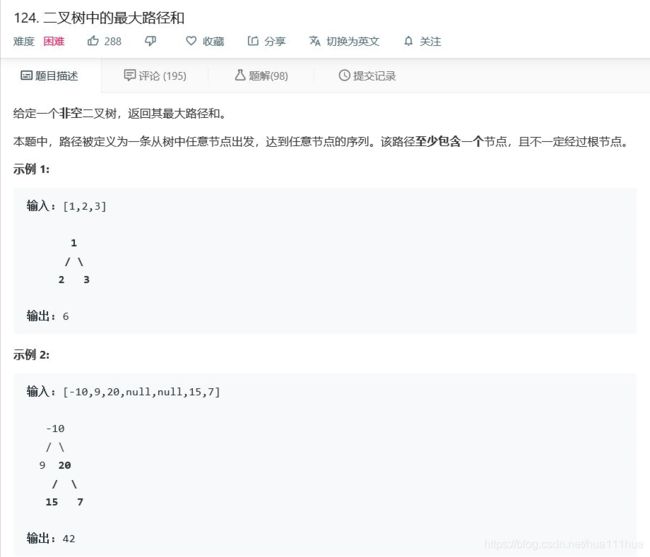
return max(res)7.2 二叉树中的最大路径和
def maxPathSum(self, root: TreeNode) :
self.max = float('-inf')
self.max_path(root)
return self.max
def max_path(self, root):
if not root: return 0
left = self.max_path(root.left)
right = self.max_path(root.right)
self.max = max(left + right + root.val, self.max)
tmp = max(left, right) + root.val
return tmp if tmp > 0 else 07.3 路径总和
def hasPathSum(self, root: TreeNode, sum: int) :
if not root :
return False
if not root.left and not root.right and root.val==sum:
return True
return self.hasPathSum(root.left,sum-root.val) or self.hasPathSum(root.right,sum-root.val)7.4 路径总和II
def pathSum(self, root: TreeNode, sum: int) :
res=[]
if not root:
return []
def helper(root,sum,tmp):
if not root:
return
if not root.left and not root.right and root.val==sum:
tmp+=[root.val]
res.append(tmp)
return
helper(root.left,sum-root.val,tmp+[root.val])
helper(root.right,sum-root.val,tmp+[root.val])
helper(root,sum,[])
return res7.5 路径总和III
class Solution:
def pathSum(self, root: TreeNode, sum: int) :
if not root:
return 0
return self.pathSum(root.left,sum)+self.pathSum(root.right,sum)+self.dfs(root,sum)
def dfs(self,node,sum):
if not node:
return 0
count=0
if node.val==sum:
count=1
return count+self.dfs(node.left,sum-node.val)+self.dfs(node.right,sum-node.val)