深度之眼Paper带读笔记NLP.23：Dialogue

前言

Adversarial Learning for Neural Dialogue Generation
对话生成的对抗学习
作者：Jiwei Li
单位：Stanford University
发表会议及时间：EMNLP2017
在线LaTeX公式编辑器
别人的翻译
代码复现
看到现在最懵逼的一篇文章。。。没有之一。。。
序列概率
常规的序列生成任务都是通过最大化序列生成概率，并通过MLE损失优化模型。
GAN
GAN是生成任务中火热的一类方法，通过对抗训练判别器与生成器，达到两方的那什均衡。
SeqGAN
GAN在设计之初是面向图像生成任务的，并不能直接应用于离散的NLP任务中，SeqGAN通过引入策略梯度和强化学习，为每个时间步的决策带来对应的奖赏，实现了GAN在生成任务中的应用。

第一课 论文导读

对话生成简介

对话生成

一般对话模型是用下面模型实现

Seq2Seq

传统的seq2seq模型倾向于生成安全，普适的回答，例如“I don’t know what you are talking about"。
传统的seq2seq模型的目标函数都是MLE函数，用MLE作为目标函数容易引起对话的死循环
需要能够生成多样化的、类人的回复

GAN

生成对抗网络（Generative Adversarial Networks，GAN）是通过对抗训练的方式来使得生成网络产生的样本服从真实数据分布。在生成对抗网络中，有两个网络进行对抗训练。一个是判别网络，目标是尽量准确地判断一个样本是来自于真实数据还是生成网络产生的；另一个是生成网络，目标是尽量生成判别网络无法区分来源的样本。这两个目标相反的网络不断地进行交替训练。当最后收敛时，如果判别网络再也无法判断出一个样本的来源，那么也就等价于生成网络可以生成符合真实数据分布的样本。
GAN的思想是是一种二人零和博弈思想（two-player game），博弈双方的利益之和是一个常数，比如两个人掰手腕，假设总的空间是一定的，你的力气大一点，那你就得到的空间多一点，相应的我的空间就少一点，相反我力气大我就得到的多一点，但有一点是确定的就是，我两的总空间是一定的，这就是二人博弈，但是呢总利益是一定的。
零和博弈（zero-sum game），又称零和游戏，与非零和博弈相对，是博弈论的一个概念，属非合作博弈。它是指参与博弈的各方，在严格竞争下，一方的收益必然意味着另一方的损失，博弈各方的收益和损失相加总和永远为“零”，双方不存在合作的可能。
### GAN中的生成网络和判别网络
生成网络从潜在空间（latent space）中随机采样作为输入，其输出结果需要尽量模仿训练集中的真实样本。生成网络是造样本的，它的目的就是使得自己造样本的能力尽可能强，强到什么程度呢，你判别网络没法判断我是真样本还是假样本。

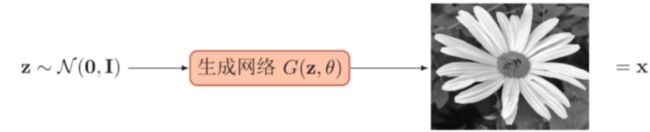
判别网络的输入则为真实样本或生成网络的输出，其目的是将生成网络的输出从真实样本中尽可能分辨出来。判别网络的目的就是能判别出来属于的一张图它是来自真实样本集还是假样本集。假如输入的是真样本，网络输出就接近1，输入的是假样本，网络输出接近0，那么很完美，达到了很好判别的目的。

对抗训练：生成网络要尽可能地欺骗判别网络。判别网络将生成网络生成的样本与真实样本中尽可能区分出来。两个网络相互对抗、不断调整参数，最终目的是使判别网络无法判断生成网络的输出结果是否真实。
判别网络说，我很强，来一个样本我就知道它是来自真样本集还是假样本集。生成网络就不服了，说我也很强，我生成一个假样本，虽然我生成网络知道是假的，但是你判别网络不知道呀，我包装的非常逼真，以至于判别网络无法判断真假，那么用输出数值来解释就是，生成网络生成的假样本进去了判别网络以后，判别网络给出的结果是一个接近0.5的值，极限情况就是0.5，也就是说判别不出来了，这就是纳什平衡（Nash equilibrium）了。

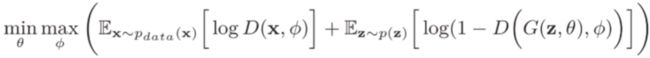
训练过程

优化D：
$$\underset{D}{\max }V(D,G)=E_{x\sim p_{data}(x)}[log(D(x))]+E_{z\sim p_z(z)}[log(1-(G(z)))]$$
优化G：
$$\underset{G}{\max }V(D,G)=E_{z\sim p_z(z)}[log(1-(G(z)))]$$

SeqGAN

序列概率

给定一个序列样本，其概率为$p(x_{1:T})=p(x_1,X_2,\dots ,x_T)=={\prod }_{t}p(x_t|x_{t-1},\dots ,x_1）$
生成问题：从已知的序列分布中生成新的序列样本
给定N个序列数据${\left\{x_{1:T_n}\right\}}_{n=1}^N$，序列概率模型需要学习一个模型来最大化整个数据集的对数似然函数:
$$\underset{\theta }{\max }\sum _{n=1}^{N}log{p}_{\theta }(x_{1:T_n})=\underset{\theta }{\max }\sum _{n=1}^N\sum _{t=1}^{T_n}log{p}_{\theta }(x_t|x_{1:t-1})$$
在这种序列模型方式中，每一步都需要将前面的输出作为当前步的输入，是一种自回归（autoregressive）的方式。

动机

序列生成模型一般是采用和任务相关的指标来进行评价，比如BLEU、ROUGE等，而训练时是使用最大似然估计，这导致训练目标和评价方法不一致。并且这些评价指标一般都是不可微的，无法直接使用基于梯度的方法来进行优化。

BLEU的设计思想与评判机器翻译好坏的思想是一致的：机器翻译结果越接近专业人工翻译的结果，则越好。BLEU算法实际上在做的事：判断两个句子的相似程度。

我想知道一个句子翻译前后的表示是否意思一致，显然没法直接比较，那我就拿这个句子的标准人工翻译与我的机器翻译的结果作比较，如果它们是很相似的，说明我的翻译很成功。因此，BLUE去做判断：一句机器翻译的话与其相对应的几个参考翻译作比较，算出一个综合分数。这个分数越高说明机器翻译得越好。
$$P_n=\frac{{\sum }_{n-gram\in y}coun{t}_{clip}(n-gram)}{{\sum }_{n-gram\in y}count(n-gram)}$$

能否使用GAN直接优化评价目标？
GAN应用于Sequence面临着两个问题：
问题1，GAN的设计初衷是用来能够生成连续的真实数据，但文本序列是非连续的。因为在GAN中，Generator是通过随机抽样作为开始，然后根据模型的参数进行确定性的转化。通过generative modelG的输出，discriminative model D算得损失值，根据得到的损失梯度去指导generative modelG做轻微改变，从而使G产生更加真实的数据。如果生成的数据是非连续的序列，那么这种来自D的“slight change"指导将变得几乎没有意义。因为在有限的Dictionary中，这种slight change没有相应的token。
问题2，GAN只能评估出整个生成序列的score/loss，不能够细化到去评估当前生成token的好坏和对后面生成的影响。

模型

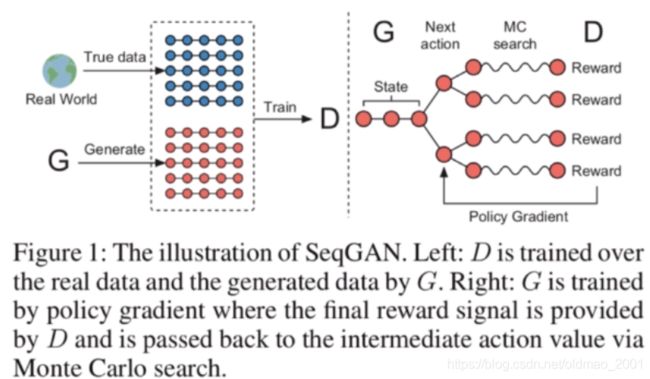
将序列产生问题看做是序列决策问题。生成器被认为是RL当中的agent；状态是目前已经产生的tokens，动作是下一步需要产生的 token。为了给出奖励，用discriminator 来评价 sequence，并且反馈评价来引导generative model的学习。
为了解决当输出是离散的，梯度无法回传给generative model的情况，将generative model看做是stochastic parameterized policy。采用MC搜索来近似 the state-action value。直接用policy gradient 来训练 policy，很自然的就避免了传统GAN中，离散数据的微分困难问题。

$$J(\theta )=E[R_T|s_0,\theta ]=\sum _{y_1\in Y}{G}_{\theta }(y_1|s_0)\cdot Q_{D_{\varphi }}^{G_{\theta }}(s_0,y_1)$$
序列生成任务可以描述如下：训练一个参数为$\theta$的生成模型$G_{\theta }$，用来生成序列$y_{1:T}=y_1,\dots ,y_t,\dots ,y_T,y_t\in Y$，Y表示候选词的词典。在第t时刻，state是当前生成的$tokens{y}_1,\dots ,y_{t-1}$，action是下一个$toke{n}_{yt}$的选择，policy是基于$G_{\theta }(y_t|y_{1:t-1})$做出的随机选择。Reward是鉴别器对生成句子的评估得分。如果判别器D认为给定的fake sequence是真的，其概率记为reward，此时：概率越高，reward 越大
$$Q_{D_{\varphi }}^{G_{\theta }}(a=y_T,s=Y_{1:T-1})=D_{\varphi }(Y_{1:T})$$
然而，这个discriminator仅仅提供了一个reward 给一个已经结束的sequence。我们需要计算每个动作也就是每个时刻词项的选择对最终结果的影响，也就是评估中间态的动作值函数。为了实现这一目的，当解码到t时，即对后面T-t个timestep采用蒙特卡洛搜索和roll-out策略搜索出N条路径，将这N条路径分别和已经decode的结果组成N条完整输出，然后将D网络对应奖励的平均值作为reward。蒙特卡洛搜索是指在选择下一个节点的时候用蒙特卡洛采样的方式，而蒙特卡洛采样是指根据当前输出词表的置信度随机采样。

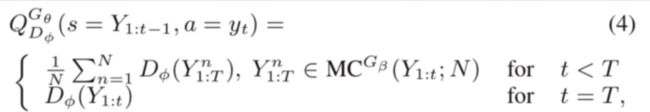
蒙特卡洛搜索如下图：

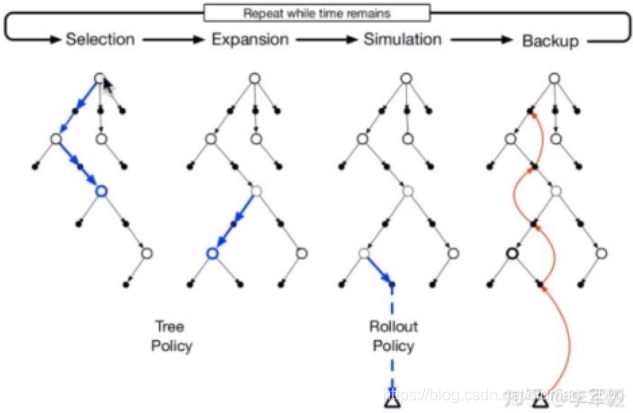
roll-out 算法是对于当前状态，从每一个可能的动作开始，之后根据给定的策略进行路径采样，根据多次采样的奖励总和来对当前状态的行动值进行估计。当当前估计基本收敛时，会根据行动值最大的原则选择动作进入下一个状态再重复上述过程。在蒙特卡洛控制中，采样的目的是估计一个完整的，最优价值函数，但是roll-out中的采样目的只是为了计算当前状态的行动值以便进入下一个状态，而且这些估计的行动值并不会被保留。在roll-out中采用的策略往往比较简单被称作 roll-out 策略（roll-out policy）。

前期知识储备

对话生成：了解对话生成的基本任务
GAN：掌握GAN的思想
SeqGAN：掌握SeqGAN的关键技术，包括蒙特卡洛采样、对抗训练策略

参考文献

Deep reinforcement learning for dialogue generation

第二课 论文精读

内容和第一节一致。。。

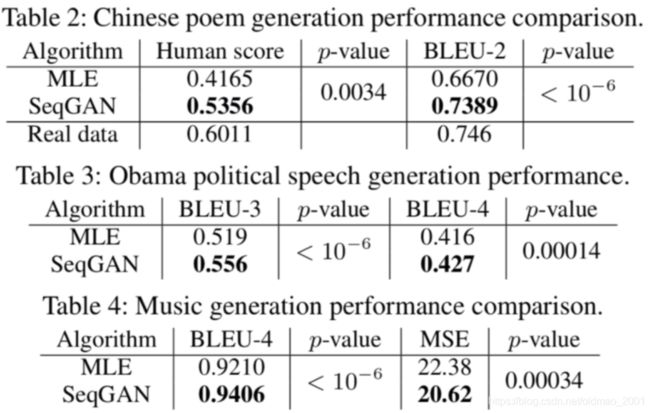
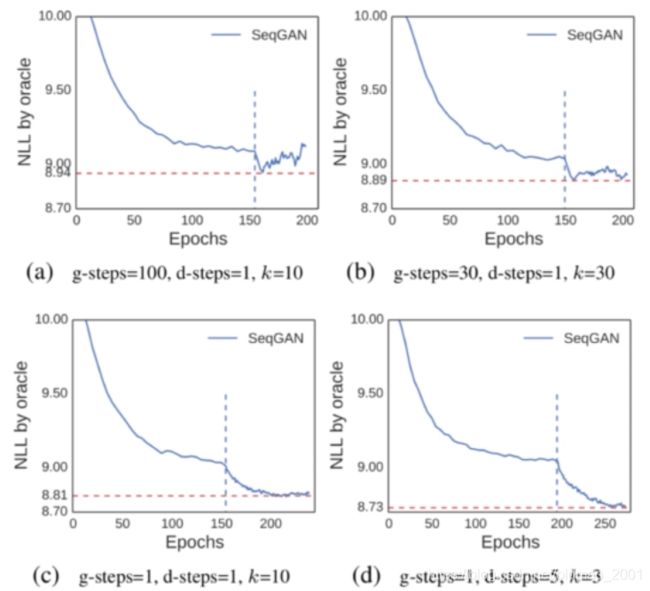
实验结果

序列生成

讨论

总结

A 将GAN应用到了文本生成中
1.蒙特卡洛采样生成reward
2.预训练及对抗训练策略
B.证明了GAN也可以应用于文本生成，并能取得比MLE更好的效果
C.对后续工作有很大启发，如QA，实验分析十分详尽

作业

阅读后续改进工作：RankGAN（NIPS 2017）以及MaskGAN（ICLR 2018）