卷积的物理意义

  在学信号与系统时就知道有卷积这么个东西了，但当时只知道卷积公式以及卷积含义，自己尝试过从物理意义角度取理解它，不是很明白，这次使用mathematica仿真一下。

---

卷积

我们知道，系统的响应等于激励信号与冲激响应的卷积，对于因果信号：

$$y(t)={\int }_0^{\infty }f(\tau )h(t-\tau )d\tau$$

这个式子可以直接拿来用，比如：

h = E^(-2 t) UnitStep[t];
f = E^-t*(t + 1);
y = Convolve[h, f, t, z];
Plot[y, {z, 0, 5}, PlotRange -> All]

---

理解

卷积积分可以这样来理解：
如果我们再一次冲激响应之后对系统再来一个冲激函数激励，将会得到两次冲激响应的叠加，如图：

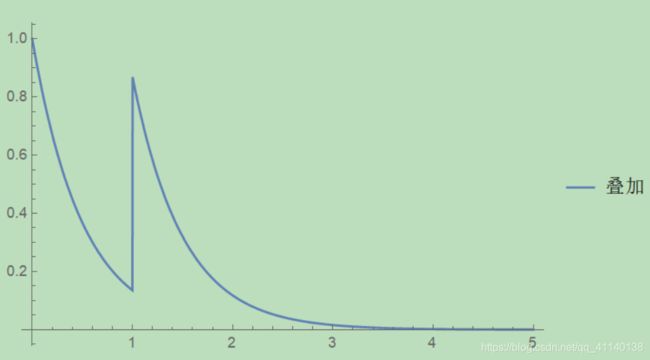
  注意，不同的冲激响应的幅度可以不同，我们取每一次冲激响应的强度等于原先激励信号f(t)在该此刻的幅度。

  上一个图，两次冲激响应的间隔为1s，如果将时间间隔减小为0.1s, 0.05s呢？

  可以看出，在上一个激励衰减，下一个激励补偿的过程中，不同的冲激响应的叠加的结果与激励信号单独作用的结果。

---

从叠加到卷积公式

我们对比取不同时间间隔，将响应叠加后的效果绘制出来：

F[t_] := E^-t*(t + 1)
H[t_] := E^(-2 t) UnitStep[t]
dt = 0.1;
amount = 1/dt;
Y1 = 1/(1/dt) Sum[H[t - k*dt]*F[k*dt], {k, 0, 5*amount}];
dt = 0.01;
amount = 1/dt;
Y2 = 1/(1/dt) Sum[H[t - k*dt]*F[k*dt], {k, 0, 5*amount}];
Plot[{Y1, Y2, y /. z -> t}, {t, 0, 5}, PlotRange -> All , 
 Exclusions -> None, PlotLegends -> {"dt=0.1", "dt=0.01", "convolve"}]

结果如图：

  可以推测，当时间间隔dt趋于0时，无数个冲激响应的和就是激励f(t)单独作用时习题的响应，此时累加变为积分，就得到卷积公式了，我们也可以理解为：取无限小的时间间隔，在每一个时间间隔中的f(t)看作一个小的冲激函数，每一个成绩函数对应一个冲激响应，那么总的响应就是成绩响应的叠加，dt无限小就成了积分。