贝叶斯分类(模式识别_Matlab实现:附具体实现代码)
最近学习了《计算机模式识别》中的贝叶斯分类原理,老师也讲到这种方法的实现过程及Matlab代码实现过程(代码由老师提供),在此感谢我的赵宗泽赵老师。下面我将个人的理解写了篇小文章,希望对需要的朋友有所帮助,理解有误或不足之处还望大家及时指出纠正。
整个分类流程:
进行贝叶斯分类首先要进行最大似然估计,得出最大似然估计量然后进行贝叶斯分类。
1.进行最大似然估计首先要生成训练样本:
下面是生成训练样本的matlab代码:
randn('seed', 0);
[X_train, Y_train] = generate_gauss_classes(Mu, S, P, N);
figure();
hold on;
class1_data = X_train(:, Y_train==1);
class2_data = X_train(:, Y_train==2);
plot(class1_data(1, :), class1_data(2, :), 'r.');
plot(class2_data(1, :), class2_data(2, :), 'g.');
grid on;
title('Train');
xlabel('N=500');
同时生成测试样本:
randn('seed', 100);
[X_test, Y_test] = generate_gauss_classes(Mu, S, P, N);
figure();
hold on;
test1_data = X_test(:, Y_test==1);
test2_data = X_test(:, Y_test==2);
plot(test1_data(1, :), test1_data(2, :), 'r.');
plot(test2_data(1, :), test2_data(2, :), 'g.');
grid on;
title('Test');
xlabel('N=500');
2.下面利用最大似然估计来计算最大似然估计量:
% 各类样本只包含本类分布的信息,也就是说不同类别的参数在函数上是独立的
[mu1_hat, s1_hat] = gaussian_ML_estimate(class1_data);
[mu2_hat, s2_hat] = gaussian_ML_estimate(class2_data);
mu_hat = [mu1_hat, mu2_hat];
s_hat = (1/2) * (s1_hat + s2_hat);
得到最大似然估计量之后就可以进行贝叶斯分类啦,首先给大家讲一下什么是贝叶斯分类及分类的流程:
贝叶斯分类流程:
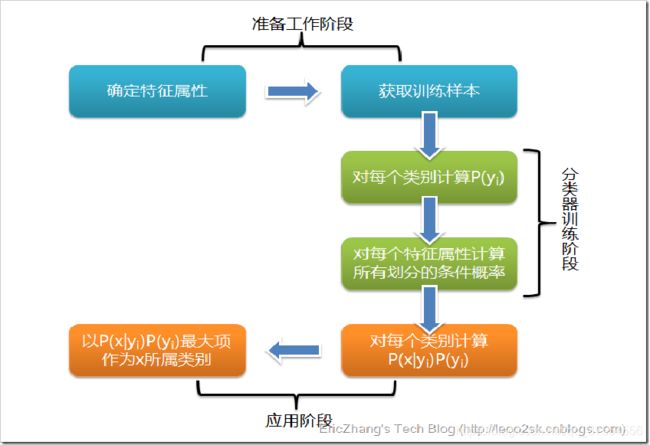
下面是贝叶斯分类的三个过程详述:
第一阶段——准备工作阶段,这个阶段的任务是为朴素贝叶斯分类做必要的准备,主要工作是根据具体情况确定特征属性,并对每个特征属性进行适当划分,然后由人工对一部分待分类项进行分类,形成训练样本集合。这一阶段的输入是所有待分类数据,输出是特征属性和训练样本。这一阶段是整个朴素贝叶斯分类中唯一需要人工完成的阶段,其质量对整个过程将有重要影响,分类器的质量很大程度上由特征属性、特征属性划分及训练样本质量决定。
第二阶段——分类器训练阶段,这个阶段的任务就是生成分类器,主要工作是计算每个类别在训练样本中的出现频率及每个特征属性划分对每个类别的条件概率估计,并将结果记录。其输入是特征属性和训练样本,输出是分类器。这一阶段是机械性阶段,根据前面讨论的公式可以由程序自动计算完成。
第三阶段——应用阶段。这个阶段的任务是使用分类器对待分类项进行分类,其输入是分类器和待分类项,输出是待分类项与类别的映射关系。这一阶段也是机械性阶段,由程序完成。
3.下面用测试样本和估计出的参数进行分类:
% 使用欧式距离进行分类
z_euclidean = euclidean_classifier(mu_hat, X_test);
% 使用贝叶斯方法进行分类
z_bayesian = bayes_classifier(Mu, S, P, X_test);
4.接着计算不同方法分类的误差:
err_euclidean = ( 1-length(find(Y_test == z_euclidean')) / length(Y_test) );
err_bayesian = ( 1-length(find(Y_test == z_bayesian')) /length(Y_test) );
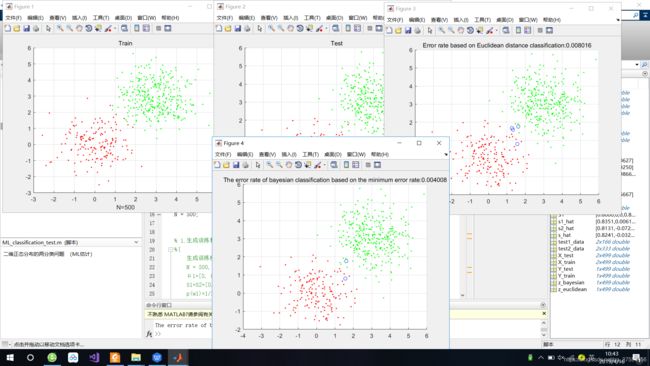
5.最后将分类的结果及误差展示出来:
% 二维正态分布的两分类问题 (ML估计)
clc;
clear;
% 两个类别数据的均值向量
Mu = [0 0; 3 3]';
% 协方差矩阵
S1 = 0.8 * eye(2);
S(:, :, 1) = S1;
S(:, :, 2) = S1;
% 先验概率(类别分布)
P = [1/3 2/3]';
% 样本数据规模
% 收敛性:无偏或者渐进无偏,当样本数目增加时,收敛性质会更好
N = 500;
% 1.生成训练和测试数据
%{
生成训练样本
N = 500, c = 2, d = 2
μ1=[0, 0]' μ2=[3, 3]'
S1=S2=[0.8, 0; 0.8, 0]
p(w1)=1/3 p(w2)=2/3
%}
randn('seed', 0);
[X_train, Y_train] = generate_gauss_classes(Mu, S, P, N);
figure();
hold on;
class1_data = X_train(:, Y_train==1);
class2_data = X_train(:, Y_train==2);
plot(class1_data(1, :), class1_data(2, :), 'r.');
plot(class2_data(1, :), class2_data(2, :), 'g.');
grid on;
title('Train');
xlabel('N=500');
%{
用同样的方法生成测试样本
N = 500, c = 2, d = 2
μ1=[0, 0]' μ2=[3, 3]'
S1=S2=[0.8, 0; 0.8, 0]
p(w1)=1/3 p(w2)=2/3
%}
randn('seed', 100);
[X_test, Y_test] = generate_gauss_classes(Mu, S, P, N);
figure();
hold on;
test1_data = X_test(:, Y_test==1);
test2_data = X_test(:, Y_test==2);
plot(test1_data(1, :), test1_data(2, :), 'r.');
plot(test2_data(1, :), test2_data(2, :), 'g.');
grid on;
title('Test');
xlabel('N=500');
% 2.用训练样本采用ML方法估计参数
% 各类样本只包含本类分布的信息,也就是说不同类别的参数在函数上是独立的
[mu1_hat, s1_hat] = gaussian_ML_estimate(class1_data);
[mu2_hat, s2_hat] = gaussian_ML_estimate(class2_data);
mu_hat = [mu1_hat, mu2_hat];
s_hat = (1/2) * (s1_hat + s2_hat);
% 3.用测试样本和估计出的参数进行分类
% 使用欧式距离进行分类
z_euclidean = euclidean_classifier(mu_hat, X_test);
% 使用贝叶斯方法进行分类
z_bayesian = bayes_classifier(Mu, S, P, X_test);
% 4.计算不同方法分类的误差
err_euclidean = ( 1-length(find(Y_test == z_euclidean')) / length(Y_test) );
err_bayesian = ( 1-length(find(Y_test == z_bayesian')) / length(Y_test) );
% 输出信息
disp(['Error rate based on Euclidean distance classification:', num2str(err_euclidean)]);
disp(['The error rate of bayesian classification based on the minimum error rate:', num2str(err_bayesian)]);
**贝叶斯分类:**
% 画图展示
figure();
hold on;
z_euclidean = transpose(z_euclidean);
o = 1;
q = 1;
for i = 1:size(X_test, 2)
if Y_test(i) ~= z_euclidean(i)
plot(X_test(1,i), X_test(2,i), 'bo');
elseif z_euclidean(i)==1
euclidean_classifier_results1(:, o) = X_test(:, i);
o = o+1;
elseif z_euclidean(i)==2
euclidean_classifier_results2(:, q) = X_test(:, i);
q = q+1;
end
end
plot(euclidean_classifier_results1(1, :), euclidean_classifier_results1(2, :), 'r.');
plot(euclidean_classifier_results2(1, :), euclidean_classifier_results2(2, :), 'g.');
title(['Error rate based on Euclidean distance classification:', num2str(err_euclidean)]);
grid on;
figure();
hold on;
z_bayesian = transpose(z_bayesian);
o = 1;
q = 1;
for i = 1:size(X_test, 2)
if Y_test(i) ~= z_bayesian(i)
plot(X_test(1,i), X_test(2,i), 'bo');
elseif z_bayesian(i)==1
bayesian_classifier_results1(:, o) = X_test(:, i);
o = o+1;
elseif z_bayesian(i)==2
bayesian_classifier_results2(:, q) = X_test(:, i);
q = q+1;
end
end
plot(bayesian_classifier_results1(1, :), bayesian_classifier_results1(2, :), 'r.');
plot(bayesian_classifier_results2(1, :), bayesian_classifier_results2(2, :), 'g.');
title(['The error rate of bayesian classification based on the minimum error rate:', num2str(err_bayesian)]);
grid on;
function [ z ] = bayes_classifier( m, S, P, X )
%{
函数功能:
利用基于最小错误率的贝叶斯对测试数据进行分类
参数说明:
m:数据的均值
S:数据的协方差
P:数据类别分布概率
X:我们需要测试的数据
函数返回:
z:数据所属的分类
%}
[~, c] = size(m);
[~, n] = size(X);
z = zeros(n, 1);
t = zeros(c, 1);
for i = 1:n
for j = 1:c
t(j) = P(j) * comp_gauss_dens_val( m(:,j), S(:,:,j), X(:,i) );
end
[~, z(i)] = max(t);
end
end
计算高斯分布N(m, s),在某一个特定点的值
function [ z ] = comp_gauss_dens_val( m, s, x )
%{
参数说明:
m:数据的均值
s:数据的协方差
x:我们需要计算的数据点
函数返回:
z:高斯分布在x出的值
%}
z = ( 1/( (2*pi)^(1/2)*det(s)^0.5 ) ) * exp( -0.5*(x-m)'*inv(s)*(x-m) );
end
利用欧式距离对测试数据进行分类
function [ z ] = euclidean_classifier( m, X )
%{
参数说明:
m:数据的均值,由ML对训练数据,参数估计得到
X:我们需要测试的数据
函数返回:
z:数据所属的分类
%}
[~, c] = size(m);
[~, n] = size(X);
z = zeros(n, 1);
de = zeros(c, 1);
for i = 1:n
for j = 1:c
de(j) = sqrt( (X(:,i)-m(:,j))' * (X(:,i)-m(:,j)) );
end
[~, z(i)] = min(de);
end
end
最大似然估计:
样本正态分布的最大似然估计
function [ m_hat, s_hat ] = gaussian_ML_estimate( X )
%{
函数功能:
样本正态分布的最大似然估计
参数说明:
X:训练样本
函数返回:
m_hat:样本由极大似然估计得出的正态分布参数,均值
s_hat:样本由极大似然估计得出的正态分布参数,方差
%}
% 样本规模
[~, N] = size(X);
% 正态分布样本总体的未知均值μ的极大似然估计就是训练样本的算术平均
m_hat = (1/N) * sum(transpose(X))';
% 正态分布中的协方差阵Σ的最大似然估计量等于N个矩阵的算术平均值
s_hat = zeros(1);
for k = 1:N
s_hat = s_hat + (X(:, k)-m_hat) * (X(:, k)-m_hat)';
end
s_hat = (1/N)*s_hat;
end
生成样本数据:
function [ data, C ] = generate_gauss_classes( M, S, P, N )
%{
函数功能:
生成样本数据,符合正态分布
参数说明:
M:数据的均值向量
S:数据的协方差矩阵
P:各类样本的先验概率,即类别分布
N:样本规模
函数返回
data:样本数据(2*N维矩阵)
C:样本数据的类别信息
%}
[~, c] = size(M);
data = [];
C = [];
for j = 1:c
% z = mvnrnd(mu,sigma,n);
% 产生多维正态随机数,mu为期望向量,sigma为协方差矩阵,n为规模。
% fix 函数向零方向取整
t = mvnrnd(M(:,j), S(:,:,j), fix(P(j)*N))';
data = [data t];
C = [C ones(1, fix(P(j) * N)) * j];
end
end
代码操作说明:
运行之前需要把文件的路径添加到matlab,然后,运行ML_classification_test.m文件,其他文件都是函数。