《算法导论》第三版第12章 二叉搜索树 练习&思考题 个人答案

12.1 什么是二叉搜索树

12.1-1

高度为 2:
高度为3：

高度为4：

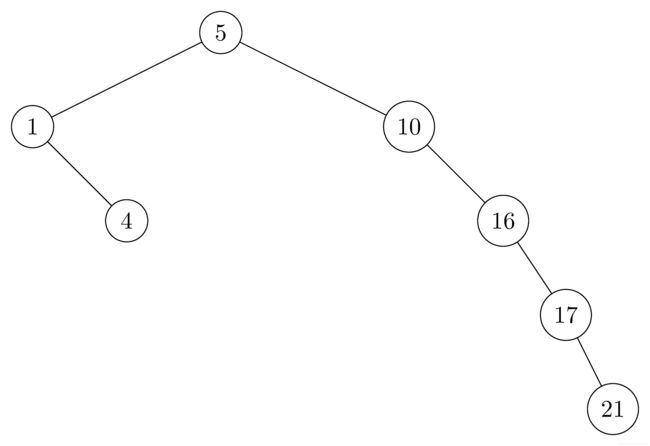
高度为5：

高度为6：

12.1-2

解：最小堆的结点值总不大于孩子结点的值，而二叉搜索树的结点值不小于左子树元素结点的值，不大于右子树元素结点的值；最小堆性质无法在O(n)时间内按序输出一棵有n个结点树的关键字，因为堆（以最小堆为例）无法告知大于当前结点的最小元素是在左子树还是在右子树。
换一个角度考虑，如果真的有这种方法，意味着存在O(n)时间的比较排序算法，而这被证明是不存在的。

12.1-3

解：

INORDER-TREE-WALK(T)
let S be an empty stack
current = T.root
done = 0
while !done
    if current != NIL
        PUSH(S, current)
        current = current.left
    else
        if !S.EMPTY()
            current = POP(S)
            print current
            current = current.right
        else done = 1

12.1-4

解：

PREORDER-TREE-WALK(x)
if x != NIL
    print x.key
    PREORDER-TREE-WALK(x.left)
    PREORDER-TREE-WALK(x.right)

POSTORDER-TREE-WALK(x)
if x != NIL
    POSTORDER-TREE-WALK(x.left)
    POSTORDER-TREE-WALK(x.right)
    print x.key

递归真的好用。

12.1-5

证明：反证法，假设我们可以使用小于$\Omega (n\lg n)$的时间，因为遍历二叉搜索树只需要$\Theta (n)$，我们就可以得到小于$\Omega (n\lg n)$的比较排序算法，这与第8章的证明相矛盾。（也就类似于12.1-3的思路了）

12.2 查询二叉搜索树

12.2-1

解：c（先找到911后找到912不可能）和e（先找到347后找到299不可能）。

12.2-2

解：

TREE-MINIMUM(x)
while x.left != NIL
    return TREE-MINIMUM(x.left)
return x

TREE-MAXIMUM(x)
while x.right != NIL
    return TREE-MAXIMUM(x.right)
return x

12.2-3

解：

TREE-PREDECESSOR(x)
if x.left != NIL
    return TREE-MAXIMUM(x.left)
y = x.p
while y != NIL and x == y.left
    x = y
    y = y.p
return y

12.2-4

思路：例如在查找过程中某一结点x的右孩子的两个孩子结点选择了右边，x的右孩子的左孩子就归到A集合，但该数还是比B集合中的x大。

12.2-5

证明：结点x的后继s一定位于x的右子树，而后继s如果有左孩子，该左孩子肯定还是位于x的右子树，那么该左孩子的值就介于x和s之间，那么s就不是x的后继了，矛盾；对称地可证明前驱没有右孩子。

12.2-6

证明：首先，我们确定$y$必须是$x$的祖先。如果$y$不是$x$的祖先，那么让$z$表示$x$和$y$的第一个共同祖先。根据二叉搜索树属性，$x<z<y$，因此$y$不能是$x$的后继。接下来注意$y.left$必须是$x$的祖先，因为如果不是，那么$y.right$将是$x$的祖先，暗示$x>y$。最后，假设$y$不是$x$的最底层祖先，其左孩子也是$x$的祖先。让$z$表示这个最底层祖先。那么$z$必须在$y$的左子树中，这意味着$z<y$，这与$y$是$x$的后继相矛盾。

12.2-7

证明（来自参考答案）：
Note that a call to $\text{TREE-MINIMUM}$ followed by $n-1$ calls to $\text{TREE-SUCCESSOR}$ performs exactly the same inorder walk of the tree as does the procedure $\text{INORDER-TREE-WALK}$. $\text{INORDER-TREE-WALK}$ prints the $\text{TREE-MINIMUM}$ first, and by
definition, the $\text{TREE-SUCCESSOR}$ of a node is the next node in the sorted order determined by an inorder tree walk.
This algorithm runs in $\Theta (n)$ time because:

It requires $O(n)$ time to do the n procedure calls.
It traverses each of the $n-1$ tree edges at most twice, which takes $O(n)$ time.

To see that each edge is traversed at most twice (once going down the tree and once going up), consider the edge between any node $u$ and either of its children, node $v$. By starting at the root, we must traverse $(u,v)$ downward from $u$ to $v$, before traversing it upward from $v$ to $u$. The only time the tree is traversed downward is in code of $\text{TREE-MINIMUM}$, and the only time the tree is traversed upward is in code of $\text{TREE-SUCCESSOR}$ when we look for the successor of a node that has no right subtree.
Suppose that is $u$'s left child.

Before printing $u$, we must print all the nodes in its left subtree, which is rooted at $v$, guaranteeing the downward traversal of edge $(u,v)$.
After all nodes in $u$'s left subtree are printed, $u$ must be printed next. Procedure $\text{TREE-SUCCESSOR}$ traverses an upward path to $u$ from the maximum element (which has no right subtree) in the subtree rooted at . This path clearly includes edge $(u,v)$, and since all nodes in $u$'s left subtree are printed, edge $(u,v)$ is never traversed again.

Now suppose that $v$ is $u$'s right child.

After $u$ is printed, $\text{TREE-SUCCESSOR}(u)$ is called. To get to the minimum element in $u$'s right subtree (whose root is $v$), the edge $(u,v)$ must be traversed downward.
After all values in $u$'s right subtree are printed, $\text{TREE-SUCCESSOR}$ is called on the maximum element (again, which has no right subtree) in the subtree rooted at $v$. $\text{TREE-SUCCESSOR}$ traverses a path up the tree to an element after $u$, since $u$ was already printed. Edge $(u,v)$ must be traversed upward on this path, and since all nodes in $u$'s right subtree have been printed, edge $(u,v)$ is never traversed again.

Hence, no edge is traversed twice in the same direction.
Therefore, this algorithm runs in $\Theta (n)$ time.

12.2-8

证明：假设$x$是起始节点，$y$是结束节点。$x$和$y$之间的距离最多为$2h$，连接$k$节点的所有边都被访问两次，因此需要$O(k+h)$时间。

12.2-9

证明：
假设$x$是$y$的左孩子，那么$y.key>x.key$，以及$y$可能有的右子树的关键字都大于$y.key$，且$x$是叶结点没有右孩子，所以$y.key$是$T$树中大于$x.key$的最小关键字；
假设$x$是$y$的右孩子，那么$y.key<x.key$，以及$y$可能有的左子树的关键字都小于$y.key$，且$x$是叶结点没有左孩子，所以$y.key$是$T$树中小于$x.key$的最大关键字。

12.3 插入和删除

12.3-1

解：

RECURSIVE-TREE-INSERT(T, z)
if T.root = NIL
    T.root = z
else INSERT(NIL, T.root, z)

INSERT(p, x, z)
if x == NIL
    z.p = p
    if z.key < p.key
        p.left = z
    else 
        p.right = z
else if z.key < x.key
    INSERT(x, x.left, z)
else 
    INSERT(x, x.right, z)

12.3-2

证明：易证路径是一样的，又因为搜索时检查的节点数也包括搜索到的节点，所以……

12.3-3

解：

TREE-SORT(A)
let T be an empty binary search tree
for i = 1 to A.length
    TREE-INSERT(A[i])
INORDER-TREE-WALK(T.root)

最坏情况：$\Theta (n^2)$ - 当重复的$\text{TREE-INSERT}$操作产生一个线性结点链时。
最好情况：$\Theta (n\lg n)$ - 当重复的$\text{TREE-INSERT}$操作产生高度为$\Theta (\lg n)$的二叉树时。

12.3-4

解：不一样

先删除A，再删除B：

  A        C        C
 / \      / \        \
B   D    B   D        D
   /
  C
先删除B，再删除A：
  A        A        D
 / \        \      /
B   D        D    C
   /        /
  C        C

12.3-5

解：

PARENT(z)
if z == NIL
    m = T.root
else 
    m = z.left
while m != x
    p = m
    m = m.right
return p

GET-PARENT(T, x)
if x.right == NIL
    if x == x.succ.left
        x.p = x.succ
    else
        z = x.succ
        x.p = PARENT(z)
else
    y = TREE-MAXIMUM(x.right)
    if x == y.succ.left
        x.p = y.succ
    else
        z = y.succ
        x.p = PARENT(z)

12.3-6

思路：可以在原函数第5行添加一个RANDOM(0,1)，返回0选择前驱，返回1选择后继即可。

12.4 随机构建二叉搜索树

12.4-1

证明：
$$\begin{array}{rl}\sum _{i=0}^{n-1}\left(\genfrac{}{}{0ex}{}{i+3}{3}\right)& =\sum _{i=0}^{n-1}\frac{(i+3)(i+2)(i+1)}{6}\\ & =\frac{1}{6}\sum _{i=0}^{n-1}{i}^3+6i^2+11i+6\\ & =\frac{1}{6}(\frac{(n-1{)}^2{n}^2}{4}+\frac{6(n-1)n(2n-1)}{6}+\frac{11n(n-1)}{2}+6n)\\ & =\frac{n(n+1)(n+2)(n+3)}{24}\\ & =\left(\genfrac{}{}{0ex}{}{n+3}{4}\right).\end{array}$$

12.4-2

证明（来自参考答案）：
We will answer the second part first. We shall show that if the average depth of a p node is $\Theta (\lg n)$, then the height of the tree is $O(n\lg n)$. Then we will answer the first part by exhibiting that this bound is tight: there is a binary search tree with p average node depth $\Theta (\lg n)$ and height $\Theta (\sqrt{n\lg n})=\omega (\lg n)$.
Lemma
If the average depth of p a node in an $n$-node binary search tree is $\Theta (\lg n)$, then the height of the tree is $O(\sqrt{n\lg n})$.
Proof
Suppose that an $n$-node binary search tree has average depth $\Theta (\lg n)$ and height $h$. Then there exists a path from the root to a node at depth $h$, and the depths of the nodes on this path are $0,1,\dots ,h$. Let $P$ be the set of nodes on this path and $Q$ be all other nodes. Then the average depth of a node is
$$\begin{array}{rl}\frac{1}{n}(\sum _{x\in P}\text{depth(x)}+\sum _{y\in Q}\text{depth(y)})& \ge \frac{1}{n}\sum _{x\in P}\text{depth(x)}\\ & =\frac{1}{n}\sum _{d=0}^{h}d\\ & =\frac{1}{n}\cdot \Theta (h^2).\end{array}$$
For the purpose of contradiction, suppose that $h$ is not $O(\sqrt{n\lg n})$, so that $h=\omega (\sqrt{n\lg n})$. Then we have
$$\begin{array}{rl}\frac{1}{n}\cdot \Theta (h^2)& =\frac{1}{n}\cdot \omega (n\lg n)\\ & =\omega (\lg n),\end{array}$$
which contradicts the assumption that the average depth is $\Theta (\lg n)$. Thus, the height is $O(\sqrt{n\lg n})$.
Here is an example of an $n$-node binary search tree with average node depth $\Theta (\lg n)$ but height $\omega (\lg n)$:

In this tree, $n-\sqrt{n\lg n}$ nodes are a complete binary tree, and the other $\sqrt{n\lg n}$ nodes protrude from below as a single chain. This tree has height
$$\begin{array}{rl}\Theta (\lg (n-\sqrt{n\lg n}))+\sqrt{n\lg n}& =\Theta (\sqrt{n\lg n})\\ & =\omega (\lg n).\end{array}$$
To compute an upper bound on the average depth of a node, we use $O(\lg n)$ as an upper bound on the depth p of each of the $n-\sqrt{n\lg n}$ nodes in the complete binary tree part and $O(\lg n+\sqrt{n\lg n})$ as an upper bound on the depth of each of the $\sqrt{n\lg n}$ nodes in the protruding chain. Thus, the average depth of a node is bounded from above by
$$\begin{array}{rl}\frac{1}{n}\cdot O(\sqrt{n\lg n}(\lg n+\sqrt{n\lg n})+(n-\sqrt{n\lg n})\lg n)& =\frac{1}{n}\cdot O(n\lg n)\\ & =O(\lg n).\end{array}$$
To bound the average depth of a node from below, observe that the bottommost level of the complete binary tree part has $\Theta (n-\sqrt{n-\lg n})$ nodes, and each of these nodes has depth $\Theta (\lg n)$. Thus, the average node depth is at least
$$\begin{array}{rl}\frac{1}{n}\cdot \Theta ((n-\sqrt{n-\lg n})\lg n)& =\frac{1}{n}\cdot \Omega (n\lg n)\\ & =\Omega (\lg n).\end{array}$$
Because the average node depth is both $O(\lg n)$ and $\Omega (\lg n)$, it is $\Theta (\lg n)$.

12.4-3

证明：当$n=3$时，共有5种二叉搜索树，但排列有6种。

12.4-4

略。

12.4-5

证明（来自参考答案）：
Let $A(n)$ denote the probability that when quicksorting a list of length $n$, some pivot is selected to not be in the middle $n^{1-k/2}$ of the numberes. This doesn’t happen with probability $\frac{1}{n^{k/2}}$. Then, we have that the two subproblems are of size $n_1,n_2$ with $n_1+n_2=n-1$, then
$$A(n)\le \frac{1}{n^{k/2}}+T(n_1)+T(n_2).$$
Since we bounded the depth by $O(1/\lg n)$ let ${a_{i,j}}_i$ be all the subproblem sizes left at depth $j$,
$$A(n)\le \frac{1}{n^{k/2}}\sum _j\sum _i\frac{1}{a}.$$

思考题

12-1（带有相同关键字的二叉搜索树）

a.

解：每次插入都会将元素添加到最右边的叶子的右侧，因为第11行的不等式将始终计算为false。时间复杂度为${\sum }_{i=1}^{n}i\in \Theta (n^2)$。

b.

解：这种策略将导致两个子树中的每个子树的大小最多只有一个。这意味着高度将是$\Theta (\lg n)$。因此，总运行时间为${\sum }_{i=1}^n\lg n\in \Theta (n\lg n)$。

c.

解：只需要线性时间，因为树本身的高度为$0$，单个插入列表可以在恒定时间内完成。

d.

解：
最坏情况：每个随机选择都在右侧（或全部在左侧），这将导致与此问题的第一部分相同的行为，$\Theta (n^2)$。
期望运行时间：当随机选择时，树将大致平衡，因此深度大致为$\lg (n)$，$\Theta (n\lg n)$。

12-2（基数树）

思路：对类似图12-5的树进行前序遍历即可。

12-3（随机构建二叉搜索树中的平均结点深度）

a.

易证。

b.

证明：$T_L$和$T_R$一共有n-1个元素，每个元素的深度相对于T来说都少了1，而T的根结点深度为0。

c.

证明思路：把i看成左子树的元素个数易证。

d.

证明思路：因为$P(0)=0$，又因为对称性易证。

e.

证明（来自参考答案）：
Observe that if, in the recurrence $\text{(7.6)}$ in part © Problem 7-3, we replace $\text{E}[T(\cdot )]$ by $P(\cdot )$ and we replace $q$ by $k$, we get almost the same recurrence as in part (d) of Problem 12-3. The remaining difference is that in Problem 12-3(d), the summation starts at $1$ rather than $2$. Observe, however, that a binary tree with just one node has a total path length of $0$, so that $P(1)=0$. Thus, we can rewrite the recurrence in Problem 12-3(d) as
$$P(n)=\frac{2}{n}\sum _{k=2}^{n-1}P(k)+\Theta (n)$$
and use the same technique as was used in Problem 7-3 to solve it.
We start by solving part (d) of Problem 7-3: showing that
$$\sum _{k=2}^{n-1}k\lg k\le \frac{1}{2}{n}^2\lg n-\frac{1}{8}{n}^2.$$
Following the hint in Problem 7-3(d), we split the summation into two parts:
$$\sum _{k=2}^{n-1}k\lg k=\sum _{k=2}^{\lceil n/2\rceil -1}k\lg k+\sum _{k=\lceil n/2\rceil }^{n-1}k\lg k.$$
The $\lg k$ in the first summation on the right is less than $\lg (n/2)=\lg n-1$, and the $\lg k$ in the second summation is less than $\lg n$. Thus,
$$\begin{array}{rl}\sum _{k=2}^{n-1}k\lg k& <(\lg n-1)\sum _{k=2}^{\lceil n/2\rceil -1}k+\lg n\sum _{k=\lceil n/2\rceil }^{n-1}k\\ & =\lg n\sum _{k=2}^{n-1}k-\sum _{k=2}^{\lceil n/2\rceil -1}k\\ & \le \frac{1}{2}n(n-1)\lg n-\frac{1}{2}(\frac{n}{1}-1)\frac{n}{2}\\ & \le \frac{1}{2}{n}^2\lg n-\frac{1}{8}{n}^2\end{array}$$
if $n\ge 2$.
Now we show that the recurrence
$$P(n)=\frac{2}{n}\sum _{k=2}^{n-1}P(k)+\Theta (n)$$
has the solution $P(n)=O(n\lg n)$. We use the substitution method. Assume inductively that $P(n)\le an\lg n+b$ for some positive constants $a$ and $b$ to be determined. We can pick $a$ and $b$ sufficiently large so that $an\lg n+b\ge P(1)$. Then, for $n>1$, we have by substitution
$$\begin{array}{rl}P(n)& =\frac{2}{n}\sum _{k=2}^{n-1}P(k)+\Theta (n)\\ & \le \frac{2}{n}\sum _{k=2}^{n-1}(ak\lg k+b)+\Theta (n)\\ & =\frac{2a}{n}\sum _{k=2}^{n-1}k\lg k+\frac{2b}{n}(n-2)+\Theta (n)\\ & \le \frac{2a}{n}(\frac{1}{2}{n}^2\lg n-\frac{1}{8}{n}^2)+\frac{2b}{n}(n-2)+\Theta (n)\\ & \le an\lg n-\frac{a}{4}n+2b+\Theta (n)\\ & =an\lg n+b+(\Theta (n)+b-\frac{a}{4}n)\\ & \le an\lg n+b,\end{array}$$
since we can choose $a$ large enough so that $\frac{a}{4}n$ dominates $\Theta (n)+b$. Thus, $P(n)=O(n\lg n)$.

f.

我们在将元素插入二叉搜索树的子树和在快速排序中对子序列进行排序之间进行类比。注意，一旦元素$x$被选为子树$T$的根，所有将在$x$之后插入$T$的元素将被比作$x$。 类似地，观察一旦元素$y$被选为子元素$S$中的主元，$S$中的所有其他元素将被拿来与$y$比较。因此，比较与插入二叉搜索树时所做的比较相同的快速实现只是按照与元素插入树中的顺序相同的顺序来考虑主元。

12-4（不同二叉树的数目）

a.

证明思路：先确定根结点（n种等可能），左右子树的元素数就确定了，再分别对左右子树进行类似分析。

b.

解：
$$\begin{array}{rl}B(x{)}^2& =(b_0{x}^0+b_1{x}^1+b_2{x}^2+\cdots {)}^2\\ & =b_0^2{x}^0+(b_0{b}_1+b_1{b}_0)x^1+(b_0{b}_2+b_1{b}_1+b_2{b}_0)x^2+\cdots \\ & =\sum _{k=0}^0{b}_k{b}_{0-k}{x}^0+\sum _{k=0}^1{b}_k{b}_{1-k}{x}^1+\sum _{k=0}^2{b}_k{b}_{2-k}{x}^2+\cdots \end{array}$$
$$\begin{array}{rl}xB(x{)}^2+1& =1+\sum _{k=0}^0{b}_k{b}_{1-1-k}{x}^1+\sum _{k=0}^2{b}_k{b}_{2-1-k}{x}^3+\sum _{k=0}^2{b}_k{b}_{3-1-k}{x}^2+\cdots \\ & =1+b_1{x}^1+b_2{x}^2+b_3{x}^3+\cdots \\ & =b_0{x}^0+b_1{x}^1+b_2{x}^2+b_3{x}^3+\cdots \\ & =\sum _{n=0}^{\infty }{b}_n{x}^n\\ & =B(x).\end{array}$$
$$\begin{array}{rl}xB(x{)}^2+1& =x\cdot \frac{1}{4x^2}(1+1-4x-2\sqrt{1-4x})+1\\ & =\frac{1}{4x}(2-2\sqrt{1-4x})-1+1\\ & =\frac{1}{2x}(1-\sqrt{1-4x})\\ & =B(x).\end{array}$$

c.

设$f(x)=\sqrt{1-4x}$，导数的分子是
$$\begin{array}{rl}2\cdot (1\cdot 2)\cdot (3\cdot 2)\cdot (5\cdot 2)\cdots & =2^k\cdot \prod _{i=0}^{k-2}(2k+1)\\ & =2^k\cdot \frac{(2(k-1))!}{2^{k-1}(k-1)!}\\ & =\frac{2(2(k-1))!}{(k-1)!}.\end{array}$$
$$f(x)=1-2x-2x^2-4x^3-10x^4-28x^5-\cdots .$$
系数是$\frac{2(2(k-1))!}{k!(k-1)!}$.
$$\begin{array}{rl}B(x)& =\frac{1}{2x}(1-f(x))\\ & =1+x+2x^2+5x^3+14x^4+\cdots \\ & =\sum _{n=0}^{\infty }\frac{(2n)!}{(n+1)!n!}x\\ & =\sum _{n=0}^{\infty }\frac{1}{n+1}\frac{(2n)!}{n!n!}x\\ & =\sum _{n=0}^{\infty }\frac{1}{n+1}\left(\genfrac{}{}{0ex}{}{2n}{n}\right)x.\end{array}$$
$$b_n=\frac{1}{n+1}\left(\genfrac{}{}{0ex}{}{2n}{n}\right).$$

d.

$$\begin{array}{rl}{b}_n& =\frac{1}{n+1}\frac{(2n)!}{n!n!}\\ & \approx \frac{1}{n+1}\frac{\sqrt{4\pi n}(2n/e{)}^{2n}}{2\pi n(n/e{)}^{2n}}\\ & =\frac{1}{n+1}\frac{4^n}{\sqrt{\pi n}}\\ & =(\frac{1}{n}+(\frac{1}{n+1}-\frac{1}{n}))\frac{4^n}{\sqrt{\pi n}}\\ & =(\frac{1}{n}-\frac{1}{n^2+n})\frac{4^n}{\sqrt{\pi n}}\\ & =\frac{1}{n}(1-\frac{1}{n+1})\frac{4^n}{\sqrt{\pi n}}\\ & =\frac{4^n}{\sqrt{\pi }{n}^{\frac{3}{2}}}(1+O(1/n)).\end{array}$$