0x0a算法设计与分析复习（三）：求解困难问题

参考书籍：算法设计与分析——C++语言描述（第二版）

求解困难问题

NP完全问题

多项式时间算法: 对规模为n的输入，它们在最坏情况下的运行时间为O(nk)，k为常数。

指数时间算法：对规模为n的输入，它们在最坏情况下的运行时间为O(kn)。（由回溯法和分枝限界法所生成的算法，大多是指数阶。比如，0/1背包问题等）

一般，将能在多项式时间内求解的问题看做易处理问题（tractable problem），而将至今尚未找到的多项式时间算法求解的问题视为难处理问题（intractable problem）。

对于难处理问题，虽然至今尚未有人给出它们的多项式时间算法，但也同样未能证明对于此类问题不存在多项式时间算法。经过研究，发现这类难解问题在计算上是相关的，被称为NP难度或NP完全问题。关于这类问题的有意义的结论是：一个NP完全问题可以在多项式时间内求解，当且仅当所有其他的NP完全问题都可以在多项式时间内求解。如果任意一个NP难度问题存在一个多项式时间算法，那么所有NP完全问题都可以在多项式时间内求解。

还有一类问题被称为不可判定（undecidable）的，无论消耗多少计算机时间和空间也不能求解。所谓“停机”问题就是不可解的。

不确定算法和不确定机

抽象机模型：设抽象机提供由m个基本运算（也可称为语句）组成的运算集O=O1,O2,⋯,Om，每个运算都是基本的，它们的执行时间是有限常量。同时设执行第i个运算Oi所需的时间是αi，1≤i≤m。

一个算法对于给定的输入在抽象机上的一次执行过程，表现为执行一个基本运算序列。

不确定算法的抽象机模型

为便于研究，先假定一种运行不确定算法的抽象计算模型，它除了包含抽象机模型的基本运算外，最根本的区别在于它新增了下面一个新函数和两个新语句：

• Choice(S): 任意选择集合S的一个元素；
• Failure: 发出不成功完成信号后算法终止；
• Success: 发出成功完成信号后算法终止。

包含Choice函数的算法能按如下既定方式执行：

• 当算法执行中需作出一系列的Choice函数选择时，当且仅当对于Choice的任何一组选择都不会导致成功信号时，此算法在O(1)时间失败终止；
• 否则, 只要存在一组选择能够导致成功时, 算法总能采取该组选择使得算法成功终止。

不确定机(non deterministic machine):包含不确定选择语句，并能按上述方式执行一个算法的机器。
不确定算法(non deterministic algorithm): 在不确定机上执行的算法。

不确定算法时间复杂度

定义：个不确定算法所需的时间是指对任意一个输入，当存在一个选择序列导致成功完成时，达到成功完成所需的最少程序步。在不可能成功完成的情况下，所需时间总是O(1)。

P类和NP类问题

定义（P类和NP类）：P是所有可以在多项式时间内用确定算法求解的判定问题的集合。NP是所有可在多项式时间内用不确定算法求解的判定问题的集合。

因为确定算法只是不确定算法当Choice函数只有一种选择时的特例，所以有P⊆NP。但计算机科学界至今无法断定是否P=NP或者P≠NP。

定义（多项式约化）：令Q1和Q2是两个问题，如果存在一个确定算法A求解Q1，而算法A以多项式时间调用另一个求解Q2的确定算法B。若不计B的工作量，算法A是多项式时间的，则称Q1约化（reduce to）为Q2，记做Q1∝Q2。

这就是说，求解Q1的确定算法是通过调用求解Q2的确定算法完成的，Q1算法自身及对Q2算法实施的调用过程所需的时间都是多项式时间的，那么只要对问题Q2存在多项式时间求解算法，问题Q1就能在多项式时间内得以求解。

对于约化存在以下性质：

• 性质1：若Q1∈P，Q2∝Q1,则有Q2∈P。
• 性质2（约化的传递性）：若Q1∝Q2，Q2∝Q3,则有Q1∝Q3。

NP难度和NP完全问题

NP难度：对于问题Q以及任意问题Q1∈NP，都有Q1∝Q，则称Q是NP难度（NP hard）的。

NP完全：对于问题Q∈NP，Q是NP难度的，则称Q是NP完全（NP complete）的。

上面定义表明一个问题是NP难度的，但不一定是NP完全的。一个NP难度问题，如果不是NP类问题，则不是NP完全的。所有NP完全问题都是NP难度的，反之不然。

根据性质1和NP难度问题的定义可以知道，只要对任何一个NP难度问题Q，找到它的多项式时间算法，那么，可以断定所有NP类问题都能在多项式时间内求解，因为所有的NP类问题都能约化到问题Q。

一般证明某个问题Q是NP难度的，证明策略由以下两步组成：

1. 选择一个已经证明是NP难度问题Q1
2. 求证Q1∝Q

由于Q1是NP难度的，因此所有NP类问题都可以约化到Q1，根据约化的传递性，任何NP类问题都可以约化到Q，所以Q是NP难度的。

如果进一步表明Q本身是NP类的，则问题Q是NP完全的。

Cook定理

可满足性问题（satisfiability problem）是一个判定问题，它确定对于一个给定的命题公式，是否存在布尔变量的一种赋值（也称真假指派）使该公式为真。CNF可满足性是指判定一个CNF公式的可满足性。（CNF：conjunctive normal form，合取范式）

定理：（Cook定理）可满足性问题在P中，当且仅当P=NP。

定理：CNF可满足性问题是NP完全的。

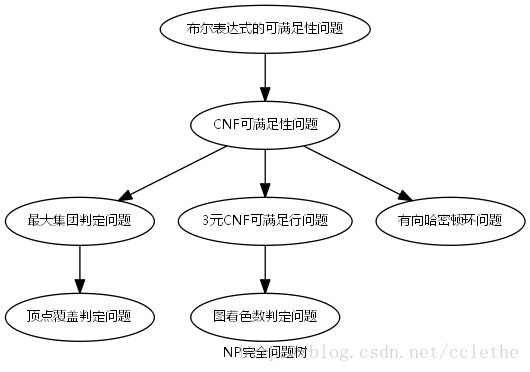
一些典型的NP完全问题

证明一个问题Q是NP难度（或NP完全）问题的具体步骤：

1. 选择一种已知的具有NP难度的问题Q1；
2. 证明能够从Q1的一个实例I1，在多项式时间内构造Q的一个实例I；
3. 证明能够在多项式时间内从I的解确定I1的解；
4. 从2和3可知，Q1∝Q；
5. 由1和4及约化的传递性得出所有的NP类问题均可约化到Q，所以Q是NP难度的；

6. 如果Q是NP类问题，则Q是NP完全的。

   • 最大集团问题
   • 定理：CNF可满足性∝最大集团判定问题。
   • 顶点覆盖
   • 最大集团判定问题∝顶点覆盖判定问题。
   • 3元CNF可满足性
   • CNF可满足性∝3元CNF可满足性。
   • 图的着色数
   • 3元CNF可满足性∝着色数判定问题。
   • 有向哈密顿环
   • CNF可满足性问题∝有向哈密顿环问题
   • 恰切覆盖
   • 3-可着色问题∝恰切覆盖问题
   • 分划问题
   • 子集和数问题∝分划问题

小结

Cook定理证明了（CNF）可满足性问题是NP完全的，所有NP类问题都可以约化到可满足性问题。

CNF可满足性∝最大集团判定问题∝顶点覆盖判定问题，CNF可满足性∝3元CNF可满足性∝着色数判定问题∝恰切覆盖问题∝子集和数问题∝分划问题，CNF可满足性问题∝有向哈密顿环问题。还可以证明子集和数问题∝0/1背包问题，有向哈密顿环问题∝旅行商问题，分划问题∝非抢先调度最小完成时间，顶点覆盖判定问题∝集合覆盖问题等。

如果一个问题一经证明是NP难度的，可不必致力于寻找多项式时间算法，而采取其他多种算法设计策略，例如：启发式算法、局部寻优、随机算法和近似算法、演化算法和神经网络等。

随机算法

基本概念

非形式地，一个随机算法（randomized algorithm）是指需要利用随机数发生器地算法，算法执行地某些选择依赖于随机数发生器所产生地随机数。由于一个随机数发生器地输出，对于算法的某一次执行而言是不可预见的，因而对所求解问题地同一实例，使用同一个随机算法地两次求解，可能得到不同地结果。

最简单地伪随机数序列可以使用线性同余法（linear congruential method）产生，即

{x0=dxn=(axn−1+c)modm, n=1,2,⋯

式中， m>0， 0≤a<m， 0≤c<m， 0≤d<m。m是模，a是乘数，c是增量，d称为该随机序列地种子。当a，c，m给定后，不同地d将产生不同地随机数序列。

随机性以不同地形式应用于随机算法中，随机算法通常分为4类：数值随机算法，蒙特卡洛算法，拉斯维加斯算法和舍伍德算法。

数值随机算法（numerical randomized algorithm）用于求数值问题的近似解。

蒙特卡洛算法（Monte Carlo-algorithm）用于求解问题的准确解。蒙特卡洛算法不保证所求的的解是正确的，也就是说，蒙特卡洛算法求得的解有时是错误的，可以设法控制这类算法得到错误解的概率。在一般情况下，蒙特卡洛算法得到正确解的概率随时间的增加而增大。但其不能确保解的正确性，而且通常无法有效地判断所求得的解究竟是否正确，这是蒙特卡洛算法的缺陷。

拉斯维加斯算法（Las Vegas-algorithm）求得的解总是正确的，但有时拉斯维加斯算法可能始终找不到解。使用拉斯维加斯算法求解同一个问题时，能够得到相同的结果，但算法的执行时间会不一样。一般情况下，求得正确解的概率随计算时间的增加而增大。

舍伍德算法（Sherwood-algorithm）总能求得问题的正确解。当一个确定性算法在最坏情况下的计算复杂度与其在平均情况下的计算复杂度两者相差较大时，可以在这个确定性算法中引入随机性将它改造成一个舍伍德算法，用来消除或减少问题的不同实例之间的这种在计算时间上的差别。舍伍德算法的精髓不是避免算法的最坏情况行为的发生，而是设法消除这种最坏行为与特定实例之间的关联性。

近似算法

基本概念

定义（近似算法）：求解最优化问题P的一个近似算法，以P的某个实例I∈DP为输入，得到问题的一个可行解σ∈SP(I)。一般要求一个近似算法的执行时间时多项式的。

绝对性能保证

定义（绝对近似算法）：绝对近似算法（absolute approximation algorithm）是求解问题P的一个多项式时间算法，使得存在常数k>0，对P的所有实例I，都有绝对误差（absolute error）|OPT(I)−F(I)|≤k。

只有极少数NP难度最优化问题存在绝对近似算法，其中之一为平面图着色问题。

相对性能保证

定义：算法A的比值界（ratio bound）定义为

max{F(I)/OPT(I),OPT(I)/F(I)}≤ρ(n)

比值 {F(I)/OPT(I)(最小化问题)或 OPT(I)/F(I)（最大化问题）称为性能比（performance ratio）。

定义：算法A是一个ϵ(n)−近似算法，当且仅当问题P的每一个实例I，都有相对误差

|OPT(I)−F(I)|/OPT(I)≤ϵ(n)

式中， ϵ(n)称为相对误差界（relative error bound）。

定义：对于某个常数ϵ，|OPT(I)−F(I)|/OPT(I)≤ϵ，则算法A被称为ϵ−近似算法。

近似方案

定义：一个近似方案（approximation scheme）A(ϵ)是一种近似算法，对于任意固定的ϵ>0和问题实例I，A(ϵ)产生一个可行解，使得|OPT(I)−F(I)|/OPT(I)≤ϵ。

定义：若对任一固定的ϵ>0，一个近似方案的运行时间是问题实例规模n的多项式，则称其为多项式时间近似方案（polynomial time approximation scheme）。

定义：如果对任一固定的ϵ>0和问题实例规模n，一个近似方案的运行时间是1/ϵ和n两者的多项式，则称其为完全多项式时间近似算法（fully polynomial time approximation scheme）。

密码算法

转载于:https://www.cnblogs.com/born2run/p/9581362.html