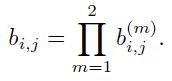多目标跟踪deepSORT
文章对论文中的翻译做了一些笔记,方便在算法使用过程中遇到问题时查看
SOART重点关注简单有效,deepSOART集成了外观信息来提高SOART的性能。能够长时跟踪被遮挡的对象,减少了标识转换的数量。本着原始框架的精神,作者将大部分复杂的计算性放入离线的预训练阶段,在此阶段,我们学习了大规模人员重新识别数据集上的深度关联度量。在在线应用过程中,算法在视觉外观空间中使用最近邻查询建立度量跟踪关联。最终减少了45%的标识转换数量。
通过检测进行跟踪已成为目标跟踪的主流。基于这种框架,目标轨迹通常出现在一个同时处理整个视频批次的全局优化问题中。但在批处理的方法不适合使用到在线应用场景中。更传统的方法是多假设跟踪(MHT)与联合概率数据过滤(JPDAF),这些方法在逐帧的基础上执行数据关联。在JPDAF中,单个状态假设是通过关联概率对单个测量值进行加权而产生的。在MHT中,所有可能的假设都被跟踪,但为了计算的可操作性,必须应用剪枝方案。这些方法的性能取决于计算量和实现复杂性。
SOART是一个非常简单的框架,卡尔曼滤波计算图像空间和逐帧数据的关联,使用匈牙利算法计算边界框重叠的关联度量。这种方法在高帧速率的视频场景下具有良好的性能,强调了目标检测器性能对整体跟踪结果的影响。
虽然SOART在跟踪精度和精度方面取得了总体良好的性能,但它返回的标识转换数量相对较高。这是因为所使用的关联度量只有在状态估计不确定性较低时才准确。因此SOART在处理遮挡的问题时效果不好。特别是使用了一个训练过的卷积神经网络(CNN)。 deepSOART使用一个结合了运动和外观信息的度量来替换关联度量(深度关联),从而克服了这个问题。通过集成该网络,deepSOART提高了对遗漏和闭塞的鲁棒性,同时保持系统易于实现,高效,适用于在线场景。
深度关联度量:
轨道处理和卡尔曼滤波框架与SOART中的原始公式基本相同。我们假设一个非常普遍的跟踪场景,在这个场景中,相机没有校准,我们没有可用的自我运动信息。正种场景是现实中最常见的。我们的跟踪场景是在八维状态空间种,包含目标框的中心位置(u,v)、宽高比r、高h及其各自在图像坐标中的速度。采用标准的等速度运动卡尔曼滤波器和线性观测模型,取边界坐标(u,v,r,h)作为对物体状态的直接观测值。
对于每个目标的轨道k,我们计算自上次成功测量关联ak以后的帧数。该计数器(帧数)在卡尔曼滤波预测期间递增,当跟踪轨迹与目标检测成功关联(IOU值大于最小阈值)时重置为0。计数器的值超过预先定义的最大阈值Amax后,目标被认为已经离开现场,并从目标轨道集删除。对于不能与现有目标轨迹关联的每个被检测到的目标,都会初始化一个新的初始假设轨迹(检验虚假检测)。这些轨迹的前3帧被归类为试探性轨迹。在此期间(3个帧),我们期望在每个时间步骤(每一帧)中都有一个成功的度量关联。新目标轨迹的前三帧若没有成功关联,那么这个目标轨迹将被删除。
指派问题(匈牙利算法):
传统解决现有目标的结果(检测框)与卡尔曼预测结果(预测框)之间关联的方式是构建一个指派问题,该问题可以用匈牙利算法解决。在解决这个问题的工程中,我们整合了运动和外观信息。
为了整合运行信息,我们使用马氏距离来度量目标检测值和卡尔曼预测值直接的距离。
其中表示由(yi,Si)将目标的第i个轨迹分布投影到测量空间,由dj检测第j个边界框。马氏距离通过测量检测到的多个偏离平均轨道位置的标准差,将状态估计的不确定性考虑在内。标准偏差检测距离(马氏距离)的平均轨迹更远,使用这个度量,可以通过在反卡方分布计算的95%置信区间内,以马氏距离作为阈值来排除不太可能的关联。
如果第i个目标轨道预测值(预测框)和第j个目标检测值(检测框)值之间的关联(马氏距离)小于一定的阈值,那么它的值为1。对于我们的四维测量空间,对应的马氏阈值为t(1) = 9.4877。
当运动不确定性较低时,马氏距离是一个合适的关联度量,而在我们的图像空间问题公式中,卡尔曼滤波框架得到的预测状态分布只能粗略估计目标位置。特别是,不明原因的相机运动会在图像平面中引入快速位移,使得马氏距离对遮挡物体的跟踪变得很差。因此,在指派问题中我们引入了第二个度量。对于每个检测出的边界框dj,我们计算一个外观描述符rj, ||rj|| = 1。此外,我们保留一个集合Rk=![]() ,最后一个Lk=100,作为每个预测出的轨迹目标k的关联外观描述符。然后,我们的第二个度量的是外观空间中第i个预测轨迹与第j个检测之间最小的余弦距离:
,最后一个Lk=100,作为每个预测出的轨迹目标k的关联外观描述符。然后,我们的第二个度量的是外观空间中第i个预测轨迹与第j个检测之间最小的余弦距离:
同样,我们引入一个二元变量来表示根据这个度量是否关联成功:
我们在一个单独的训练数据集上为这个指标找到了一个合适的阈值。在实践中,我们使用一个预先训练的CNN来计算边界框的外观描述符。该网络的体系结构将在第2.4节中描述。
通过组合,这两个度量标准在指派问题中互相补充。一方面,马氏距离提供了基于运动的跟踪目标可能的位置信息,这对短期预测特别有用。另一方面,余弦距离考虑了外观信息,这在运动的辨别性较低的情况下,对长时间遮挡后恢复身份认证非常有效。为了构建关联问题,我们使用加权和将这两个指标结合起来
其中,如果关联在两个指标的门控区域内,我们称其为可容许关联:
通过超参数λ可以控制各指标对组合关联成本的影响。通过实验我们发现,当有大量的摄像机运动时,设置λ=0是一个合理的选择。在此设置中,仅把外观信息应用到了关联成本项中,但是这个马氏门仍然可以用于删除基于卡尔曼滤波预测出的不可能的赋值(预测出的假框)。
匹配的级联:
在全局分配问题中,我们引入了一个级联方法来解决一系列子问题,而不是求解度量到跟踪的关联。当一个目标长时间被遮挡之后,卡尔曼滤波预测的不确定性就会大大增加。假如此时两个追踪器同时竞争一个检测结果的匹配权,往往遮挡时间较长的那条轨迹的信息马氏距离协方差更小,因为这些轨迹长时间未更新,不确定性增大,协方差更大,马氏距离计算时使用了协方差的倒数。因此使得检测结果更可能和遮挡时间较长的那条轨迹相关联,这种结果会破坏追踪的持续性。级联匹配的核心思想就是由小到大按照消失时间排序进行轨迹进行匹配,保证对最近出现且小时时间最短的目标优先匹配。