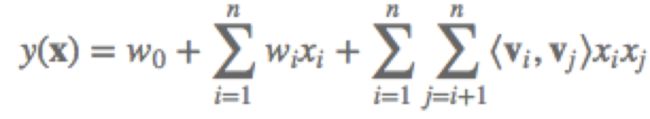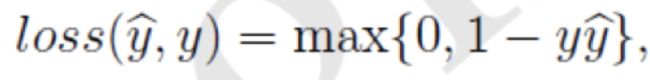FM/FFM模型 学习总结

作者：jliang

https://blog.csdn.net/jliang3

1.重点归纳

1）FM和FFM模型凭借在数据量较大并且特征稀疏的情况下，仍然能够得到优秀的性能和效果，屡次在各大公司举办的CTR预估比赛中获得不错的战绩。

2）FM旨在解决稀疏数据下的特征组合问题，使用矩阵分解的方法来求解参数，从而降低计算复杂度为线性。

（1）模型：

（2）损失函数

• 回归问题：最小平方误差（least square error）
• 二分类问题：hinge loss函数/ logit loss函数（sigmoid函数）

（3）优化方法

• 随机梯度下降法（SGD）
• 交替最小二乘法（Alternating Least-Squares, ALS）
• 马尔科夫模特卡洛算法（Markov Chain Monte Carlo, MCMC）

3）FFM在FM的基础上引入了field概率，FFM把相同性质的特征归于同一个field。

 

（1）模型：

（2）二次参数有nfk个，远多于FM模型的nk个。由于隐向量与field有关，FFM二次项不能够化简，预测复杂度是O(kn^2)

（3）损失函数采用logistic loss函数和L2惩罚项，因此只能用于二分类问题。使用SGD优化。

（4）CTR和CVR样本类别获取

• CTR预估的正样本是站内点击的用户-商品记录，负样本是展现但未点击的记录
• CVR预估的正样本是站内支付（发生转化）的用户-商品记录，负样本是点击但未转化的记录

2.FM模型

1）FM旨在解决稀疏数据下的特征组合问题

（1）对于categorical特征，一般都是进行one-hot编码处理，不可避免的样本数据变得很稀疏，另外一个问题是特征空间变得特别大。

（2）某些特征经过关联后，与label之间的相关性就会提高，因此引入两个/多个特征的组合是非常有意义的。普通的线性模型，我们都是将各个特征独立考虑的，并没有考虑到特征之间的相互关系，但实际上大量的特征之间是有关联的。

         如：女性这个特征与化妆品类服饰类商品有很大关联

（3）多项式模型是包含特征组合的最直观的模型，二阶多项式模型：

• 在数据稀疏性普遍存在的实际应用场景中，二次项参数的训练很困难，因为每个参数wij的训练需要大量xi和xj都是非零的样本。
• 矩阵分解提供了一种解决思路。

2）FM求解

（1）所有二次项参数wij可以组成一个对称阵W，这个矩阵可以分解为W=VTV。

（2）V的第j列便是第j维特征的隐向量，每个参数wij=<vi,vj>，这是FM模型的核心思想。vi是第i维特征隐向量<.,.>代表向量点积。

 

         进行简化：

（3）简化后，二次项的参数数量为kn个（计算复杂度O(kn)），远小于多项式模型的参数数量。所有包含“xi的非零组合特征”的样本都可以用来学习隐向量vi，很大程度上避免了数据稀疏性造成的影响。

3）回归和分类

（1）回归问题

• 损失函数可取最小平方误差（least square error）

（2）分类问题（二分类问题）

• 损失函数
  • hinge loss函数：
  • logit loss函数：（就是sigmoid函数）
• 为了防止过拟合，通常会在优化目标函数中加入正则项

4）优化方法

• 随机梯度下降法（SGD）
• 交替最小二乘法（Alternating Least-Squares, ALS）

每次只对一个参数进行优化，并逐轮进行迭代

• 马尔科夫模特卡洛算法（Markov Chain Monte Carlo, MCMC）

5）与SVM二阶多项式比较

• FM在样本稀疏的情况下有优势
• FM的训练/预测复杂度是线性的，SVM需要计算核矩阵，核矩阵复杂度是N^2
• MF（矩阵分解）只能局限在两类特征，SVD++与MF类似，在特征的扩展性上都不如FM

3.FFM模型

1）FFM在FM的基础上引入了field概率，FFM把相同性质的特征归于同一个field。如onehot编码前特征country下有两取值USA和China，那么onehot编码后这两个特征属于同一个field。

（1）假设样本的n个特征属于f个field，那么FFM的二次项有nf个隐向量。而在FM模型中，每一维特征的隐向量只有一个。FM可以看作是FFM的特例，是把所有特征都归属到一个field时的FFM模型。

（2）模型

• 
• C2 是非零特征的二元组合，j1 是特征，属于field f1，wj1,f2 是特征 j1 对field f2 的隐向量。

（3）二次参数有nfk个，远多于FM模型的nk个。由于隐向量与field有关，FFM二次项不能够化简，预测复杂度是O(kn^2)

2）例子

    

   那么，FFM的组合特征有10项，如下图所示。

 

其中，红色是field编号，蓝色是特征编号，绿色是此样本的特征取值。

3）损失函数采用logistic loss函数和L2惩罚项，因此只能用于二分类问题。使用SGD优化。

4）FFM应用

（1）FFM主要用来预估站内的CTR（点击率）和CVR（转化率）

• CTR和CVR预估模型都是线下训练，然后用于线上预测，采用的特征主要有三类：
  • 用户相关的特征

如：年龄、性别、职业、兴趣、品类偏好、浏览/购买品类等基础信息，用户近期点击量、购买量、消费额等统计信息。

• 商品相关的特征

如：所属品类、销量、价格、评分、历史CTR/CVR等信息。

• 用户-商品匹配特征

如：浏览/购买评论匹配、浏览/购买商家匹配、兴趣偏好匹配等几个维度。

（2）使用FFM方法，所有的特征必须转换成”field_id:feature_id:value”格式。

• 数值特征只需分配单独的field编号，如用户评论得分、商品的历史CTR/CVR等
• categorical特征需要经过one-hot编码成数值型，编码产生的所有特征同属于一个field，如用户的性别、年龄段、商品的品类id等
• 不同品类的浏览/购买数量特征，这类特征按categorical处理，不同的是特征值不是0/1，而是具体的浏览/购买数量

（3）CTR和CVR样本类别获取

• CTR预估的正样本是站内点击的用户-商品记录，负样本是展现但未点击的记录
• CVR预估的正样本是站内支付（发生转化）的用户-商品记录，负样本是点击但未转化的记录
• 模型是按天训练，每天的性能指标可能会有波动，但变化幅度不是很大

（4）FFM的实现细节

• 样本归一化。FFM默认是进行样本数据的归一化，即参数pa.norm=True，若此参数为False，很容易造成数据inf溢出，进而引起梯度计算nan错误。因此，样本层面数据推荐进行归一化。
• 特征归一化。将源数据值特征的值归一化到[0,1]是非常必要的。
• 省略零值特征。零值特征对模型完全没有贡献，包含零值特征的一次项组合项均为0，可以省去零值特征。

 

图片来源：小小挖掘机博客