2019独角兽企业重金招聘Python工程师标准>>> ![]()
计算机做加法是对人做加法的模拟。那么人是怎么做加法的呢?让我们来考察一下。
人做加法的过程
从一般的情况出发,比如怎么计算“24+35”呢?
我们把个位与个位相加,4+5=9,再把十位与十位相加,2+3=5,再合起来得到59.
这就是所谓的分而治之(divide and conque)了,用打仗的话来说,也可以说是各个击破。
显然,会做两个多位数加法的基础是会做两个一位数加法。那么,问题又来了,如何做两个一位数的加法呢?
其实,你靠的是记忆!我们会在后面再去深入探讨这一问题。
自顶向下
目前,我们考虑的是如何构造多位加法器,重点是如何去模拟多位加法器的工作过程。
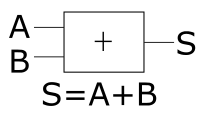
对于两个一位数加法的问题,我们暂且认为:经过反复学习,在我们的大脑中形成了一个关于一位数加法的神经网络,它的功能可由以下的一个抽象接口模型来描述:
它能接受两个一位数,并快速给出相加的结果。以此为基础,多位数的加法可以分解成多次一位数的加法,并把结果合并起来。
先不考虑一位加法器的实现细节,相反,假定它已经有了我们想要的功能,我们现在先考虑如何用它构建高级的多位加法器。
这种思路我们称之为“自顶向下(top down)”,先把目光聚焦在高层的结构上。
一位加法器是为多位加法器服务的,从服务对象考虑起能让我们更好地确定底层接口的规范。
假定底层已有我们想要的功能,这种思路又称为“wishful thinking(按愿望思维)”。它避免了我们过早地纠结在底层实现的细节上去。
关于进制与表示的问题
有人可能会想,人做加法是用十进制,计算机或者说电路做加法是用二进制,这样去类比可行吗?是不是应该先讲讲二进制的知识先呢?
进制差异自然会带来影响,特别越到底层,影响越显著。
不过,我们将看到,进制的选择暂时不会影响高层的结构。对于我们而言,十进制更加自然,到后面,会逐步转到二进制上去讨论。
至于数字的表示问题,10进制的一大麻烦就是要表示的状态太多了,既然要用电路来实现,首先很容易想到用电压来表示数字。比如数字1就用1V的电压来表示,同理,数字9就用9V来表示。
自然,这种表示不是唯一的,你也可以用0.1V来表示1,那么相应地用0.9V来表示9,关键或许在于保持这种比率关系。
两种策略
考虑前面人做加法的例子:24+35
串行
一种策略就是只用一个一位数加法器,分成多次,每一次把同一位上的两个数扔给这个一位加法器去运算:
比如先把个位的4和5扔进去,得出一个结果9,存起来;再把十位上的2和3扔进去...
当然,这种方式的挑战在于如何存储中间结果,如何依次地把数据送进去,另外还有速度的问题等等。
打造出一个如此的加法器几乎相当于一个初级计算机的雏形了。
显然,人做多位加法的过程也是串行式的。
并行
那么,一种更加简单粗暴的策略就是把几个一位加法器拼接起来,同时进行计算,一方面无需关注存储,依次送入数据等问题,另外速度上也更快了。
24+35,按照我们的习惯,左边是高位(十位),右边是低位(个位)。
如果需要更多的位数,那么简单放置更多的一位加法器就完了。这种方式需要更多的硬件,但我们也因此得到了好处。
当然了,无限的并行下去也是不行的,最终我们要的是一种中庸之道,平衡之术,盲目推崇或排斥某种方式往往都是不可取的。
比如一个32位机如何做64位的加法呢?最终还是靠串行做2次32位加法来实现。
进位的处理
当然,有一个很重要的问题被有意无意地忽略了,那就是进位。
考虑以下多位数的加法:“256+128”,
那么,通过组合三个一位数加法器,分别处理个位,十位与百位数字的相加,结果如下:
显然,3714不是我们想要的结果,因为没有考虑到进位的影响。正确的结果应该是384。
到目前为止,我们关于一位加法器的构想还是很粗糙的。首先,从最终结果的表示层面而言,按前面约定的表示,输出应该限制在0V-9V的区间。
如果是0V,按电路上一般的约定,可用一个接地符号来表示:
对于上述个位数加法而言,那么就是输入一个6V和一个8V的电压,结果输出的14V电压,这不是我们想要的结果。
显然,上述例子中,个位中只需要输出4V即可,而不是14V,14需要拆分成1和4。
现在需要修正一位加法器的原型。首先至少要两个输出,一个是加位(sum,S)的输出,一个进位(carry,C)的输出:
其次,进位的输出还要参与到下一级的输入中去,也即要有三个输入,输出则只要显示加位的结果即可:
对于右边最低位,不存在进位,使用一个接地符号表示输入为0V.
其余的进位输入则来自低位的进位输出。
图中红色的线表示产生了进位。对于中间的十位数加法,实际是5+2+1=8
经过这样的调整,多位加法器就能正常工作了,但这样一来,模型也复杂多了。
全加器
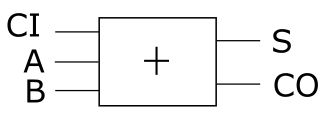
综合进位及显示的需要,那么,一个具有普遍性的一位加法器至少要三个输入,其中有一个进位输入(Carry In);以及两个输出(其中,CO指Carry out,进位输出):
这样的一个东西,我们称之为全加器(Full Adder,FA)。如果你是计算机或相关专业科班出身,你就知道为何这么叫了,我也不想引入新的叫法。
前面说到,如果从高层考虑起,能让我们更好地确定底层接口的规范,我们现在的确得到了一个更明确的接口。
如果一开始就一头猛扎进去实现最初设想的一位加法器原型,恐怕到构建多位加法器时又不得不返工了。
现在尽管我们不知道怎么去实现它,但我们却更清楚它应该是怎样的。
你心中有个Big Picture(大图景),你更加不容易走偏。
多位加法器
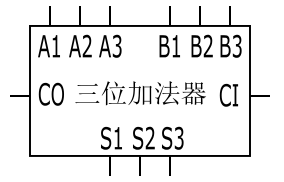
然后,以此为基础,把三个一位加法器封装在一起,把同一个数的三个位放在一起,得到以下一个三位加法器的原型:
走线就有点随意了,我也不是什么专业绘电路图的,大家能看明白原理就行了。
执行上述加法的过程如下:
通过梳理线路的走向,就无须像前面那般两个数字交叉在一起很不直观。
线未必非得要走到一块,有种说法是“接口要对用户友好”,无论你是设计硬件还是软件的接口,都应该记住这一点。
明白了它的内部实现,之后,再提到它时,只需要一个简化的接口模型:
那么,这就是搞软件的人口中所谓的抽象呀,封装呀,提供接口呀,隐藏实现呀,blabla...
模块化
以它为基础,我们又可以构建比如一个6位加法器,在它里面封装了两个三位加法器:
如果想呈现全部的细节,那么就像下面这样了,线很多,但道理还是一样的:
当然也可以跳过三位加法器,直接构建在6个全加器基础上。本质上还是一样,不过少了层封装。
自然,按照同样的思路,你还可以打造12位加法器。当然你也可以先造个2位的加法器,然后再一层一层弄出4位,8位的等等。你甚至可用一个2位加一个3位来造一个5位的加法器,有何不可呢?随便你怎么去组合。
搞软件的同学是不是又想到了什么分层次呀,模块化呀,然后又是一大堆理论,大道理,blabla...
这些原则其实是软硬通吃的。
层次性
当然,以上这些最终都建立在全加器功能的基础上。
而后面我们将看到,全加器它又是建立在半加器等的基础之上。
构造一层又一层的抽象,这就是我们应付复杂性的重要手段。
当不知道全加器是如何工作时,我们可能会觉得不够踏实,似乎一切建立在无源之水,无本之木之上一样。我们将在下一篇再探讨如何去构建全加器。见计算机是如何做加法的?(2)——构建一位加法器