小波变换在图像融合上的应用
1.DWT2是二维单尺度小波变换,其可以通过指定小波或者分解滤波器进行二维单尺度小波分解。
而WAVEDEC2是二维多尺度小波分解。
DWT2的一种语法格式是[cA,cH,cV,cD]=dwt2(X,'wname');
而对应的WAVEDEC2的语法格式是[C,S]=wavedec2(X,N,'wname'),其中N为大于1的正整数。
也就是说DWT2只能对某个输入矩阵X进行一次分解,而WAVEDEC2可以对输入矩阵X进行N次分解。
2.wavedec2:多层二维离散小波变换函数
[C,S] = wavedec2(X,N,'wname')
[C,S] = wavedec2(X,N,Lo_D,Hi_D)
appcoef2:二维离散小波变换低频部分系数提取
A = appcoef2(C,S,'wname',N)
A = appcoef2(C,S,'wname')
A = appcoef2(C,S,Lo_R,Hi_R)
A = appcoef2(C,S,Lo_R,Hi_R,N)
3.detcoef2:二维离散小波变换高频部分系数提取
D = detcoef2(O,C,S,N)
转载于:https://www.cnblogs.com/xfzhang/p/7295041.html
4.
wavedec2函数:
1.功能:实现图像(即二维信号)的多层分解.
多层,即多尺度.
2.格式:[c,s]=wavedec2(X,N,'wname')
[c,s]=wavedec2(X,N,Lo_D,Hi_D)(我不讨论它)
3.参数说明:对图像X用wname小波基函数实现N层分解,
这里的小波基函数应该根据实际情况选择,具体选择办法可以搜之.输出为c,s.
c为各层分解系数,s为各层分解系数长度,也就是大小.
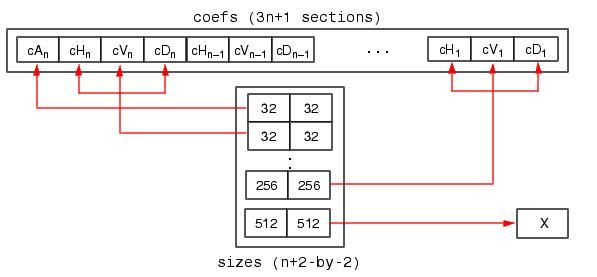
4.c的结构:c=[A(N)|H(N)|V(N)|D(N)|H(N-1)|V(N-1)|D(N-1)|H(N-2)|V(N-2)|D(N-2)|...|H(1)|V(1)|D(1)]
可见,c是一个行向量,即:1*(size(X)),(e.g,X=256*256,then c大小为:1*(256*256)=1*65536)
A(N)代表第N层低频系数,H(N)|V(N)|D(N)代表第N层高频系数,分别是水平,垂直,对角高频,以此类推,到H(1)|V(1)|D(1).
s的结构:是储存各层分解系数长度的,即第一行是A(N)的长度,第二行是H(N)|V(N)|D(N)|的长度,第三行是
H(N-1)|V(N-1)|D(N-1)的长度,倒数第二行是H(1)|V(1)|D(1)长度,最后一行是X的长度(大小)
那么S有什么用呢?
s的结构:是储存各层分解系数长度的,即第一行是A(N)的长度(其实是A(N)的原矩阵的行数和列数),
第二行是H(N)|V(N)|D(N)|的长度,
第三行是
H(N-1)|V(N-1)|D(N-1)的长度,
倒数第二行是H(1)|V(1)|D(1)长度,
最后一行是X的长度(大小)
从上图可知道:cAn的长度就是32*32,cH1、cV1、cD1的长度都是256*256。
到此为止,你可能要问C的输出为什么是行向量?
1、没有那一种语言能够动态输出参数的个数,更何况C语言写的Matlab
2、各级详细系数矩阵的大小(size)不一样,所以不能组合成一个大的矩阵输出。
因此,把结果作为行向量输出是最好,也是唯一的选择。
转载自http://maiqiuzhizhu.blog.sohu.com/110325150.html