机器学习实战刻意练习 —— Task 02. 逻辑回归
第 1 周任务
分类问题:K-邻近算法
分类问题:决策树
第 2 周任务
分类问题:朴素贝叶斯
分类问题:逻辑回归
第 3 周任务
分类问题:支持向量机
第 4 周任务
分类问题:AdaBoost
第 5 周任务
回归问题:线性回归、岭回归、套索方法、逐步回归等
回归问题:树回归
第 6 周任务
聚类问题:K均值聚类
相关问题:Apriori
第 7 周任务
相关问题:FP-Growth
第 8 周任务
简化数据:PCA主成分分析
简化数据:SVD奇异值分解
文章目录
-
- 1.简介
-
- 1.1. Logistic回归
-
- Sigmoid函数
- 极大似然推导
- 1.2.梯度上升法
- 2. 动手实战
-
- 2.1. 项目案例:预测患疝气病的马的存活问题
- 参考资料
1.简介
logistic回归又称logistic回归分析,是一种广义的线性回归分析模型,常用于数据挖掘,疾病自动诊断,经济预测等领域。例如,探讨引发疾病的危险因素,并根据危险因素预测疾病发生的概率等。以胃癌病情分析为例,选择两组人群,一组是胃癌组,一组是非胃癌组,两组人群必定具有不同的体征与生活方式等。因此因变量就为是否胃癌,值为“是”或“否”,自变量就可以包括很多了,如年龄、性别、饮食习惯、幽门螺杆菌感染等。自变量既可以是连续的,也可以是分类的。然后通过logistic回归分析,可以得到自变量的权重,从而可以大致了解到底哪些因素是胃癌的危险因素。同时根据该权值可以根据危险因素预测一个人患癌症的可能性。
1.1. Logistic回归
Logistic回归是众多分类算法中的一员。通常,Logistic回归用于二分类问题,例如预测明天是否会下雨。当然它也可以用于多分类问题,不过为了简单起见,本文暂先讨论二分类问题。首先,让我们来了解一下,什么是Logistic回归。
首先考虑线性分类器z = w_0 + w_1x_1 +……+ w_kx_k,为了进行分类任务,利用sigmoid函数将z映射为概率进行分类。Logistic回归通过假设每个事件服从伯努利分布(1,p),而p则受sigmoid函数控制。根据伯努利分布,可写出每个事件的概率分布,再利用极大似然法可求出参数w_1…w_k,下面分别讨论每一个步骤
Sigmoid函数
Logistic回归中的sigmoid函数形式如下

其中

若利用概率将其写成一个等式来描述y的分布,即 p ( y ) = g ( z ) y ( 1 − g ( z ) ) 1 − y p(y) = g(z)^y(1-g(z))^{1-y} p(y)=g(z)y(1−g(z))1−y
Sigmoid函数有一些特性,其导数如下
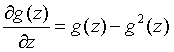
极大似然推导
假设每个事件 b ( 1 , g ( z i ) ) b(1,g(z_i)) b(1,g(zi)),则根据上文 p ( y i ) = g ( z i ) y i ( 1 − g ( z i ) ) 1 − y i p(y_i) = g(z_i)^{y_i}(1-g(z_i))^{1-y_i} p(yi)=g(zi)yi(1−g(zi))1−yi,由此可求出似然函数L(w)
L ( w ) = ∏ i = 1 n g ( z i ) y i ( 1 − g ( z i ) ) 1 − y i L(w) = \prod_{i=1}^n g(z_i)^{y_i}(1-g(z_i))^{1-y_i} L(w)=i=1∏ng(zi)yi(1−g(zi))1−yi
取对数求得对数似然函数l(w)
l ( w ) = ∑ i = 1 n y i l n g ( z i ) + ∑ i = 1 n ( 1 − y i ) l n ( 1 − g ( z i ) ) ) l(w) = \sum_{i=1}^ny_iln g(z_i) + \sum_{i=1}^n (1-y_i)ln (1-g(z_i))) l(w)=i=1∑nyilng(zi)+i=1∑n(1−yi)ln(1−g(zi)))
对每个 w j w_j wj求其偏导可得
∂ l ( w ) ∂ w j = ∑ i = 1 n y i ( 1 − g ( z i ) ) x i j − ∑ i = 1 n ( 1 − y i ) g ( z i ) x i j = ∑ i = 1 n ( y i − g ( z i ) ) x i j \frac{\partial l(w)}{\partial w_j} = \sum_{i=1}^ny_i(1-g(z_i))x_{ij} - \sum_{i=1}^n(1-y_i)g(z_i)x_{ij}= \sum_{i=1}^n (y_i-g(z_i))x_{ij} ∂wj∂l(w)=i=1∑nyi(1−g(zi))xij−i=1∑n(1−yi)g(zi)xij=i=1∑n(yi−g(zi))xij
可以发现,l(w)的梯度和线性回归类似,只是logistic回归是g(z)而线性回归是z。但由于这点不同导致logistic回归的似然函数写不出最大值的表达式,因此需要通过牛顿法或梯度上升来求得参数。
1.2.梯度上升法
根据上文有似然函数的梯度如下
∂ l ( w ) ∂ w j = ∑ i = 1 n ( y i − g ( z i ) ) x i j \frac{\partial l(w)}{\partial w_j} = \sum_{i=1}^n (y_i-g(z_i))x_{ij} ∂wj∂l(w)=i=1∑n(yi−g(zi))xij
写成矩阵形式即
∇ w j = ∂ l ( w ) ∂ w j = ( y − 1 1 + e − X W ) ′ x j \nabla_{w_j} = \frac{\partial l(w)}{\partial w_j} = (y-\frac{1}{1+e^{-XW}})'x_j ∇wj=∂wj∂l(w)=(y−1+e−XW1)′xj
那么根据梯度上升每个参数的更新如下,其中 α α α为梯度步长 w j : = w j + α ∇ w j w_j := w_j + \alpha \nabla_{w_j} wj:=wj+α∇wj
如此可求得Logistic回归的权重 w 1 . . . . . . w k w_1......w_k w1......wk
让我们整理一下思路,Logistic的推导思路如下
- 首先z与自变量x线性相关,为了对z进行分类,利用sigmoid函数将其映射为概率p
- 假设每个事件服从伯努利分布,则伯努利分布的参数即为p
- 由此可写出似然函数,利用极大似然估计,根据链式法则求导,再利用梯度上升求得权重 w 1 w_1 w1… w k w_k wk
2. 动手实战
2.1. 项目案例:预测患疝气病的马的存活问题
项目概述
本次实战内容,将原始数据集下载地址。
这里的数据包含了368个样本和28个特征。这种病不一定源自马的肠胃问题,其他问题也可能引发马疝病。该数据集中包含了医院检测马疝病的一些指标,有的指标比较主观,有的指标难以测量,例如马的疼痛级别。另外需要说明的是,除了部分指标主观和难以测量外,该数据还存在一个问题,数据集中有30%的值是缺失的。下面将首先介绍如何处理数据集中的数据缺失问题,然后再利用Logistic回归和随机梯度上升算法来预测病马的生死。
准备数据
数据中的缺失值是一个非常棘手的问题,很多文献都致力于解决这个问题。那么,数据缺失究竟带来了什么问题?假设有100个样本和20个特征,这些数据都是机器收集回来的。若机器上的某个传感器损坏导致一个特征无效时该怎么办?它们是否还可用?答案是肯定的。因为有时候数据相当昂贵,扔掉和重新获取都是不可取的,所以必须采用一些方法来解决这个问题。下面给出了一些可选的做法:
- 使用可用特征的均值来填补缺失值;
- 使用特殊值来填补缺失值,如-1;
- 忽略有缺失值的样本;
- 使用相似样本的均值添补缺失值;
- 使用另外的机器学习算法预测缺失值。
预处理数据做两件事:
- 如果测试集中一条数据的特征值已经确实,那么我们选择实数0来替换所有缺失值,因为本文使用Logistic回归。因此这样做不会影响回归系数的值。sigmoid(0)=0.5,即它对结果的预测不具有任何倾向性。
- 如果测试集中一条数据的类别标签已经缺失,那么我们将该类别数据丢弃,因为类别标签与特征不同,很难确定采用某个合适的值来替换。
原始的数据集经过处理,保存为两个文件:horseColicTest.txt和horseColicTraining.txt。
有了这些数据集,我们只需要一个Logistic分类器,就可以利用该分类器来预测病马的生死问题了。
开发流程
在使用Sklearn构建Logistic回归分类器之前,我们先用自己写的改进的随机梯度上升算法进行预测,先热热身。使用Logistic回归方法进行分类并不需要做很多工作,所需做的只是把测试集上每个特征向量乘以最优化方法得来的回归系数,再将乘积结果求和,最后输入到Sigmoid函数中即可。如果对应的Sigmoid值大于0.5就预测类别标签为1,否则为0。
import numpy as np
import random
"""
函数说明:sigmoid函数
Parameters:
inX - 数据
Returns:
sigmoid函数
"""
def sigmoid(inX):
return 1.0 / (1 + np.exp(-inX))
"""
函数说明:改进的随机梯度上升算法
Parameters:
dataMatrix - 数据数组
classLabels - 数据标签
numIter - 迭代次数
Returns:
weights - 求得的回归系数数组(最优参数)
"""
def stocGradAscent1(dataMatrix, classLabels, numIter=150):
m,n = np.shape(dataMatrix) #返回dataMatrix的大小。m为行数,n为列数。
weights = np.ones(n) #参数初始化 #存储每次更新的回归系数
for j in range(numIter):
dataIndex = list(range(m))
for i in range(m):
alpha = 4/(1.0+j+i)+0.01 #降低alpha的大小,每次减小1/(j+i)。
randIndex = int(random.uniform(0,len(dataIndex))) #随机选取样本
h = sigmoid(sum(dataMatrix[randIndex]*weights)) #选择随机选取的一个样本,计算h
error = classLabels[randIndex] - h #计算误差
weights = weights + alpha * error * dataMatrix[randIndex] #更新回归系数
del(dataIndex[randIndex]) #删除已经使用的样本
return weights #返回
"""
函数说明:使用Python写的Logistic分类器做预测
Parameters:
无
Returns:
无
"""
def colicTest():
frTrain = open('horseColicTraining.txt') #打开训练集
frTest = open('horseColicTest.txt') #打开测试集
trainingSet = []; trainingLabels = []
for line in frTrain.readlines():
currLine = line.strip().split('\t')
lineArr = []
for i in range(len(currLine)-1):
lineArr.append(float(currLine[i]))
trainingSet.append(lineArr)
trainingLabels.append(float(currLine[-1]))
trainWeights = stocGradAscent1(np.array(trainingSet), trainingLabels, 500) #使用改进的随即上升梯度训练
errorCount = 0; numTestVec = 0.0
for line in frTest.readlines():
numTestVec += 1.0
currLine = line.strip().split('\t')
lineArr =[]
for i in range(len(currLine)-1):
lineArr.append(float(currLine[i]))
if int(classifyVector(np.array(lineArr), trainWeights))!= int(currLine[-1]):
errorCount += 1
errorRate = (float(errorCount)/numTestVec) * 100 #错误率计算
print("测试集错误率为: %.2f%%" % errorRate)
"""
函数说明:分类函数
Parameters:
inX - 特征向量
weights - 回归系数
Returns:
分类结果
"""
def classifyVector(inX, weights):
prob = sigmoid(sum(inX*weights))
if prob > 0.5: return 1.0
else: return 0.0
if __name__ == '__main__':
colicTest()
# 测试集错误率为: 34.33%
错误率还是蛮高的,而且耗时1.9s,并且每次运行的错误率也是不同的,错误率高的时候可能达到40%多。为啥这样?首先,因为数据集本身有30%的数据缺失,这个是不能避免的。另一个主要原因是,我们使用的是改进的随机梯度上升算法,因为数据集本身就很小,就几百的数据量。用改进的随机梯度上升算法显然不合适。让我们再试试梯度上升算法,看看它的效果如何?
import numpy as np
import random
"""
函数说明:sigmoid函数
Parameters:
inX - 数据
Returns:
sigmoid函数
"""
def sigmoid(inX):
return 1.0 / (1 + np.exp(-inX))
"""
函数说明:梯度上升算法
Parameters:
dataMatIn - 数据集
classLabels - 数据标签
Returns:
weights.getA() - 求得的权重数组(最优参数)
"""
def gradAscent(dataMatIn, classLabels):
dataMatrix = np.mat(dataMatIn) #转换成numpy的mat
labelMat = np.mat(classLabels).transpose() #转换成numpy的mat,并进行转置
m, n = np.shape(dataMatrix) #返回dataMatrix的大小。m为行数,n为列数。
alpha = 0.01 #移动步长,也就是学习速率,控制更新的幅度。
maxCycles = 500 #最大迭代次数
weights = np.ones((n,1))
for k in range(maxCycles):
h = sigmoid(dataMatrix * weights) #梯度上升矢量化公式
error = labelMat - h
weights = weights + alpha * dataMatrix.transpose() * error
return weights.getA() #将矩阵转换为数组,并返回
"""
函数说明:使用Python写的Logistic分类器做预测
Parameters:
无
Returns:
无
"""
def colicTest():
frTrain = open('horseColicTraining.txt') #打开训练集
frTest = open('horseColicTest.txt') #打开测试集
trainingSet = []; trainingLabels = []
for line in frTrain.readlines():
currLine = line.strip().split('\t')
lineArr = []
for i in range(len(currLine)-1):
lineArr.append(float(currLine[i]))
trainingSet.append(lineArr)
trainingLabels.append(float(currLine[-1]))
trainWeights = gradAscent(np.array(trainingSet), trainingLabels) #使用改进的随即上升梯度训练
errorCount = 0; numTestVec = 0.0
for line in frTest.readlines():
numTestVec += 1.0
currLine = line.strip().split('\t')
lineArr =[]
for i in range(len(currLine)-1):
lineArr.append(float(currLine[i]))
if int(classifyVector(np.array(lineArr), trainWeights[:,0]))!= int(currLine[-1]):
errorCount += 1
errorRate = (float(errorCount)/numTestVec) * 100 #错误率计算
print("测试集错误率为: %.2f%%" % errorRate)
"""
函数说明:分类函数
Parameters:
inX - 特征向量
weights - 回归系数
Returns:
分类结果
"""
def classifyVector(inX, weights):
prob = sigmoid(sum(inX*weights))
if prob > 0.5: return 1.0
else: return 0.0
if __name__ == '__main__':
colicTest()
# 测试集错误率为: 28.36%
可以看到算法耗时减少了,错误率稳定且较低。很显然,使用随机梯度上升算法,反而得不偿失了。所以可以得到如下结论:
- 当数据集较小时,我们使用梯度上升算法
- 当数据集较大时,我们使用改进的随机梯度上升算法
参考资料
- https://baike.baidu.com/item/logistic%E5%9B%9E%E5%BD%92/2981575
- https://blog.csdn.net/c406495762/article/details/77723333
- https://blog.csdn.net/qq_35719435/article/details/81706140
- https://blog.csdn.net/c406495762/article/details/77851973