最小二乘法及其正则化——求导、几何、概率角度

求导角度

数据集：n个p维样本集用矩阵X表示，值Y为n维向量，W为p维向量。
$$X={\left[\begin{array}{cccc}{x}_1& x_2& ...& x_n\end{array}\right]}^T=\left[\begin{array}{c}{x}_1^T\\ x_2^T\\ ...\\ x_n^T\end{array}\right]={\left[\begin{array}{cccc}{x}_{11}& x_{12}& ...& x_{1p}\\ x_{21}& x_{22}& ...& x_{2p}\\ ...& ...& ...& ...\\ x_{n1}& x_{n2}& ...& x_{np}\end{array}\right]}_{np}$$
$$Y=\left[\begin{array}{c}{y}_1\\ y_2\\ ...\\ y_n\end{array}\right],W=\left[\begin{array}{c}{\omega }_1\\ {\omega }_2\\ ...\\ {\omega }_p\end{array}\right]$$
所以可得损失函数L：
$$\begin{gathered} L(\omega )=\sum _{i=1}^n||W^T{x}_i-Y|{|}^2=\sum _{i=1}^n(W^T{x}_i-Y{)}^T(W^T{x}_i-Y) \\ =[(W^T{x}_1,W^T{x}_2,...,W^T{x}_n)-(y_1,y_2,...,y_m)][(W^T{x}_1,W^T{x}_2,...,W^T{x}_n)-(y_1,y_2,...,y_m){]}^T \\ =(W^T{X}^T-Y^T)(W^T{X}^T-Y^T{)}^T=(W^T{X}^T-Y^T)(XW-Y) \\ =W^T{X}^{T}XW-W^T{X}^{T}Y-Y^{T}XW+Y^{T}Y \\ =W^T{X}^{T}XW-2W^T{X}^{T}Y+Y^{T}Y \end{gathered}$$
对L($\omega$)求导可得最优解$\omega$ = argmin L($\omega$) ：
$$\frac{\partial L}{\partial \omega }=2X^{T}XW-2X^{T}Y=0,即W=(X^{T}X{)}^{-1}{X}^{T}Y$$
这里默认X^TX是一个可逆矩阵。

几何角度

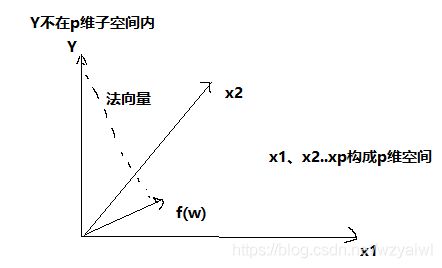
f($\omega$) =X$\omega$ ,这里将X矩阵的每一列看成一个向量，即是一个p维行向量，乘以p维列向量$\omega$ 相当于几何上的线性组合，合成一个新的向量Y，但往往因为噪声的存在，新的向量Y并不在p维子空间内。

上图的法向量等于Y- f($\omega$) = Y- X$\omega$ ，因为法向量和垂直于p维空间，所以X^T (Y- X$\omega$) = 0
所以可得：
$$\omega =(X^{T}X{)}^{-1}{X}^{T}Y$$
此结果和导数角度算出是一样的。

概率角度

这里先引入一个定理：
已知p维向量服从X~N（$\mu$，$\sum$）,Y = Ax+B，其中B为q维向量，A为qp维矩阵，Y为q维向量。
则Y~N（A$\mu$+B，A$\sum$A^T）
$$\sum =\left[\begin{array}{cccc}{\sigma }_{11}& {\sigma }_{12}& ...& {\sigma }_{1p}\\ {\sigma }_{21}& {\sigma }_{22}& ...& {\sigma }_{2p}\\ ...& ...& ...& ...\\ {\sigma }_{p1}& {\sigma }_{p2}& ...& {\sigma }_{pp}\end{array}\right],实对称矩阵$$

假设噪声$\xi$服从高斯分布，即$\xi$~N(0,$\sigma$²)，对于单个样本y = $\omega$^Tx + $\xi$ ,则y|x;$\omega$ ~N($\omega$^Tx，$\sigma$²)
即 $$P(y|x;\omega )=\frac{1}{\sqrt{2\pi }\sigma }{e}^{\frac{-(y-{\omega }^{T}x{)}^2}{2{\sigma }^2}}$$
由极大似然估计可得
$$\begin{gathered} \phi (\omega )=lnP(Y|X;\omega )=In\prod _{i=1}^{n}P(y_i|x_i;\omega )=\sum _{i=1}^{n}In\frac{1}{\sqrt{2\pi }\sigma }{e}^{\frac{-(y-{\omega }^T{x}_i{)}^2}{2{\sigma }^2}} \\ =\sum _{i=1}^n(In\frac{1}{\sqrt{2\pi }\sigma }-\frac{(y-{\omega }^T{x}_i{)}^2}{2{\sigma }^2}) \\ =nIn\frac{1}{\sqrt{2\pi }\sigma }-\frac{1}{2{\sigma }^2}\sum _{i=1}^n((y-{\omega }^T{x}_i{)}^2) \end{gathered}$$
$\omega$ = arg${\max }_{\omega }$ $\phi (\omega )$ = $nIn\frac{1}{\sqrt{2\pi }\sigma }-\frac{1}{2{\sigma }^2}{\sum }_{i=1}^n((y-{\omega }^T{x}_i{)}^2)$ = ${\sum }_{i=1}^n-(y-{\omega }^T{x}_i{)}^2$
即 $\omega$ = arg${\min }_{\omega }$ ${\sum }_{i=1}^n(y-{\omega }^T{x}_i{)}^2$
总结：最小二乘估计 $⟹$ 极大似然估计（条件是噪音服从高斯分布）

正则化

频率角度

当你数据的样本数N》维度P，就容易出现过拟合现象，在数据上的体现就是X^TX不可逆，其下面的式子也不会成立。

$$W=(X^{T}X{)}^{-1}{X}^{T}Y$$
为了解决过拟合，除了数据增强、降维，正则化也是常用的措施。
正则化框架：
$$J(\omega )=L(\omega )+\lambda P(\omega )，其中\lambda >0$$
L1范式表示P($\omega$) = ||w||¹
L2范式表示P($\omega$) = ||w||²

可知：
$$\begin{gathered} J(\omega )=L(\omega )+\lambda P(\omega )=W^T{X}^{T}XW-2W^T{X}^{T}Y+Y^{T}Y+\lambda W^{T}W \\ =W^T(X^{T}X+\lambda I)W-2W^T{X}^{T}Y+Y^{Y}Y \end{gathered}$$
则$$W=arg\underset{\omega }{\min }J(\omega )$$
对J求导可得：
$$\frac{\partial J}{\partial \omega }=2(X^{T}X+\lambda I)W-2X^{T}Y=0$$
所以可得：
$$\omega =(X^{T}X+\lambda I{)}^{-1}{X}^{T}Y$$
X^TX是一个半正定矩阵，不一定可逆，但 X^TX+$\lambda$ I一定是一个可逆矩阵，这样就解决了过拟合在数据上体现的缺陷，可清楚求出$\omega$。
下面给出 X^TX+$\lambda$ I可逆的证明：
$$\because (X^{T}X+\lambda I)x=0$$
$$\therefore X^{T}Xx=-\lambda x$$
$$\because X^{T}X是半正定矩阵,其对应特征值非负，\lambda >0$$
$$\therefore x=0,即齐次方程组有唯一零解，故X^{T}X+\lambda I满秩，故其可逆$$
下面给出A^TA是半正定的证明（为了区分变量，改证A^TA）：
$$\because X^T(A^{T}A)X=(AX{)}^{T}AX=||AX|{|}^2\ge 0$$
$$由半正定矩阵的定义：如果二次型X^{\prime }AX半正定，即对于任意不为0的实列向量X，都有X^{\prime }AX\ge 0，则实对称矩阵A称为半正定$$
$$\therefore A^{T}A是半正定矩阵$$
总结：半正定矩阵加上对角矩阵一定是一个可逆矩阵。

贝叶斯角度

f($\omega$) =x^T$\omega$，噪音$\xi$服从高斯分布，即$\xi$~N(0,$\sigma$²)，对于单个样本y = $\omega$^Tx + $\xi$ ,则y|x;$\omega$ ~N($\omega$^Tx，$\sigma$²），假设 $\omega$~N(0,${\sigma }_0$²)。
y代表已知结果，$\omega$代表原因。故先验概率为P($\omega$)，后验概率为P($\omega$|y)，由贝叶斯理论可得：
$$P(\omega |y)=\frac{P(y|\omega )P(\omega )}{P(y)}$$
其中
$$P(\omega )=\frac{1}{\sqrt{2\pi }{\sigma }_0}{e}^{\frac{-||\omega )|{|}^2}{2{\sigma }_0^2}}$$
$$P(y|\omega )=\frac{1}{\sqrt{2\pi }\sigma }{e}^{\frac{-|(y-{\omega }^{T}x{)}^2}{2{\sigma }^2}}$$
由最大后验概率可得(P(y)已知，是一个实数)：
$$\begin{gathered} \omega =arg\underset{\omega }{\max }In(P(\omega |Y))=arg\underset{\omega }{\max }In\prod _{i=1}^n(P(y|\omega )P(\omega )) \\ =arg\underset{\omega }{\max }In\prod _{i=1}^n(\frac{1}{2\pi \sigma {\sigma }_0}{e}^{-(\frac{||\omega )|{|}^2}{2{\sigma }_0^2}+\frac{|(y-{\omega }^{T}x{)}^2}{2{\sigma }^2})}) \\ =arg\underset{\omega }{\max }\sum _{i=1}^n-(\frac{||\omega )|{|}^2}{2{\sigma }_0^2}+\frac{|(y-{\omega }^{T}x{)}^2}{2{\sigma }^2}) \\ =arg\underset{\omega }{\min }\sum _{i=1}^n(\frac{||\omega )|{|}^2}{2{\sigma }_0^2}+\frac{|(y-{\omega }^{T}x{)}^2}{2{\sigma }^2}) \\ =arg\underset{\omega }{\min }\sum _{i=1}^n(\frac{||\omega )|{|}^2{\sigma }^2}{{\sigma }_0^2}+(y-{\omega }^{T}x{)}^2) \\ =arg\underset{\omega }{\min }\sum _{i=1}^n(y-{\omega }^{T}x{)}^2+\frac{{\sigma }^2}{{\sigma }_0^2}||\omega |{|}^2) \end{gathered}$$
可以看出最后的结果和频率角度加入正则化L2是一样的，其中$\lambda =\frac{{\sigma }^2}{{\sigma }_0^2}$.
总结：正则化后的最小二乘估计 $⟹$ 最大后验概率（其中噪音和权重$\omega$均服从高斯分布）

总结汇总

总结：最小二乘估计 $⟹$ 极大似然估计（条件是噪音服从高斯分布）

总结：半正定矩阵加上对角矩阵一定是一个可逆矩阵。
总结：正则化后的最小二乘估计 $⟹$ 最大后验概率（其中噪音和权重$\omega$均服从高斯分布）