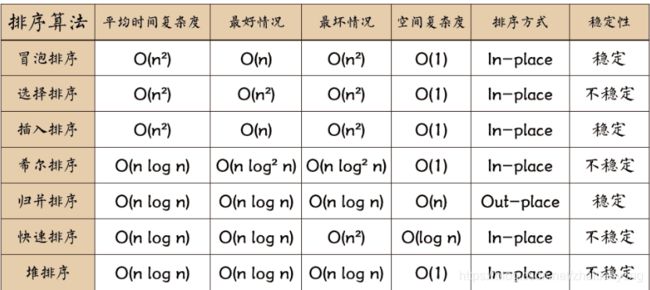
常用排序算法C++

冒泡排序

冒泡排序是比较简单的O(n2)级别的排序算法，思路是挨个比较邻近的数值，然后交换位置，就像在水里的泡泡一样，总能把最大的或者最小的交换到最上层。

/**
 * 冒泡排序
 */
template<typename T>
void bubble_sort(T arr[], int length)
{
     
    for (int i=0; i< length-1; i++){
     

        for(int j=0; j< length-1-i; j++){
     
            if (arr[j] > arr[j+1]){
     
                swap(arr[j], arr[j+1]);
            }
        }

    }
}

选择排序

选择排序的算法级别也是O(n2)，思路是从第一个索引开始，与剩下的进行比较，并记录最下的值的索引，依次比较下去。如果当前索引和初始的索引不同，那么需要交换值。此时最小的元素排在了前面。然后依次类推。

/**
 *选择排序
 */
template<typename T>
void select_sort(T arr[], int length){
     
    for (int i=0; i<length-1; i++){
     
        int minIndex = i;
        for(int j = i+1; j<length; j++){
     
            if(arr[minIndex] > arr[j]){
     
                minIndex = j;
            }
        }
        if(minIndex!=i){
     
            swap(arr[i], arr[minIndex]);
        }
    }
}

插入排序

插入排序，假设前面的数据是排列完整的，那么需要把当前的值与它前面的依次比较，直到遇到大于的位置，然后插入到其中。一般实现的时候可以选择依次交换位置，也可以进行赋值。
具体实现如下：

/**
 * 插入排序  交换数值
 */
template <typename T>
void insert_sort(T arr[], int length){
     
    for(int i=0; i< length -1; i++){
     
        for (int j = i+1; j>0 && (arr[j-1] > arr[j]); j--){
     
            //if (arr[j-1] > arr[j]){
     
                swap(arr[j-1], arr[j]);
           // }
        }
    }
}

可以对其进行优化，不需要每次都进行交换邻近，这样势必会浪费空间和时间，可以赋值操作

template <typename T>
void insert_sort2(T arr[], int length){
     
    for(int i=1; i< length; i++){
     
        T val = arr[i]; // 当前元素的值
        int j;
        for(j=i; j>0 && val < arr[j-1]; j--){
     
            arr[j] = arr[j-1]; // 向前移动
        }
        if(j!=i){
     
            arr[j] = val;
        }
    }
}

从代码中也可以看出，插入排序对大部分排好的序列是很快的。

希尔排序

插入排序是采用1步长进行排序的，而希尔排序在插入排序的基础上，先采用大步长，只到1步长为止，思想从整体上使得序列基本有序。

/**
 *希尔排序
 *
 */
template <typename T>
void shell_sort(T arr[], int length){
     
    int gap = 1;
    while (gap < length / 3) {
     
       gap = 3 * gap + 1;
    }
    cout << "gap = " << gap << endl;
    // 间隔Gap 进行插入排序
    while (gap>0) {
     
    	// 这里其实就是插入排序，只是以gap为间隔进行排序
        for(int i = 0; i <length; i += gap){
     
            for(int j= i + gap; j > 0 && (arr[j] < arr[j-gap]); j -= gap){
     
                 swap(arr[j], arr[j-gap]);
            }
        }
        gap = gap/3;
    }
}

归并排序

就是不断的把一个数组，对半分成两份，只到最后不能再分，然后再向上进行排序合并，典型的递归的思想

/**
 *归并排序
 *  分为左右，然后排序，然后合并 开辟临时内存空间
 */
template <typename T>
void merge_sort(T arr[], int length){
     
    __merge_sort(arr, 0, length-1);
}

template <typename T>
void __merge_sort(T arr[], int l, int r){
     
    if (l >=r){
     
        return;
    }

    int mid = l + (r-l) /2;  //(r+l)/2;
    __merge_sort(arr, l, mid);
    __merge_sort(arr, mid+1, r);

    // [l, mid] [mid+1, r]
    T * aux = new T[r-l+1];
    for(int i=l; i<=r; i++){
     
        aux[i-l] = arr[i];
    }

    int i = l, j = mid+1;
    for(int k = l; k <= r; k++){
     
        if (i > mid){
     
            arr[k] = aux[j-l]; // 复制剩下的右半边
            j++;
        }else if (j > r){
     
            arr[k] = aux[i-l]; // 复制剩下的左半边
            i++;
        }else if(aux[i-l] < aux[j-l]){
     
            arr[k] = aux[i-l]; // 复制左半边
            i++;
        }
        else{
     
            arr[k] = aux[j-l]; // 复制右半边
            j++;
        }
    }

    delete[] aux;

}

快速排序

快速排序的思想也是分而治之，首选需要选择一个基本值，然后小于基本值的在数组的左半边，大于的在右半边，中间部分是基本值，然后依次在对基本值的左边递归，对右半边也递归。

/**
 *快速排序  需要选择基准的数据，默认第一个，也可以随机选择
 */
template<typename T>
void quick_sort(T arr[], int length){
     
    __quick_sort(arr, 0, length-1);
}

template<typename T>
void __quick_sort(T arr[], int l, int r){
     
    if(l >= r)
    {
     
        return;
    }
    int index = __partition(arr, l, r);
    __quick_sort(arr, l, index-1);
    __quick_sort(arr, index+1, r);

}
template <typename T>
int __partition(T arr[], int l, int r){
     
    // 从两端向内
    //int index = rand()%(r-l+1)+l;
    //swap(arr[l], arr[index]);
    T v = arr[l]; // 选择第一个为基准值，也可随机选择，然后交换再进行
    int i = l + 1, j = r;

    while( true ){
     
        // 注意这里的边界, arr[i] < v, 不能是arr[i] <= v
        while( i <= r && arr[i] < v )
            i ++;

        // 注意这里的边界, arr[j] > v, 不能是arr[j] >= v
        while( j >= l+1 && arr[j] > v )
            j --;

        if( i > j )
            break;

        swap( arr[i] , arr[j] );
        // 注意这里的交换完，需要都向前移动一位
        i ++;
        j --;
    }

    swap(arr[l], arr[j]);
    return j;

堆排序

首先要了解什么是堆，堆其实就是一个二叉树，分为大顶推和小顶推，由小到大排序，一般小顶推。小顶堆的父节点的值小于两个孩子节点的值。具体可以去看堆的定义，这里就不多说了。

/**
 * 对元素组的堆排序
 */
template<typename T>
void heap_sort(T arr[], int length){
     
	// 构建堆
    for(int i = (length-1)/2; i >= 0; i--){
     
        __siftDown(arr, length, i);
    }

    for(int i = length-1; i >= 0; i--){
     
        swap(arr[0], arr[i]);
        __siftDown(arr, i, 0);
    }
}
template<typename T>
void __siftDown(T arr[], int length, int k){
     

    while ( 2*k+1 < length) {
     

        int i = 2*k + 1;
        if(i+1<length && arr[i] < arr[i+1]){
     
            i ++;
        }

        if(arr[k] >= arr[i])
            break;

        swap(arr[k], arr[i]);

        k = i;
    }
}

参考：https://www.runoob.com/w3cnote/ten-sorting-algorithm.html