外部排序算法总结
目录
多路归并排序
基本思想
两两归并排序
多路归并排序
胜者树
败者树
败者树的建立与调整
败者树的java代码
败者树的效率
我们一般提到排序都是指内排序,比如快速排序,堆排序,归并排序等,所谓内排序就是可以在内存中完成的排序。RAM的访问速度大约是磁盘的25万倍,我们当然希望如果可以的话都是内排来完成。但对于大数据集来说,内存是远远不够的,这时候就涉及到外排序的知识了。
外部排序指的是大文件的排序,即待排序的记录存储在外存储器上,待排序的文件无法一次装入内存,需要在内存和外部存储器之间进行多次数据交换,以达到排序整个文件的目的。
多路归并排序
基本思想
外部排序最常用的算法是多路归并排序,即将原文件分解成多个能够一次性装人内存的部分,分别把每一部分调入内存完成排序。然后,对已经排序的子文件进行归并排序。
一般来说外排序分为两个步骤:预处理和合并排序。即首先根据内存的大小,将有n个记录的磁盘文件分批读入内存,采用有效的内存排序方法进行排序,将其预处理为若干个有序的子文件,这些有序子文件就是初始顺串,然后采用合并的方法将这些初始顺串逐趟合并成一个有序文件。
两两归并排序
假设有一个含10000 个记录的文件,首先通过10 次内部排序得到10 个初始归并段R1~R10 ,其中每一段都含1000 个记录。然后两两归并,直至得到一个有序文件为止
如R1与R2归并排序成R12,R3与R4排序成R34,再R12与R34排序从R1234
这种方法要归并排序多次,时间耗费多,不提倡
多路归并排序
由于多路归并,有k路,就要比较k-1次,所以有了减少比较次数的胜者树与败者树,而多路归并常用败者树
多路归并排序算法在常见数据结构书中都有涉及。从2路到多路(k路),增大k可以减少外存信息读写时间,但k个归并段中选取最小的记录需要比较k-1次, 为得到u个记录的一个有序段共需要(u-1)(k-1)次,若归并趟数为s次,那么对n个记录的文件进行外排时,内部归并过程中进行的总的比较次数为 s(n-1)(k-1),也即(向上取整)(logkm)(k-1)(n-1)=(向上取整)(log2m/log2k)(k-1)(n-1),而(k- 1)/log2k随k增而增因此内部归并时间随k增长而增长了,抵消了外存读写减少的时间,这样做不行,由此引出了“败者树”tree of loser的使用。在内部归并过程中利用败者树将k个归并段中选取最小记录比较的次数降为(向上取整)(log2k)次使总比较次数为(向上取整) (log2m)(n-1),与k无关。
败者树是完全二叉树, 因此数据结构可以采用一维数组。其元素个数为k个叶子结点、k-1个比较结点、1个冠军结点共2k个。ls[0]为冠军结点,ls[1]--ls[k- 1]为比较结点,ls[k]--ls[2k-1]为叶子结点(同时用另外一个指针索引b[0]--b[k-1]指向)。另外bk为一个附加的辅助空间,不 属于败者树,初始化时存着MINKEY的值。
多路归并排序算法的过程大致为:
1):首先将k个归并段中的首元素关键字依次存入b[0]--b[k-1]的叶子结点空间里,然后调用CreateLoserTree创建败者树,创建完毕之后最小的关键字下标(即所在归并段的序号)便被存入ls[0]中。然后不断循环:
2)把ls[0]所存最小关键字来自于哪个归并段的序号得到为q,将该归并段的首元素输出到有序归并段里,然后把下一个元素关键字放入上一个元素本来所 在的叶子结点b[q]中,调用Adjust顺着b[q]这个叶子结点往上调整败者树直到新的最小的关键字被选出来,其下标同样存在ls[0]中。循环这个 操作过程直至所有元素被写到有序归并段里。
伪代码如下:
void Adjust(LoserTree &ls, int s)
/*从叶子结点b[s]到根结点的父结点ls[0]调整败者树*/
{ int t, temp;
t=(s+K)/2; /*t为b[s]的父结点在败者树中的下标,K是归并段的个数*/
while(t>0) /*若没有到达树根,则继续*/
{ if(b[s]>b[ls[t]]) /*与父结点指示的数据进行比较*/
{ /*ls[t]记录败者所在的段号,s指示新的胜者,胜者将去参加更上一层的比较*/
temp=s;
s=ls[t];
ls[t]=temp;
}
t=t/2; /*向树根退一层,找到父结点*/
}
ls[0]=s; /*ls[0]记录本趟最小关键字所在的段号*/
}
void K_merge( int ls[K])
/*ls[0]~ls[k-1]是败者树的内部比较结点。b[0]~b[k-1]分别存储k个初始归并段的当前记录*/
/*函数Get_next(i)用于从第i个归并段读取并返回当前记录*/
{ int b[K+1),i,q;
for(i=0; i=0 ; i--) /*依次从b[K-1]……b[0]出发调整败者*/
Adjust(ls , i); /*败者树创建完毕,最小关键字序号存入ls[0]
while(b[ls[0]] !=MAXKEY )
{ q=ls[0]; /*q为当前最小关键字所在的归并段*/
prinftf("%d",b[q]);
b[q]=Get_next(q);
Adjust(ls,q); /*q为调整败者树后,选择新的最小关键字*/
}
} 胜者树
胜者树的一个优点是,如果一个选手的值改变了,可以很容易地修改这棵胜者树。只需要沿着从该结点到根结点的路径修改这棵二叉树,而不必改变其他比赛的结果。
注意:方块,表示最底层要比较的东西,里面的值是要比较的数值,下面的是数值对应的index。
圆圈,表示节点与节点之间比较的结果,里面的值是比较后结果,对应的对象的index,这里是胜利的数的index,旁边的是这个圆圈对应的index。
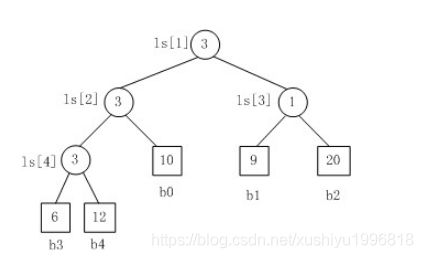
Fig.1是一个胜者树的示例。规定数值小者胜。
1. b3 PK b4,b3胜b4负,内部结点ls[4]的值为3;
2. b3 PK b0,b3胜b0负,内部结点ls[2]的值为3;
3. b1 PK b2,b1胜b2负,内部结点ls[3]的值为1;
4. b3 PK b1,b3胜b1负,内部结点ls[1]的值为3。.
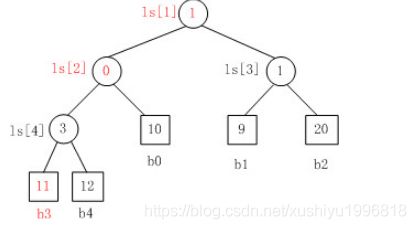
当叶子结点b3的值变为11时,重构的胜者树所示。
1. b3 PK b4,b3胜b4负,内部结点ls[4]的值为3;
2. b3 PK b0,b0胜b3负,内部结点ls[2]的值为0
3. b1 PK b2,b1胜b2负,内部结点ls[3]的值为1;
4. b0 PK b1,b1胜b0负,内部结点ls[1]的值为1。.
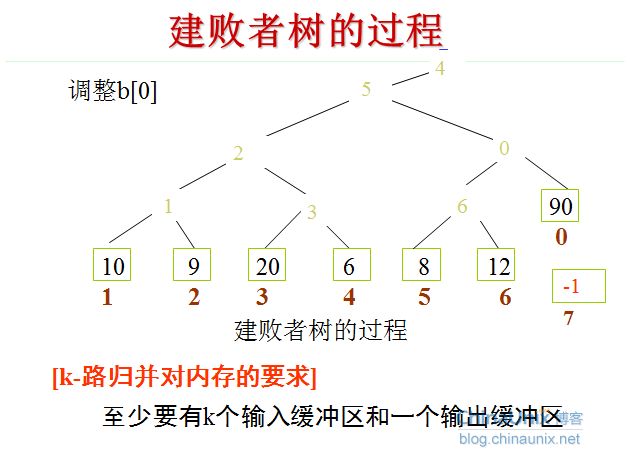
败者树
败者树是胜者树的一种变体。在败者树中,用父结点记录其左右子结点进行比赛的败者,而让胜者参加下一轮的比赛。败者树的根结点记录的是败者,需要加一个结点来记录整个比赛的胜利者。采用败者树可以简化重构的过程。
注意:方块,表示最底层要比较的东西,里面的值是要比较的数值,下面的是数值对应的index。
圆圈,表示节点与节点之间比较的结果,里面的值是比较后结果,对应的对象的index,这里是失败的数的index,旁边的是这个圆圈对应的index。
线段上的数字,表示线段下面的圆圈,对应的比较,胜利的数的index。
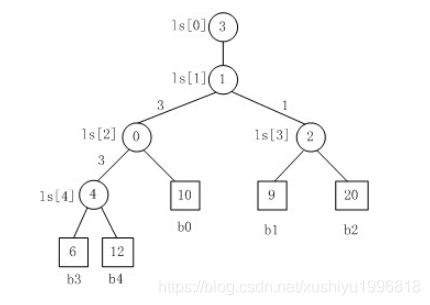
一棵败者树。规定数大者败。
1. b3 PK b4,b3胜b4负,内部结点ls[4]的值为4;
2. b3 PK b0,b3胜b0负,内部结点ls[2]的值为0;
3. b1 PK b2,b1胜b2负,内部结点ls[3]的值为2;
4. b3 PK b1,b3胜b1负,内部结点ls[1]的值为1;
5. 在根结点ls[1]上又加了一个结点ls[0]=3,记录的最后的胜者。
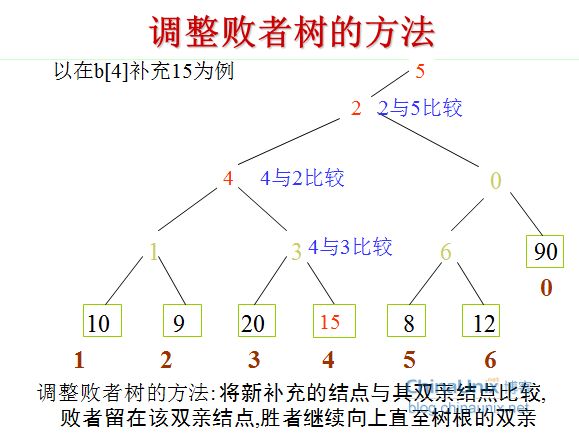
败者树重构过程如下:
将新进入选择树的结点与其父结点进行比赛:将败者存放在父结点中;而胜者再与上一级的父结点比较。
比赛沿着到根结点的路径不断进行,直到ls[1]处。把败者存放在结点ls[1]中,胜者存放在ls[0]中。
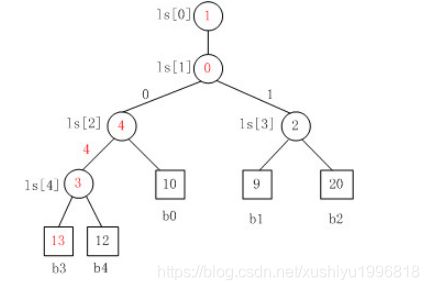
图是当b3变为13时,败者树的重构图。
注意,败者树的重构跟胜者树是不一样的,败者树的重构只需要与其父结点比较。对照Fig. 3来看,b3与结点ls[4]的原值比较,ls[4]中存放的原值是结点4,即b3与b4比较,b3负b4胜,则修改ls[4]的值为结点3。同理,以此类推,沿着根结点不断比赛,直至结束。
由上可知,败者树简化了重构。败者树的重构只是与该结点的父结点的记录有关,而胜者树的重构还与该结点的兄弟结点有关。
算法的步骤是:每次从k个组中的首元素中选一个最小的数,加入到新组,这样每次都要比较k-1次,故
算法复杂度为O((n-1)*(k-1)),而如果使用败者树,可以在O(logk)的复杂度下得到最小的数,算法复杂
度将为O((n-1)*logk), 对于外部排序这种数据量超大的排序来说,这是一个不小的提高。
败者树的建立与调整
败者树的java代码
package algorithm.sort.losertreeSort;
import java.awt.Adjustable;
import java.util.ArrayList;
import java.util.Arrays;
/*
*/
import java.util.Iterator;
/**
* @author xusy
*
*/
import java.util.List;
public class LoserTree {
//数据源,为叶子节点提供数据,iterator里的是有序的数据,从小到大
private Iterator[] data;
//总共有几个数据源
private int size;
//叶子节点,数据源中具体的数据,一对一
private Integer[] leaves;
//非叶子节点,记录叶子节点的下标, 根据节点的值可以定位到叶子节点所指向的数据(就是图里画的败者树)
//nodes[0]为最小值的索引
private int[] nodes;
/**根据data,构建败者树
* @param data iterator里的是有序的数据,从小到大
*/
public LoserTree(List> data){
//因为iterator不能变成迭代器数组,只能变成迭代器列表
this.data=data.toArray(new Iterator[0]);
size=data.size();
leaves=new Integer[size];
nodes=new int[size];
//为叶子节点,leaves数组赋值
for(int i=0;i=0;i--){
adjust(i);
}
}
/**根据数据源data,设置leaves[i]的值,如果对应的data没有值了,就设置null
* @param i 位置
*/
public void setLeavesValueFromData(int i){
Iterator iterator=data[i];
if(iterator.hasNext()){
leaves[i]=iterator.next();
}
else{
leaves[i]=null;
}
}
/**比较leaves数组中位置为index1的元素是否小于index2的元素(因为是要得到小的)
* @param index1
* @param index2
* @return
*/
public boolean compareLeavesByIndex(int index1,int index2){
Integer value1=leaves[index1];
Integer value2=leaves[index2];
if(value1==null){
return false;
}
if(value2==null){
return true;
}
//当叶节点数据相等时比较分支索引是为了实现排序算法的稳定性
if(value1==value2){
return index10) {
//如果父节点小于当前值,败者为当前值,败者留在父亲节点,index变成父亲节点的值,相当于父亲节点与祖父节点继续比较
//如果父节点大于当前值,败者为父节点,父节点不变,继续与祖父节点比较
if(compareLeavesByIndex(nodes[parent], index)){
int temp=nodes[parent];
nodes[parent]=index;
index=temp;
}
//祖父节点的位置
parent=parent/2;
//一套流程下来,index成为胜者,小的
//parent放置着败者,大的
//parent最后成为下一个比较的节点(祖父节点)
}
//跳出循环后,index成为最小的节点
nodes[0]=index;
}
/**返回败者树中data,经过败者树,多路归并排序后的list
* @return
*/
public List mergeSort(){
List list=new ArrayList<>();
Integer smallest=null;
while (true) {
//得到最小值
smallest=leaves[nodes[0]];
if(smallest==null){
break;
}
list.add(smallest);
//由于leaves数组中的最小值,索引为nodes[0]的元素被拿走了,所以要重新读入一个
setLeavesValueFromData(nodes[0]);
// 根据新插入的叶子节点重新调整树
adjust(nodes[0]);
}
return list;
}
}
测试
package algorithm.sort.losertreeSort;
import java.util.ArrayList;
import java.util.Collections;
import java.util.Iterator;
import java.util.List;
public class Main {
public static void main(String[] args) {
//int[][] testTable = {{1,2,3,0},{1,2,3,4},{1,2567678,3,4,6767,45,12,345,3435,34,66666},
//{1,1,1,3,3,4,3,2,4,2},{1,6,2,7,1}};
List> list=new ArrayList<>();
list.add(createRandomIntArray(-100,100,50));
list.add(createRandomIntArray(-100,100,40));
list.add(createRandomIntArray(-100,100,50));
list.add(createRandomIntArray(-100,100,50));
test(list);
}
private static void test(List> ito) {
//开始时打印数组
long begin = System.currentTimeMillis();
LoserTree tree=new LoserTree(ito);
List result=tree.mergeSort();
long end = System.currentTimeMillis();
//System.out.println(ito + ": rtn=" +rtn);
for (int i = 0; i < result.size(); i++) {
System.out.print(result.get(i)+" ");
}//打印结果几数组
System.out.println();
System.out.println("耗时:" + (end - begin) + "ms");
System.out.println("-------------------");
System.out.println("-------------------");
}
public static Iterator createRandomIntArray(int min,int max,int length){
List result=new ArrayList<>(length);
for(int i=0;i 败者树的效率
败者树可以在log(n)的时间内找到最值。任何一个叶子结点的值改变后,利用中间结点的信息,还是能够在log(n)的时间内找到最值。(n为多路归并的路数)
设,总共有k组,总共n个数据,每组n/k个
一开始对每组进行排序的时间是 k*log(n/k)*n/k=n*log(n/k)
进行败者树归并排序的时间为n*log(k)
总共时间为n*(log(n/k)+log(k))=n*log(n) 也就是最好的速度,速度为O(n*log(n))
所需的空间为O(k)