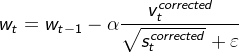几种优化算法的比较（BGD、SGD、MBGD、指数加权平均、momentum、NAG、RMSprop、Adam）

对于神经网络而言，初始化参数不是全0而是随机是非常重要的：假设神经网络的前一层输出的维度是m，经过当前层之后输出维度是n，那么当前层的参数初始化如下：

w=np.random.randn(m,n)*0.01 一般权重矩阵初始化比较小，He初始化：np.random.randn(m,n)*np.sqrt(2/n)

b=np.zeros((m,1))  一般偏差初始化为0

几种优化算法

下面主要讲解BGD、SGD、MBGD、momentum、指数加权平均、RMSprop、Adam、NGD

学习率是

全部框架是梯度下降法：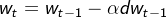

 

BGD(batch gradient descent)

算法：

特点：采用整个训练集的数据来计算 cost function 对参数的梯度，当数据集小于2000时（小数据集）使用。全局最优解；易于并行实现。从迭代的次数上来看，BGD迭代的次数相对较少。

缺点：由于这种方法是在一次更新中，就对整个数据集计算梯度，所以计算起来非常慢，遇到很大量的数据集也会非常棘手，而且不能接收新数据时更新模型。

SGD（stochastic gradient descent）

算法：

特点：每次更新时对每个样本进行梯度更新。训练速度比较快，并且可以新增样本。SGD伴随的一个问题是噪音较BGD要多，使得SGD并不是每次迭代都向着整体最优化方向。

缺点：准确度下降，并不是全局最优；不易于并行实现。 SGD 因为更新比较频繁，会造成 cost function 有严重的震荡。BGD 可以收敛到局部极小值，当然 SGD 的震荡可能会跳到更好的局部极小值处。当我们稍微减小 learning rate，SGD 和 BGD 的收敛性是一样的。

MBGD（mini-batch gradient descent）

算法：

特点：每次更新时对一批样本进行梯度更新。这样它可以降低参数更新时的方差，收敛更稳定，另一方面可以充分地利用深度学习库中高度优化的矩阵操作来进行更有效的梯度计算。当数据集大于2000使用

初衷：上面两种算法的均衡，算法的训练过程比较快，而且也要保证最终参数训练的准确率

缺点：不能保证很好的收敛性

指数加权平均（exponentially weighted average）

如果是用每一天的温度，第一天温度：，第二天温度：，第三天温度：，......

初始化，

表示温度的局部平均值，比如说第一天的平均温度是,第二天的平均温度是，......。那么每一天对应的平均温度画出来的图形就能描述温度的变化趋势

特点：来计算局部的平均值，来描述数值的变化趋势

偏差修正：我们可以知道v1和x1还是有很大的差距，不能反映实际情况；所以要使用偏差修正，偏差修正的主要目的是为了提高指数加权平均的精确度，主要是针对前期的加权平均值的计算精度。

      随着t的增大，分母趋向于1，对于后期没什么影响；如果对于前期的局部平均值精度没有什么要求，可以不修正

Momentum（动量梯度）

算法：对梯度进行动量

初始化：

NAG（Nesterov Accelerate Gradient）

初始化：

特点：初始位置（第一项），按照原来的更新方向更新一步（最后一项），然后在该位置计算梯度值（中间项），则在计算梯度时，不是在当前位置，而是新的位置上。比动量法更快的到达收敛点。

RMSprop（root mean square prop）均方根

只是对梯度的系数进行变化

  ε 是为了防止分母为0，通常取 1e−6

初始化：，β 默认值设为 0.9，学习率 α 默认值设为 0.001

 

Adam（Adaptive Moment Estimation）

就是在 RMSprop 的基础上加了 bias-correction 和 momentum

  

    偏差修正使得计算更加准确

几个参数推荐的默认值分别为：α=0.001，β1=0.9，β2=0.999，ε=10−8。t 是迭代次数，每个mini-batch后，都要进行 t += 1。

特点：Kingma et al表明带偏差修正的Adam算法稍微好于RMSprop。总之，Adam算法是一个相当好的选择，通常会得到比较好的效果。但是RMSprop的梯度是不带动量的算法。